
1.已知集合M={x|-1<x<2},N={y|y= x2-1,x∈M},则M∩N为
x2-1,x∈M},则M∩N为
A.{a|-1≤a<2} B.{a|-1<a<2}
C.{a|-1<a<1} D.
解析:y= x2-1,x∈(-1,2).
x2-1,x∈(-1,2).
所以y∈[-1,1).
答案:C
2.设x、y∈R,那么|x|<1且|y|<1是0<xy<1成立的____________条件.
A.充分不必要 B.必要不充分
C.充要 D.既不充分也不必要
解析:设x=- ,y=0,则xy=0.不能推出0<xy<1;
,y=0,则xy=0.不能推出0<xy<1;
设x=2,y=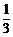 满足0<xy<1,不能推出|x|<1且|y|<1.
满足0<xy<1,不能推出|x|<1且|y|<1.
答案:D
3.不等式(x+1)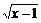 ≥0的解集是
≥0的解集是
A.{x|x>1} B.{x|x≥1}
C.{x|x≥1或x=-1} D.{x|x≥-1或x=1}
解析:∵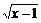 ≥0,∴x≥1.
≥0,∴x≥1.
又∵x+1=0,不等式成立.∴x=-1.选C.
答案:C
4.已知方程x2+(m+2)x+m+5=0有两个正实根,则实数m的取值范围是
A.m<-2 B.m≤-4
C.m>-5 D.-5<m≤-4
解析: -5<m≤-4.
-5<m≤-4.
答案:D
5.已知函数y=lg(x2-2kx+k)的值域为R,则k的取值范围是
A.0<k<1 B.0≤k≤1
C.k≤0或k≥1 D.k=0或k≥1
解析:Δ≥0 k≥1或k≤0.
k≥1或k≤0.
答案:C
6.x、y∈R,x2+y2=1,那么(1-xy)(1+xy)有
A.最小值 和最大值1 B.最小值
和最大值1 B.最小值 和最大值1
和最大值1
C.最小值 无最大值 D.最小值
无最大值 D.最小值 无最大值
无最大值
解析:令x=cosθ,y=sinθ,
则(1-xy)(1+xy)=1-x2y2=1- sin22θ.
sin22θ.
∵0≤sin22θ≤1,∴ ≤1-
≤1- sin22θ≤1.
sin22θ≤1.
答案:A
7.当x∈R+时,下列函数中,最小值为2的是
A.y=x2-2x+4
B.y=x+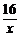
C.y=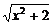 +
+
D.y=x+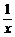
解析:y=x2-2x+4=(x-1)2+3≥3,
y=x+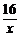 ≥8,y=
≥8,y=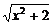 +
+ .
.
∵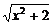 ≥
≥ ,∴y>2.故选D.
,∴y>2.故选D.
答案:D
8.已知a2<x<a,M=logax2,N=loga(logax),P=(logax)2,则
A.M>N>P B.P>M>N
C.M>P>N D.N>M>P
解析:∵a2<a,∴0<x<a<1.
∴logax>1,N=loga(logax)<0,
2logax>logax.logax,即M>P.
∴M>P>N.
答案:C
9.已知f(x)=ax,g(x)=bx,当f(x1)=g(x2)=3时,x1>x2,则a与b的大小关系不可能成立的是
A.b>a>1 B.a>1>b>0
C.0<a<b<1 D.b>1>a>0
解析:x1=loga3,x2=logb3.
当b>1>a>0时,x1<0,x2>0与x1>x2矛盾.选D.
答案:D
10.已知函数f(x)、g(x)(x∈R),设不等式|f(x)|+|g(x)|<a(a>0)的解集是M,不等式|f(x)+g(x)|<a(a>0)的解集是N,则
A.N M B.M=N C.M
M B.M=N C.M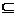 N D.M
N D.M N
N
解析:任取x0∈M,则|f(x0)+g(x0)|≤|f(x0)|+|g(x0)|<a.
∴x0∈N.但任取x1∈N,有
|f(x1)+g(x1)|<a,得不到|f(x1)|+|g(x1)|<a.
故M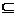 N.选C.
N.选C.
答案:C
11.某工厂第一年年产量为A,第二年的增长率为a,第三年的增长率为b,这两年的平均增长率为x,则
A.x=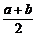 B.x≤
B.x≤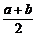
C.x>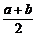 D.x≥
D.x≥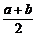
解析:A(1+x)2=A(1+a)(1+b),
∴(1+x)2≤( )2.
)2.
∴1+x≤1+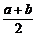 ,x≤
,x≤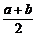 .
.
答案:B
12.线段|AB|=4,M为AB的中点,动点P满足条件|PA|+|PB|=6,当P点在同一平面内运动时,|PM|的最大值M、最小值m分别是
A.M=4,m=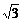 B.M=3,m=
B.M=3,m=
C.M=5,m= D.M=3,m=
D.M=3,m=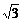
解析:P点轨迹是以A、B为焦点的椭圆,M是其中心,由解析几何知识知选B.
答案:B
13.若a、b∈R,且a+b+3=ab,则ab的取值范围是____________.
解析:ab≤(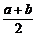 )2,∴a+b+3≤(
)2,∴a+b+3≤(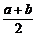 )2.
)2.
∴a+b≥6或a+b≤-2.
∴ab≥9或ab≤1.
答案:(-∞,1]∪[9,+∞)
14.若2x+4y=1,则x2+y2的最小值为____________.
解析:x2+y2=(-2y+ )2+y2
)2+y2
=5y2-2y+ =5(y-
=5(y- )2+
)2+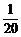 ≥
≥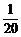 .
.
答案: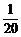
15.已知偶函数f(x)在[0,+∞)上为增函数,那么不等式f(x)>f(2-x)的解集是____________.
解析:∵f(x)为偶函数,则f(|x|)>f(|2-x|),
即|x|>|2-x|,得{x|x>1}.
答案:{x|x>1}
16.关于x的方程x2+(a2-1)x+a-2=0的两根满足(x1-1)(x2-1)<0,则a的取值范围是____________.
解析:(x1-1)(x2-1)<0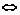 一根大于1,一根小于1.
一根大于1,一根小于1.
令f(x)=x2+(a2-1)x+a-2,则f(1)<0.
∴-2<a<1.
答案:-2<a<1
17.(12分)当|x-2|<a时,不等式|x2-4|<1成立,求正数a的取值范围.
解:由|x-2|<a,得2-a<x<2+a.
由|x2-4|<1,
得- <x<-
<x<-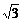 或
或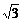 <x<
<x< .
.
∴(2-a,2+a)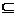 (-
(- ,-
,-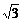 )∪(
)∪(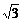 ,
, ).
).
∴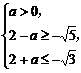 或
或
∴0<a< -2.
-2.
18.(12分)已知a、b、c为不等正数,且abc=1,求证: +
+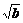 +
+ <
< +
+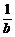 +
+ .
.
证明:结论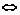
 +
+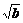 +
+ <bc+ac+ab
<bc+ac+ab
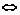 2
2 +2
+2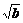 +2
+2 <2bc+2ac+2ab.
<2bc+2ac+2ab.
因为a、b、c为不等正数且abc=1,
所以bc+ac>2 =2
=2 .
.
ac+ab>2 ,ab+bc>2
,ab+bc>2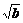 .
.
所以2 +2
+2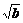 +2
+2 <2bc+2ac+2ab.
<2bc+2ac+2ab.
所以原不等式成立.
19.(12分)解不等式组 其中x、y都是整数.
其中x、y都是整数.
解:原不等式组可化为
得- <y<2.
<y<2.
∴y=0或1.
当y=0时,
解得
当y=1时,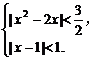 解得
解得
综上,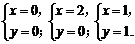
20.(12分)学校食堂定期从某粮店以每吨1500元的价格买大米,每次购进大米需支付运输劳务费100元,已知食堂每天需用大米1 t,贮存大米的费用为每吨每天2元,假定食堂每次均在用完大米的当天购买.
(1)该食堂每隔多少天购买一次大米,能使平均每天所支付的费用最少?
(2)粮店提出价格优惠条件:一次购买量不少于20 t时,大米价格可享受九五折优惠(即是原价的95%),问食堂可否接受此优惠条件?请说明理由.
解:设该食堂每隔x天购买一次大米,则每次购买x t,设每吨每天所支付的费用为y元,则
(1)y=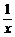 [1500x+100+2(1+2+…+x)]
[1500x+100+2(1+2+…+x)]
=x+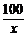 +1501≥1521,
+1501≥1521,
当且仅当x=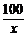 ,即x=10时取等号.
,即x=10时取等号.
故该食堂每隔10天购买一次大米,能使平均每天所支付的费用最少.
(2)y=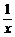 [1500x.0.95+100+2(1+2+…+x)](x≥20)
[1500x.0.95+100+2(1+2+…+x)](x≥20)
=x+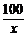 +1426,
+1426,
函数y在[20,+∞)上为增函数,
∴y≥20+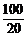 +1426=1451.
+1426=1451.
而1451<1521,故食堂可接受粮店的优惠条件.
21.(12分)设二次函数f(x)=ax2+bx+c(a、b、c∈R且a≠0),若函数y=f(x)的图象与直线y=x和y=-x均无公共点.
(1)求证:4ac-b2>1;
(2)求证:对一切实数x,恒有|ax2+bx+c|> .
.
证明:(1)方程ax2+bx+c=x和ax2+bx+c=-x均无实根,
即
①+②得4ac-b2>1.
(2)由4ac-b2>1,知a(x+ )2与
)2与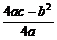 同号.
同号.
所以|ax2+bx+c|=|a(x+ )2+
)2+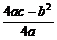 |
|
=|a(x+ )2|+|
)2|+|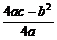 |≥|
|≥|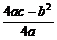 |>
|> .
.
22.(14分)已知二次函数f(x)=ax2+bx+c(a、b、c∈R,a>0),设方程f(x)=x的两个实数根为x1、x2.
(1)如果x1<2<x2<4,设f(x)的对称轴是x=x0,求证:x0>-1;
(2)如果|x1|<2,|x2-x1|=2,求b的取值范围.
(1)证明:设g(x)=f(x)-x=ax2+(b-1)x+1.
∴
x1<2<x2<4.∴(x1-2)(x2-2)<0,
即x1x2<2(x1+x2)-4.
于是x0=- =
= (-
(-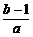 -
- )=
)= (x1+x2)-
(x1+x2)- x1x2>
x1x2> (x1+x2)-(x1+x2)+2=-
(x1+x2)-(x1+x2)+2=- (x1+x2)+2>-
(x1+x2)+2>- (2+4)+2=-1,即x0>-1.
(2+4)+2=-1,即x0>-1.
(2)解:由方程g(x)=ax2+(b-1)x+1=0,可知x1x2= >0,∴x1、x2同号.
>0,∴x1、x2同号.
若0<x1<2,则x2-x1=2,
∴x2=x1+2>2.g(2)=4a+2b-1<0. ①
又|x2-x1|2=(x1+x2)2-4x1x2=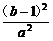 -
- =2.
=2.
∴2a+1= ,代入①式得
,代入①式得
2 <3-2b. ②
<3-2b. ②
解②得b< .
.
若-2<x1<0,则x2=-2+x1<-2.
∴g(-2)=4a-2b+3<0. ③
将2a+1= 代入③式得
代入③式得
2 <2b-1. ④
<2b-1. ④
解④得b>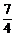 .
.
综上,可知b< 或b>
或b>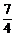 .
.
●意犹未尽
五枚金币
有个叫阿巴格的人生活在内蒙古草原上.有一次,年少的阿巴格和他爸爸在草原上迷了路,阿巴格又累又怕,到最后快走不动了.爸爸就从兜里掏出5枚硬币,把一枚硬币埋在草地里,把其余4枚放在阿巴格的手上,说:“人生有5枚金币,童年、少年、青年、中年、老年各有一枚,你现在才用了一枚,就是埋在草地里的那一枚,你不能把5枚都扔在草原里,你要一点点地用,每一次都用出不同来,这样才不枉人生一世.今天我们一定要走出草原,你将来也一定要走出草原.世界很大,人活着,就要多走些地方,多看看,不要让你的金币没有用就扔掉.”在父亲的鼓励下,那天阿巴格走出了草原.长大后,阿巴格离开了家乡,成了一名优秀的船长.
一语中的:珍惜生命,就能走出挫折的沼泽地.