
1.若 且
且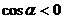 ,则
,则 是 ( )
是 ( )
A.第二象限角 B.第一或第三象限角
C.第三象限角 D.第二或第四象限角
2.给出两个命题: :
: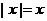 的充要条件是
的充要条件是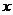 为正实数;
为正实数; :不等式
:不等式 取等号的条件是
取等号的条件是 异号,则下列哪个复合命题是真命题 ( )
异号,则下列哪个复合命题是真命题 ( )
A.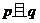 B.
B. C.
C. D.
D.
3.设等差数列 的公差为2,前
的公差为2,前 项和为
项和为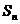 ,则下列结论中正确的是 ( )
,则下列结论中正确的是 ( )
A. B.
B.
C. D.
D.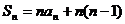
4.复数 的值等于 ( )
的值等于 ( )
A.1 B.-1 C.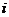 D.
D.
5.过点 作直线
作直线 与圆
与圆 交于A、B两点,如果
交于A、B两点,如果 ,则 ( )
,则 ( )
A. 的方程为
的方程为 ;
;
B. 的方程为
的方程为 ;
;
C. 的方程为
的方程为 ;
;
D. 的方程为
的方程为 ;
;
6.函数 的图象大致是 ( )
的图象大致是 ( )

A. B. C. D.
7.如果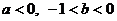 ,那么下列不等式中正确的是 ( )
,那么下列不等式中正确的是 ( )
A. B.
B.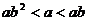 C.
C.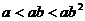 D.
D.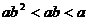
8.设函数 在
在 处连续,且
处连续,且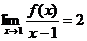 ,则
,则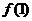 等于 ( )
等于 ( )
A. B.
B. C.
C.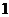 D.
D.
9.球面上有三点,其中任意两点的球面距离都等于球的大圆周长的 ,经过这三点的小圆的周长为
,经过这三点的小圆的周长为 ,则这个球的表面积为 ( )
,则这个球的表面积为 ( )
A. B.
B.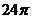 C.
C. D.
D.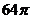
10.若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“同族函数”,那么函数解析式为 ,值域为
,值域为 的“同族函数”共有 ( )
的“同族函数”共有 ( )
A.7个 B.8个 C.9个 D.10个
11.6支签字笔与3本笔记本的金额之和大于24元,而4支签字笔与5本笔记本的金额之和小于22元,则2支签字笔与3本笔记本的金额比较结果是 ( )
A.3本笔记本贵 B.2支签字笔贵 C.相同 D.不确定
12. 如图,在
如图,在 中,
中,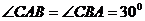 ,AC、BC边上的高分别为BD、AE,则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为 ( )
,AC、BC边上的高分别为BD、AE,则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为 ( )
A.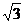 B.
B.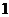
C. D.
D.
第Ⅱ卷(非选择题共90分)
13.已知A箱内有红球1个和白球5个,B箱内有白球3个,现随意从A箱中取出3个球放入B箱,充分搅匀后再从中随意取出3个球放入A箱,则红球由A箱移入到B箱,
 再返回到A箱的概率等于 .
再返回到A箱的概率等于 .
14.已知函数 是偶函数,
是偶函数, 是奇函数,
是奇函数,
它们的定义域是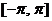 ,且它们在
,且它们在 上的
上的
 图象如图所示,则不等式
图象如图所示,则不等式 的解集
的解集
是 .
15.如图,在正方体ABCD-A1B1C1D1中,点M
是BC的中点,则D1B与AM所成角的余弦值
是 .
16. 如图,一条直角走廊宽为1.5m,一转动灵活的平
如图,一条直角走廊宽为1.5m,一转动灵活的平
板手推车,其平板面为矩形,宽为1m.问:要想
顺利通过直角走廊,平板手推车的长度不能超
过 米.
17.(本小题满分12分)甲、乙两名射手在一次射击中的得分为两个相互独立的随击变量 与
与 ,且
,且 、
、 的分布列为:
的分布列为:

(1)求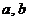 的值; (2)甲、乙两名射手在一次射击中的得分均小于3的概率谁大?
的值; (2)甲、乙两名射手在一次射击中的得分均小于3的概率谁大?
(3)计算 、
、 的期望和方差,并以此分析甲乙的技术状况.
的期望和方差,并以此分析甲乙的技术状况.
18.(本小题满分12分)已知函数 是定义在
是定义在 上的偶函数,当
上的偶函数,当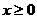 时,
时,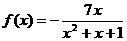 .
.
(1)求当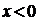 时
时 的解析式;
的解析式;
(2)试确定函数 的单调区间,并证明你的结论;
的单调区间,并证明你的结论;
(3)若 且
且 ,证明:
,证明: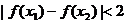 .
.
19.(本小题满分12分)在四棱锥 中,
中,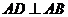 ,
, ,
,

 底面
底面 ,
,  ,直线
,直线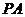 与底面
与底面
 成
成 角,点
角,点 分别是
分别是 的中点.
的中点.
(1)求二面角 的大小;
的大小;
(2)当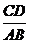 的值为多少时,
的值为多少时, 为直角三角形.
为直角三角形.
20.(本小题满分12分)已知在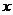 轴上有一点列:
轴上有一点列:
 ,点
,点 分有向线段
分有向线段 所成的比为
所成的比为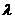 ,其中
,其中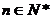 ,
,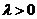 为
为
常数,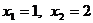 .
.
(1)设 ,求数列
,求数列 的通项公式;
的通项公式;
(2)设 ,当
,当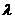 变化时,求
变化时,求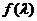 的取值范围.
的取值范围.
21. (本小题满分12分)在东西方向直线延伸的湖岸上有一港口O,一艘机艇以40km/h的速度从O港出发,先沿东偏北的某个方向直线前进到达A处,然后改向正北方向航行,总共航行30分钟因机器出现故障而停在湖里的P处,由于营救人员不知该机艇的最初航向及何时改变的航向,故无法确定机艇停泊的准确位置,试划定一个最佳的弓形营救区域(用图形表示),并说明你的理由.
(本小题满分12分)在东西方向直线延伸的湖岸上有一港口O,一艘机艇以40km/h的速度从O港出发,先沿东偏北的某个方向直线前进到达A处,然后改向正北方向航行,总共航行30分钟因机器出现故障而停在湖里的P处,由于营救人员不知该机艇的最初航向及何时改变的航向,故无法确定机艇停泊的准确位置,试划定一个最佳的弓形营救区域(用图形表示),并说明你的理由.
22.(本小题满分14分)如图,设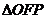 的面积为
的面积为 ,已知
,已知 .
.
(1)若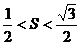 ,求向量
,求向量 与
与 的夹角
的夹角 的取值范围;
的取值范围;
(2)若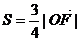 ,且
,且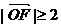 ,当
,当 取最小值时,建立适当的直角坐标系,求
取最小值时,建立适当的直角坐标系,求
 以
以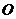 为中心,
为中心, 为一个焦点且经过点
为一个焦点且经过点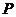 的椭圆方程.
的椭圆方程.
2005-2006学年度下学期 高中学生学科素质训练 高三第三轮数学综合测试(1) YCY 说明:本试卷分第一卷和第二卷两部分.第Ⅰ卷60分,第Ⅱ卷90分,共150分,答题时间120分钟. 参考公式: 三角函数的积化和差公式 正棱台、圆台的侧面积公式 其中、分别 表示上、下底面周长,表示斜高或母线长 球的参考答案
高三数学(一)参考答案
一、选择题
C D C A A D A B C C B A
提示:3。可理解为首项是 ,公差是
,公差是 的等差数列
的等差数列 ,故
,故
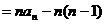
4.只要注意到 ,即可迅速得到答案.
,即可迅速得到答案.
5.此题可转化为求过点 的直线
的直线 ,
, 与圆
与圆 相交所得的弦长是否为
相交所得的弦长是否为 的问题.
的问题.
6. 应注意到函数 是奇函数, 可排除A,
B选项, 代数值
是奇函数, 可排除A,
B选项, 代数值 检验即得D.
检验即得D.
8. 特殊值法, 令 , 得
, 得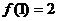 .
.
9. 由已知得小圆半径 ,
三点组成正三角形, 边长为球的半径
,
三点组成正三角形, 边长为球的半径 ,
所以有
,
所以有
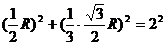 ,
, 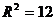 , 所以球的表面积
, 所以球的表面积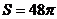 .
.
10.
由题意知同族函数的定义域非空,
且由 中的两个(这里
中的两个(这里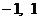 和
和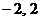 中各有一个), 或三个, 或全部元素组成, 故定义域的个数为
中各有一个), 或三个, 或全部元素组成, 故定义域的个数为 .
.
11. 设签字笔与笔记本的价格分别是 , 2支签字笔与3本笔记本的金额比较结果是
, 2支签字笔与3本笔记本的金额比较结果是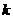 , 即
, 即
 ,已知
,已知 ,
, ,在直角坐标系中画图,可知直线
,在直角坐标系中画图,可知直线 的斜率始终为负, 故有
的斜率始终为负, 故有 , 所以选B.
, 所以选B.
12.
设 , 则在椭圆中, 有
, 则在椭圆中, 有 ,
,  ,
而在双曲线中, 有
,
而在双曲线中, 有
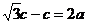 ,
,  ,
∴
,
∴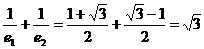 .
.
二、填空题13. 14.
14.  15.
15. 16.
16.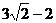
提示: 15. 设正方体的棱长为 , 过
, 过 点作直线
点作直线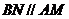 交
交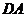 的延长线于
的延长线于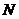 , 连
, 连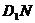 , 在
, 在 中,
中, 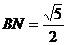 ,
, 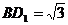 ,
,  , ∴
, ∴ 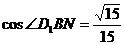 .
.
16. 设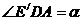 , 则有
, 则有 ,
,
根据小车的转动情况, 可大胆猜测只有 时,
时, 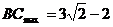 .
.
三、解答题
17.(1)∵ 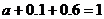 , ∴
, ∴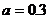 , 同理
, 同理 . -------3分
. -------3分
(2)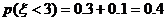 ,
,  ,
,
∴ -------------------3分
-------------------3分
(3)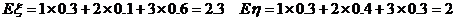 ----8分
----8分

同理  ----------10分
----------10分
 由计算结果
由计算结果 ,说明在一次射击中甲的平均得分比乙高,但
,说明在一次射击中甲的平均得分比乙高,但 ,
,
说明甲得分的稳定性比乙差,因而,甲乙两人的技术水平都不够全面. --------12分
18.(1)若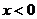 ,则
,则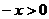 , ∵函数
, ∵函数 是定义在
是定义在 上的偶函数,
上的偶函数,
∴  ----------3分
----------3分
(2)当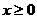 时,
时, . --------------6分
. --------------6分
显然当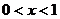 时,
时,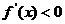 ;当
;当 时,
时, ,又
,又 在
在 和
和 处连续,
处连续,
∴函数 在
在 上为减函数,在
上为减函数,在 上为增函数. -----------8分
上为增函数. -----------8分
(3)∵函数 在
在 上为增函数,且
上为增函数,且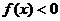 ,
,
∴当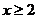 时,有
时,有 ,------------------10分
,------------------10分
又当 时,得
时,得 且
且 ,
即
,
即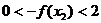
∴ 即得
即得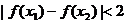 .
----------12分
.
----------12分
19.(1)由已知 , 得
, 得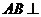 平面
平面 ,
,
又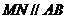 , ∴
, ∴ 平面
平面 ,
,

∴ 为二面角
为二面角 的平面角. ----------3分
的平面角. ----------3分
由已知 , 得
, 得 ,
,
∵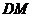 是
是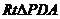 斜边
斜边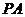 上的中线,
上的中线, 
∴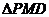 为等腰三角形,
为等腰三角形, 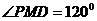 ,
,
即二面角 的大小为
的大小为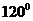 . -------------6分
. -------------6分
(2)显然 . 若
. 若 , 则
, 则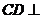 平面
平面 ,
,
而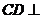 平面
平面 ,故平面
,故平面 与平面
与平面 重合,与题意不符.
重合,与题意不符.
由 是
是 ,则必有
,则必有 ,
,
连BD,设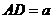 ,由已知得
,由已知得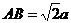 ,从而
,从而 ,
,
又 ,∴
,∴ ,得
,得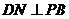 ,
,
故 平面
平面 ,
-----------8分
,
-----------8分
∴ ,又
,又 ,∴
,∴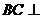 平面
平面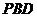 , ∴
, ∴ ,反之亦然.
,反之亦然.
∵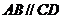 ∴
∴ 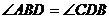 , ∴
, ∴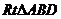 ∽
∽ -------10分
-------10分
∴ .
--------12分
.
--------12分
20.(1)由题意得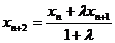 ,
,
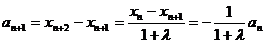 -----------3分
-----------3分
又 , ∴数列
, ∴数列 是首项为
是首项为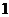 、公比为
、公比为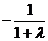 的等比数列,
的等比数列,
∴ --------------6分
--------------6分
(2)∵ ,
, 
∴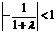 ,
,  ---------10分
---------10分
∴当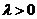 时,
时, 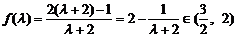 ------------12分
------------12分
21.以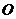 为原点,湖岸线为
为原点,湖岸线为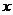 轴建立直角坐标系,
轴建立直角坐标系,
设OA的倾斜角为 ,点P的坐标为
,点P的坐标为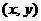 ,
,
 ,则有
,则有
 -------------6分
-------------6分
由此得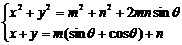
即 
故营救区域为直线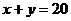 与圆
与圆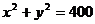 围城的弓形区域.(图略)--------12分
围城的弓形区域.(图略)--------12分
22.(1)由题意知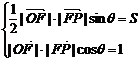 , 可得
, 可得 .
.
∵ ,
∴
,
∴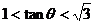 ,
有
,
有 . --------4分
. --------4分
(2)以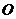 为原点,
为原点, 所在直线为
所在直线为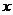 轴建立直角坐标系,
轴建立直角坐标系,
设 ,点
,点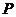 的坐标为
的坐标为 ,
,
∵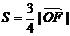 , ∴
, ∴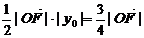 ,
,
 . -------6分
. -------6分
∴ ,
∴
,
∴ . ------8分
. ------8分
设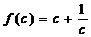 ,则当
,则当 时,有
时,有 .
.
∴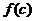 在
在 上增函数,∴当
上增函数,∴当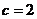 时,
时,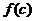 取得最小值
取得最小值 ,
,
从而 取得最小,此时
取得最小,此时 .
---------------------11分
.
---------------------11分
设椭圆方程为 ,
,
则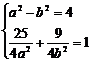 ,解之得
,解之得 ,故
,故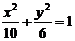 .--------14分
.--------14分