1.
若非空数集A = {x|2a + 1≤x≤3a-5 },B =
{x|3≤x≤22 },则能使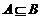 成立的所有a的集合是
A.{a|1≤a≤9} B.{a|6≤a≤9} C.{a|a≤9} D.
成立的所有a的集合是
A.{a|1≤a≤9} B.{a|6≤a≤9} C.{a|a≤9} D.
2. 已知二个不共线向量 ,且
,且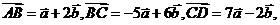 则一定共线的三点是
则一定共线的三点是
A. A、B、D B. A、B、C C. B、C、D D. A、C、D
3.已知函数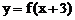 是偶函数, 则函数
是偶函数, 则函数 图象的对称轴为直线
图象的对称轴为直线
A.  B.
B.
 C.
C.
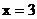 D.
D.
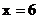
4.从原点向圆 x2+y2-12y+27=0作两条切线,则该圆夹在两条切线间的劣弧长为
A.π B.2π C.4π D.6π
5.命题p:若a、b∈R,则|a|+|b|>1是|a+b|>1的充分而不必要条件;命题q:函数
y= 的定义域是(-∞,-1
的定义域是(-∞,-1 ∪[3,+∞
∪[3,+∞ ,则
,则
A.“p或q”为假 B.“p且q”为真 C. p真q假 D. p假q真
6.若x,y是正数,则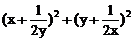 的最小值是
的最小值是
A.3 B.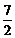 C.4 D.
C.4 D.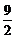
7.在R上定义运算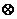 :
: .若不等式
.若不等式 对任意实数
对任意实数 成立,则
成立,则
A. B.
B. C.
C. D.
D.
8. 已知k<-4,则函数y=cos2x+k(cosx-1)的最小值是
(A) 1 (B) -1 (C) 2k+1 (D) -2k+1
9.设函数 为
为
A.周期函数,最小正周期为 B.周期函数,最小正周期为
B.周期函数,最小正周期为
C.周期函数,最小正周期为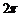 D.非周期函数
D.非周期函数
10.锐角三角形ABC中,a、b、c分别是三内角A、B、C的对边. 设B=2A,则 的取值范围是
的取值范围是
A.(-2,2) B.(0,2) C.(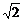 ,2) D.(
,2) D.( )
)
11.设 是函数
是函数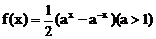 的反函数,则使
的反函数,则使 成立的
成立的 的取值范围为
的取值范围为
A. B.
B. C.
C. D.
D. 
12.经济学中的“蛛网理论”(如图),假定某种商品的“需求-价格”函数的图象为直线l1,“供给-价格”函数的图象为直线l2,它们的斜率分别为k1、k2,l1与l2的交点P为“供给-需求”均衡点,在供求两种力量的相互作用下,该商品的价格和产销量,沿平行于坐标轴的“蛛网”路径,箭头所指方向发展变化,最终能否达于均衡点P,与直线l1、 l2的斜率满足的条件有关,从下列三个图中可知最终能达于均衡点P的条件为
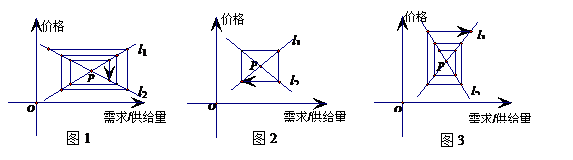
A.k1+k2>0 B.k1+k2=0 C.k1+k2<0 D.k1+k2可取任意实数
13.在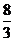 和
和 之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为___▲____.
之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为___▲____.
14.已知向量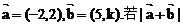 不超过5,则k的取值范围是
▲
.
不超过5,则k的取值范围是
▲
.
15. 已知 、
、 均为锐角,且
均为锐角,且 =
▲
.
=
▲
.
16. 若正整数m满足 ,则m = ▲ .
,则m = ▲ .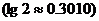
17.若函数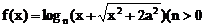 ,
, 是奇函数,则a= ▲ .
是奇函数,则a= ▲ .
18. 是正实数,设
是正实数,设 ,若对每个实数
,若对每个实数 ,
,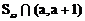 的元素不超过2个,且有
的元素不超过2个,且有 使
使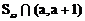 含2个元素,则
含2个元素,则 的取值范围是___▲ ___.
的取值范围是___▲ ___.
19.(本小题满分12分)设函数 ,求使f(x)≥2
,求使f(x)≥2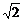 的x取值范围.
的x取值范围.
20. (本小题满分12分)已知△ABC的面积S满足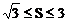 , 且
, 且 ,
,  与
与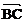 的夹角为
的夹角为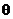 .
.
(I) 求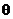 的取值范围;
的取值范围;
(II)求函数 的最小值.
的最小值.
21.(本小题满分14分)某公司生产的A型商品通过租赁柜台进入某商场销售,第一年商场为吸引厂家,决定免收该年的管理费,因此,该年A型商品定价为每件70元,销售量为11.8万件;第二年商场开始对该商品征收比率为p%的管理费(即每销售100元要征收p元),于是该商品的定价上升为每件 元,预计年销售量将减少p万件.
元,预计年销售量将减少p万件.
(Ⅰ)将第二年商场对商品征收的管理费y万元表示成p的函数,并指出这个函数的定义域;
(Ⅱ)要使第二年商场在此项经营中收取的管理费不少于14万元,则商场对该商品征收管理费的比率p%的范围是多少?
(Ⅲ)第二年,商场在所收管理费不少于14万元的前提下,要让厂家获得最大销售额,则p应为多少?
22.(本小题满分14分)设 是定义域为
是定义域为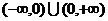 的奇函数,且它在区间
的奇函数,且它在区间 上是增函数.
上是增函数.
(I)用定义证明 在区间
在区间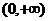 上是增函数;
上是增函数;
(II) 若 ,解关于
,解关于 的不等式:
的不等式: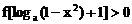 .(其中
.(其中 且
且 )
)
23.(本题满分14分) 对于函数  ,若存在
,若存在 ,使
,使
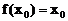 成立,
成立,
则称 为
为 的“滞点”.已知函数f ( x ) =
的“滞点”.已知函数f ( x ) =  .
.
(I)试问 有无“滞点”?若有,求之,否则说明理由;
有无“滞点”?若有,求之,否则说明理由;
(II)已知数列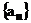 的各项均为负数,且满足
的各项均为负数,且满足 ,求数列
,求数列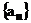 的通项公式;
的通项公式;
(III)已知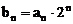 ,求
,求 的前项和
的前项和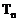 .
.
范水高级中学2005~2006年度第一学期高三数测试题
总分
13. 14.
15. 16.
17. 18.
|
19. (本小题满分12分) |
|
20. (本小题满分12分) 21. (本小题满分14分) 22. (本小题满分14分) 23. (本小题满分14分) |
范水高级中学2005~2006年度第一学期高三数测试题 模拟试卷 命题人:刘得华 责任人:华圆 (注意事项:本试卷满分150分,考试用时120分钟.请将答案写在答题卡上)参考答案
范水高级中学2005~2006年度第一学期高三数测试题数学试卷答案
一、选择题
1. B 2. A 3. C 4. B 5. D 6. C
7. C 8. A 9. B 10. D 11. A 12. A
二、填空题
13. 216 14.[-6,2] 15.
1 16. 155 17.  18.
18. 
三、解答题
19. 解:由于 在R上是增函数,所以,
在R上是增函数,所以, 等价于
等价于
 ①………………………………………(2分)
①………………………………………(2分)
(1)当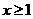 时,
时, ,所以①式恒成立. …………………(4分)
,所以①式恒成立. …………………(4分)
(2)当 时,
时,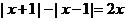 ,①式化为
,①式化为 ,即
,即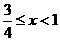 .…(8分)
.…(8分)
(2)当 时,
时, ,①式无解,……………………(10分)
,①式无解,……………………(10分)
综上, 的取值范围是
的取值范围是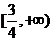 .…………………………………………(12分)
.…………………………………………(12分)
20. 解:(1)由题意知,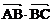

 , ………………①
, ………………①

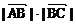
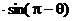

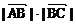
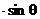 ,…………②………(2分)
,…………②………(2分)
由②÷①, 得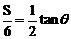 , 即
, 即
由 得
得 , 即
, 即 .……………(4分)
.……………(4分)
又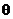 为
为 与
与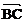 的夹角, ∴
的夹角, ∴ , ∴
, ∴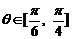 .……………(6分)
.……………(6分)
(2)
 ……………(9分)
……………(9分)
∵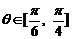 , ∴
, ∴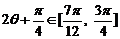 .……………(10分)
.……………(10分)
∴ , 即
, 即 时,
时,  的最小值为3. ……………(12分)
的最小值为3. ……………(12分)
21. 解:(1)依题意,第二年该商品年销售量为(11.8-p)万件,年销售收入为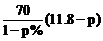 万元,
万元,
则商场该年对该商品征收的总管理费为 万元,……(2分)
万元,……(2分)
故所求函数为 .…………(4分)
.…………(4分)
由11.8-p>0及p>0得定义域为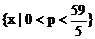 .…………(6分)
.…………(6分)
(2)由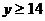 得
得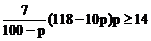 .…………(8分)
.…………(8分)
化简得 ,即
,即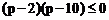 ,解得
,解得 .………(9分)
.………(9分)
故当比率在[2%,10%]内时,商场收取的管理费将不少于14万元. …………(10分)
(3)第二年,当商场的管理费不少于14万元时,厂家的销售收入为
 ,…………(12分)
,…………(12分)
因为 在区间
在区间 上为减函数,
上为减函数,
所以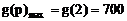 万元. …………(13分)
万元. …………(13分)
故当比率为2%时,厂家销售额最大,且商场收管理费又不少于14万元. ………(14分)
22. 解:(I)证明:在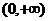 上任取两数
上任取两数 ,且
,且 ,
,
则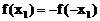 ,
,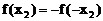 且
且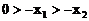 ,…………(2分)
,…………(2分)
∵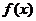 在
在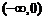 上是增函数,∴
上是增函数,∴ 即
即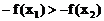 ,
,
∴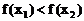 .
.
即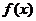 在区间
在区间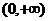 上是增函数. …………(4分)
上是增函数. …………(4分)
(II) ∵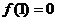 ,∴
,∴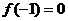 …………(6分)
…………(6分)
当 时,有
时,有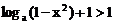 ,∴
,∴ ,…(8分)
,…(8分)
①
当 时,
时,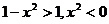 ,无解,…………(9分)
,无解,…………(9分)
当 时,
时,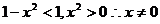 .…………(10分)
.…………(10分)
②
当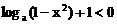 时,有
时,有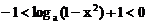 ,
,
即 .
.
当 时,
时,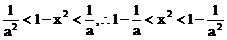 ,
,
∴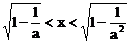 或
或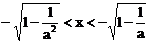 ;…………(12分)
;…………(12分)
当 时,
时,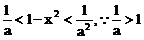 而
而 …………(13分)
…………(13分)
综上所述,当 时,原不等式的解集为
时,原不等式的解集为 且
且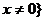
当 时,原不等式的解集为
时,原不等式的解集为
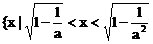 或
或 ………(14分)
………(14分)
23. 解:(I)由 令
令

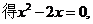 解得
解得
即f(x)存在两个滞点0和2 
(II)由题得 ,
, ①
①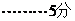
故 ②
②
由②-①得 ,
,
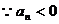
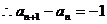 ,即
,即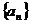 是等差数列,且
是等差数列,且

当n=1时,由


(III) ③
③
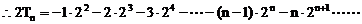 ④
④
由④-③得