
1.若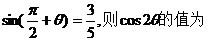 ( )
( )
A.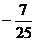 B.
B.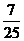 C.
C. D.
D.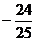
 2.如图所示,是一个正方体延棱剪开后的一种平面展开图,现在若沿其六个小正方形相邻边折叠,围成原来正方体,则②号正方形对面的正方形的编号是( )
2.如图所示,是一个正方体延棱剪开后的一种平面展开图,现在若沿其六个小正方形相邻边折叠,围成原来正方体,则②号正方形对面的正方形的编号是( )
A.⑥ B.⑤
C.④ D.③
3.复数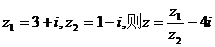 的模等于 ( )
的模等于 ( )
A.5 B. C.2 D.
C.2 D.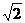
4.若a>1,则函数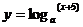 的图象不经过 ( )
的图象不经过 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.直线l绕它与x轴的交点逆时针旋转 ,得到直线
,得到直线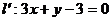 ,则直线l的方程为 ( )
,则直线l的方程为 ( )
A.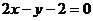 B.
B.
C. D.
D.
6.若 ,则正常数a、b的关系为 ( )
,则正常数a、b的关系为 ( )
A.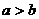 B.
B.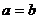
C.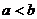 D.
D.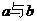 大小不定
大小不定
7.若一球的外切圆锥的高是这个球直径的2倍,则这个球的体积与其外切圆锥的体积的比为 ( )
A.1:2 B.1:3 C.2:3 D.3:4
8.顶点坐标为(1,-2),准线方程为 的抛物线的方程是 ( )
的抛物线的方程是 ( )
A. B.
B.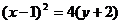
C. D.
D.
9.如果函数 ,那么 ( )
,那么 ( )
A.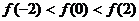 B.
B.
C. D.
D.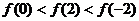
10.现有6个分乘两辆不同的车,每辆车最多乘4人,则不同的剩车方案数是 ( )
A.70 B.60 C.50 D.40
11.(理)E、F是正方体ABCD-A1B1C1D1的棱AB、C1D1的中点,A1B1所在直线过A1、E、C、F的截面所成的角的正切值为 ( )
A.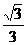 B.
B.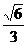 C.
C.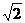 D.
D.
(文)E、F是正方体ABCD-A1B1C1D1的棱AB、C1D1的中点,异面直线A1E与B1C所成角的余弦值为 ( )
A. B.
B.
C.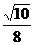 D.
D.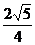
12.在△ABC中,ctgA是等差数列{an}的公差,且 是等比数列{bn}的公比,且
是等比数列{bn}的公比,且 ,则这个三角形是 ( )
,则这个三角形是 ( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.等腰三角形
第Ⅱ卷(非选择题,共90分)
13.(理)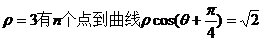 的距离等于
的距离等于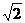 ,则n=
.
,则n=
.
(文)函数 则x的值为
.
则x的值为
.
14.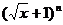 的展开式中,只有第六项的系数最大,则
的展开式中,只有第六项的系数最大,则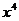 的系数是 .
的系数是 .
15.椭圆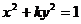 的两个焦点在圆
的两个焦点在圆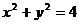 上,则此椭圆离心率e= .
上,则此椭圆离心率e= .
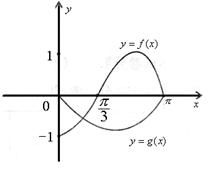 16.
16. 是奇函数,
是奇函数,
它们的定义域均为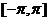 ,且它们在
,且它们在
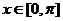 上的图象如图所示,则不等式
上的图象如图所示,则不等式
 .
.
17.(本小题满分12分)
已知函数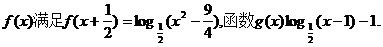
(Ⅰ)求函数f (x)的表达式;
(Ⅱ)若f (x)>g(x),求x的取值范围.
18.(本小题满分12分)
已知函数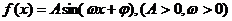 的图象如图所示.
的图象如图所示.
 (Ⅰ)求函数f (x)的解析式;
(Ⅰ)求函数f (x)的解析式;
(Ⅱ)令
19.(本小题满分12分)
如图,D、E分别是正三棱柱ABC-A1B1C1的棱AA1、B1C1的中点,且棱A1=4,AB=2.
(Ⅰ)求证:A1E//面BDC1;
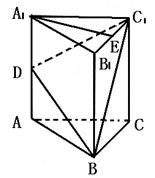 (Ⅱ)(理)在棱A1A所在直线上是否存在一点M,使二面角M-BC1-B1成60°.若存在,求出AM的长;若不存在,说明理由.
(Ⅱ)(理)在棱A1A所在直线上是否存在一点M,使二面角M-BC1-B1成60°.若存在,求出AM的长;若不存在,说明理由.
(文)求二面角A1-BC1-B1的正切值.
20.(本小题满分12分)
某农村在2003年底共有人口1480人,全年工农业生产总值为3180万元,从2004年起计划10年内该村的总产值每年增加60万元,人口每年净增a人.设从2004年起的第x年(2004年为第一年)该村人均产值为y万元.
(Ⅰ)写出y与x之间的函数关系式;
(Ⅱ)为使该村的人均产值年年都有增长,那么该村每年人口的净增量不能超过多少人?
21.(本小题满分12分)
已知双曲线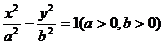 的一条渐近线方程为
的一条渐近线方程为 ,它的右焦点到右准线的距离为
,它的右焦点到右准线的距离为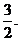
(Ⅰ)求双曲线方程;
(Ⅱ)在(Ⅰ)所求双曲线上存在关于直线 对称的两点,求实数k的范围.
对称的两点,求实数k的范围.
22.(本小题满分14分)
已知等比数列{xn}的各项为不等于1的正数,数列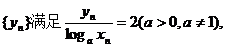
设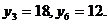
(Ⅰ)数列{yn}的前多少项和最大,最大值为多少?
(Ⅱ)试判断是否存在自然数m,使得当n>m时,xn>1恒成立.若存在,求出相应的m;若不存在,请说明理由.
(Ⅲ)令
陕西省高三教学质量检测试题 数 学 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分.考试时间120分钟. 正棱台、圆台的侧面积公式 S台侧= 其中、c分别表示上、下底面周长,l表示斜高或母线长 球体的体积公式 其中R表示球的半径. 参考公式: 三角函数的积化和差公式 第Ⅰ卷(选择题 共60分)参考答案
2004年陕西省高三教学质量检测试题
数学参考答案及评分标准
一、选择题
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
答案 |
A |
B |
B |
D |
A |
C |
A |
A |
D |
C |
理 |
C |
B |
|
文 |
B |
二、填空题
13.(理)4,(文)5
14.45
15. 16.
16.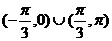
三、解答题(解答题只给出一种解法的评分标准,各题的其它正确解法可参照相应试题所给解法的评分标准赋分)
17.解:
(Ⅰ)
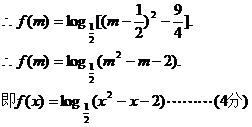
(Ⅱ)

18.解:
(Ⅰ)由图象可知,

(Ⅱ)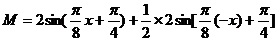

19.(Ⅰ)证明:如图,连结B1C交BC1于F,连结DE、DF.
则由题设可知:EF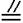
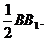
而A1D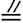
 ∴EF
∴EF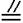 A1D
A1D
∴四边形A1DFE为平行四边形.
∴A1E//DF.又DF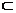 平面DBC1,A1E
平面DBC1,A1E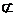 面DBC1,
面DBC1,
∴A1E//面DBC1.…………(5分)
|
(Ⅱ)(理)取BC的中点F,连结EF交BC1于点O,则O为BC1的中点.
过M作MN//A1E交OE于点N,则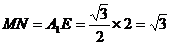 .
.
∵A1E⊥面B1BCC1,
∴MN⊥面B1BCC1.
∴过N作NR⊥BC1交BC1于R,连结MR,则∠MRN为二面角M-BC1-B1的平面角.(8分)
要使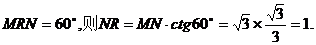
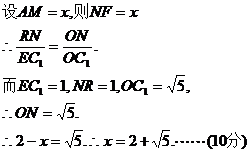
显然 说明点M在AA1的延长线上,同理,在A1A的延长线上也存在一点P,得
说明点M在AA1的延长线上,同理,在A1A的延长线上也存在一点P,得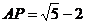 .
.
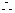 在A1A所在直线上存在点M,使二面角M-BC1-B1成60°.且AP=2+
在A1A所在直线上存在点M,使二面角M-BC1-B1成60°.且AP=2+ 或
或
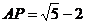 …………(12分)
…………(12分)
(文)如图(1),过E作EP⊥BC1,连结A1P.
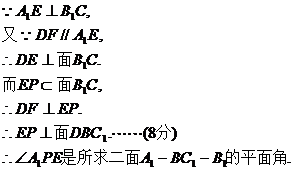
由题意知,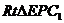 ∽
∽

(20)(Ⅰ)依题意知,第x年该村的工农业生产总值为(3180+60x)万元,该村第x年的人口总数(1480+ax)人.
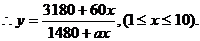 …………(5分)
…………(5分)
(Ⅱ)为使该村的人均产值年年都有增长,则在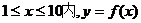 为增长函数,设
为增长函数,设



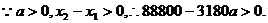 ……(11分)
……(11分)

|


由②可知, ……③…………(2分)
……③…………(2分)
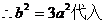 ③可得,
③可得,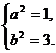
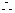 所求双曲线方程为
所求双曲线方程为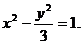 …………(4分)
…………(4分)
(Ⅱ)设与l垂直的直线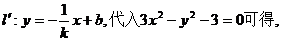
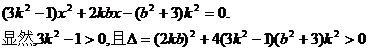
即 …………(8分)
…………(8分)
设线段AB的中点为M(x0,y0),则 …………(10分)
…………(10分)
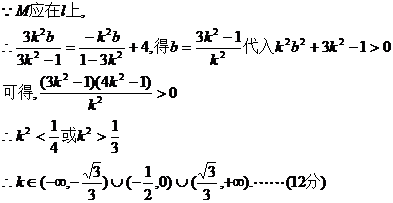
22.(Ⅰ)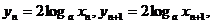
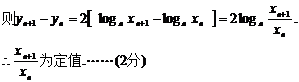
∴{xn}为等比数列.

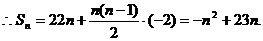
 且最大值为132.…………(6分)
且最大值为132.…………(6分)
(Ⅱ)
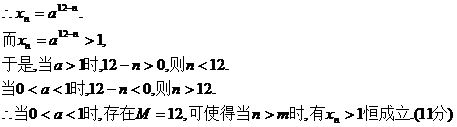
(Ⅲ)
 ……(14分)
……(14分)