
1.已知集合 ,
,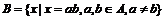 ,则集合B中的元素个数为
,则集合B中的元素个数为
A. 2 B. 3 C. 4 D. 5
2.与函数y=x相同的是
A.  B.
B.
 C.
C.
 D.
D.
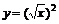
3.函数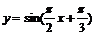 的最小正周期是
的最小正周期是
A. 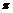 B.
B.
 C.4
D. 1
C.4
D. 1
4.函数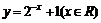 的反函数是
的反函数是
A. 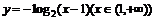 B.
B.

C. 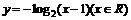 D.
D.
5.函数 的一个单调递减区间是
的一个单调递减区间是
A. 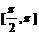 B.
B.
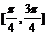 C.
C.
 D.
D.
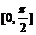
6.设A(1,2),B(4,2),若点A、B按向量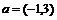 平移后对应点
平移后对应点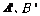 ,则
,则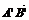 =
=
A. (2,3) B.(3,5) C.(3,0) D. (-4,3)
7.等比数列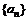 的前n项和为Sn,已知S4=1,S8=3,则
的前n项和为Sn,已知S4=1,S8=3,则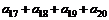 的值为
的值为
A. 32 B. 16 C. 8 D. 4
8.已知单位向量a、b,它们的夹角为 ,则
,则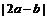 的值为
的值为
A. 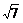 B.
-10
C. 10 D.
B.
-10
C. 10 D. 
9.已知函数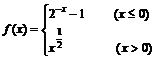 ,若
,若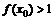 ,则x0的取值范围是
,则x0的取值范围是
A. (-1,1)
B. (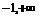 )
)
C.  D.
D.

10.在ΔABC中,角A、B、C所对边分别是a、b、c,且 ,则ΔABC的形状是
,则ΔABC的形状是
A. 等腰三角形或直角三角形 B. 直角三角形
C. 等腰直角三角形 D. 等腰三角形
11.定义在R上的偶数函数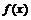 在
在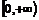 上是增函数,若
上是增函数,若 ,则适合不等式
,则适合不等式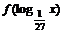 >0的x的取值范围是
>0的x的取值范围是
A.  B.
B.
 C.
C.
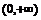 D.
D.
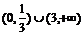
12.甲、乙两工厂2004年元月份的产值相等,甲厂的产值逐月增加且每月增加的数量相同,乙厂产值也逐月增加且每月的增长率相同,若2005年元月份两厂的产值又相等,则2004年7月份两厂的产值关系是
A. 甲厂的产值高 B. 乙厂的产值高
C. 甲厂、乙厂的产值相同 D. 无法确定
第Ⅱ卷(非选择题 共90分)
13.一个容量为20的样本,数据的分组及各组的频数如下:
(10,20],2;(20,30],3;(30,40],4;(40,50],5;(50,60],4;(60,70],2。则样本在区间(10,50]上的频率为 。
14.已知向量 与
与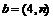 共线,则实数n=
。
共线,则实数n=
。
15.设数列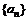 的前n项和Sn满足:
的前n项和Sn满足: ,则该数列的通项公式an= 。
,则该数列的通项公式an= 。
16.给出以下命题
①设 ,则
,则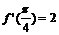 ;
;
②函数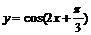 的图象的一条对称轴为
的图象的一条对称轴为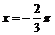 ;
;
③要得到函数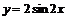 的图象只须将
的图象只须将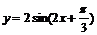 的图象向左平移
的图象向左平移 个单位长度。其中正确命题的序号是 。
个单位长度。其中正确命题的序号是 。
17.(本小题满分12分)
若A是锐角,向量 且
且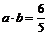 。
。
求tan2A的值。
18.(本小题满分12分)
已知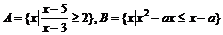 ,若
,若 ,求实数a的范围。
,求实数a的范围。
19.(本小题满分12分)
函数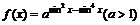 在[0,2
在[0,2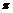 ]上的最大值为
]上的最大值为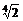 ,求实数a的值与函数f(x)取得最大值时的x集合。
,求实数a的值与函数f(x)取得最大值时的x集合。
20.(本小题12分)
2005年10月27日第十届全国人大常委第十八次会议通过了关于修改《中华人民共和国个人所得税法》的决定,修改后的《中华人民共和国个人所得税法》规定“个人工资、薪金等所得,以每月收入额减除费用一千六百元后的余额,为应纳税所得额。”修改后的个人所得率税率表为:
|
级数 |
全月应纳税所得额 |
税率% |
|
1 |
不超过500元的 |
5 |
|
2 |
超过500元至2000元的部份 |
10 |
|
3 |
超过2000元至5000元的部份 |
15 |
|
4 |
超过5000元至20000元的部份 |
20 |
|
… |
|
… |
(1)设个人的月工资、薪金等所得为x元( ),月纳税额为y元,写出y与x的函数关系式;
),月纳税额为y元,写出y与x的函数关系式;
(2)若某职员某月工资、薪金等所得为3300元,求该职员该月应纳税多少元?
21.(本小题满分12分)
已知函数 在x=2时有极值,其图象在点(1,f(1))处的切线与直线
在x=2时有极值,其图象在点(1,f(1))处的切线与直线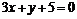 平行。
平行。
(1)求该函数的单调递减区间;
(2)当m>0时,求函数f(x)在[0,m]上的最小值。
22.(本小满分14分)
设等差数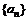 的前n项和为Sn,公差d >0,若
的前n项和为Sn,公差d >0,若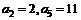 。
。
(1)求数列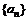 的通项公式;
的通项公式;
(2)设 ,若
,若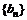 是等差数列,求实数a的值;
是等差数列,求实数a的值;
(3)在(1)(2)下,设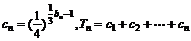 。是否存在正整数m、n,使
。是否存在正整数m、n,使 成立,若存在,求出m、n的值;若不存在,说明理由。
成立,若存在,求出m、n的值;若不存在,说明理由。
四川省泸州市高中2006级第一次诊断考试 数学(文史财经类) 本试题分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1至2页,第Ⅱ卷第3至8页。120分钟完卷,满分150分。 txjy 第Ⅰ卷(选择题,共60分) txjy 参考公式: 如果事件A、B互斥,那么P(A+B)=P(A)+P(B); 如果事件A、B相互独立,那么P(A•B)=P(A)•P(B); 如果事件A在一次试验中发生的概率为P,那么n次独立重复试验中恰好发生k次概率:。 txjy参考答案
四川省泸州市高中2006级第一次诊断考试参考答案及评分意见
数学(文)答案
一、选择题
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
C |
A |
C |
A |
D |
C |
B |
D |
D |
A |
D |
A |
二、填空题
13.
0.7 14.
±2
15. 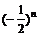 16. ①②
16. ①②
三、解答题
17. 解(1)∵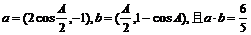
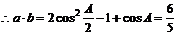 ,
2分
,
2分
 即cosA=
即cosA= 4分
4分
又 A是锐角,由
A是锐角,由 得:
得: 6分
6分
 8分
8分
 10分
10分
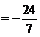 12分
12分
18.解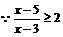 ,
,
 ,
2分
,
2分
故: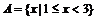 5分
5分
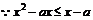
 6分
6分
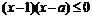 7分
7分
(1)当a<1时,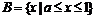 ;
;
则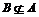 ;
8分
;
8分
(2)当a=1时,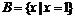 ;
;
则 ;
9分
;
9分
(3)当a>1时,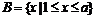 ;
;
要 ,则1<a<3;
11分
,则1<a<3;
11分
综上:符合条件的a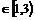 .
12分
.
12分
19. 解:
 2分
2分

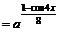 4分
4分
设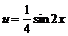 ,因
,因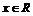 则
则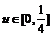
又函数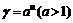 在
在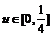 上是增函数,
上是增函数,
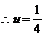 时,函数有最大值为
时,函数有最大值为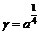 8分
8分
由已知得: 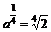 ,则
,则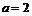 ,
10分
,
10分
又 ,则
,则 即
即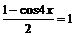 ,
,
故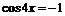 ,则
,则 .
.
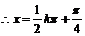 即函数取得最大值时的集合
即函数取得最大值时的集合 12分
12分
20. 解: (1)当0≤x≤1600时,y=0; 2分
当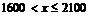 时,全月应纳税所得额为
时,全月应纳税所得额为 ,
,
则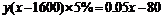 ;
4分
;
4分
当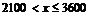 时,全月应纳税所得额为
时,全月应纳税所得额为 ,
,
则 6分
6分
故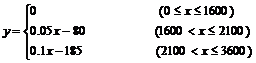 8分
8分
(2)当x=3300时,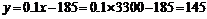 10分
10分
答:若某职员某月工资、薪金所得为3300元,该职员该月应纳税145元 12分
21. 解:(1)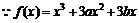
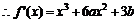
 在
在 时有极值则
时有极值则 时,
时,
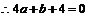 ①
4分
①
4分
∵图象上在横坐标为x=1处的点切线与直线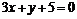 平行
平行
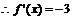 ,即
,即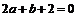 ②
6分
②
6分
由①②得:
 ,
,
设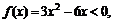 则
则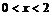
故该函数的单调区间是(0,2)。 8分
(2)由(1)知该函数在(0,2)是减函数,在(2,+∞)是增函数,
当 时,
时,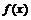 在[0,m]上是减函数,
在[0,m]上是减函数,
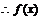 有最小值
有最小值 10分
10分
当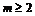 时,
时,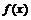 在[0,2]是减函数,[2,m]上是增函数,
在[0,2]是减函数,[2,m]上是增函数,
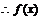 有最小值是f(2)=-4
12分
有最小值是f(2)=-4
12分
22. 解:(1)设等差数列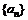 的通项为
的通项为 ,
,
由题得: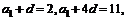 2分
2分
解得:
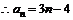 4分
4分
(2)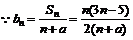 ,且
,且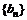 是等差数列;
是等差数列;
 ,故
,故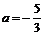 9分
9分
(3)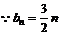

 10分
10分
由 ,得
,得 整理:
整理: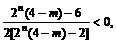
 12分
12分
假设 成立,由于2n是偶数,4-m是整数
成立,由于2n是偶数,4-m是整数
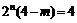
故
即
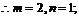 或
或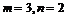 ,使
,使 成立
14分
成立
14分