
符合题目要求的)
1.给出下列函数:①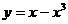 ,②
,②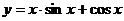 ,③
,③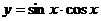 ,
,
④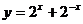 ,其中是偶函数的有 ( )
,其中是偶函数的有 ( )
A.1个 B.2个 C.3个 D.4个
2.若α、β终边关于y轴对称,则下列等式成立的是 ( )
A.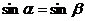 B.
B.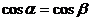 C.
C. D.
D.
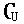 3.设全集U=R,
3.设全集U=R,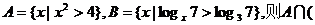 B)是 ( )
B)是 ( )
A. B.
B.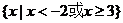
C. D.
D.
4.函数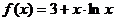 的单调递增区间是 ( )
的单调递增区间是 ( )
A. B.
B. C.
C.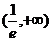 D.
D.
5.设等比数列 的前n项和为Sn,若
的前n项和为Sn,若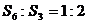 ,则
,则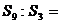 ( )
( )
A.1:2 B.2:3 C.3:4 D.1:3
6.若 ,则
,则
 的值是 ( )
的值是 ( )
A.1 B.-1 C.2 D.-2
7.在平面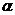 内的两条直线
内的两条直线 、
、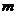 都平行于平面
都平行于平面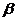 是平面
是平面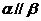 的 ( )
的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.不充分也不必要条件
8.把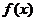 的反函数
的反函数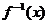 图象向右平移2个单位就得到曲线C,函数
图象向右平移2个单位就得到曲线C,函数 的图象与曲线
的图象与曲线
C关于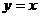 成轴对称,那么
成轴对称,那么 等于 ( )
等于 ( )
A.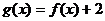 B.
B.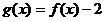
C.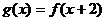 D.
D.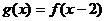
9.已知点A为双曲线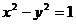 的顶点,点B和点C在双曲线的同一分支上,且A与B在y轴的异侧,则正△ABC的面积是 ( )
的顶点,点B和点C在双曲线的同一分支上,且A与B在y轴的异侧,则正△ABC的面积是 ( )
A.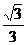 B.
B.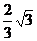 C.
C.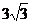 D.
D.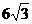
10.设坐标原点为O,抛物线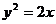 与过其焦点的直线交于两点A、B,则
与过其焦点的直线交于两点A、B,则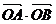 等于
等于
( )
A. B.
B. C.-3 D.3
C.-3 D.3
11.记函数 在区间[-2,2]上的最大值为M,最小值为m,那么M+m的
在区间[-2,2]上的最大值为M,最小值为m,那么M+m的
值为 ( )
A.0 B.3 C.6 D.8
12.13年前有一笔扶贫助学资金,每年的存款利息(年利率11.34%,不扣税)可以资助100
人上学,平均每人每月94.50元。现在(存款年利率1.98%,并且扣20%税)用同样一
笔资金每年的存款利息最多可以资助( )人上学(平均每人每月100元).
A.10 B.13 C.15 D.20
第Ⅱ卷(非选择题)
13.已知复数z满足等式: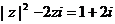 ,则z=
.
,则z=
.
14.某公司规定:一个工人在一个季度里如果有1个月完成任务,则可得奖金90元;如果
有2个月完成任务,则可得奖金210元;如果有3个月完成任务,则可得奖金330元;
如果3个月都未完成任务,则不得奖金。假如某工人每月能否完成任务是等可能的,则
这个在一个季度里所得奖金的数学期望是 。
15.某学校要从高三的6个班中派9名同学参加市中学生外语口语演讲,每班至少派1人,
则这9个名额的分配方案共有 种.(用数字作答)
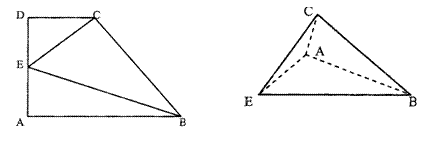
16.一直角梯形ABCD,AB⊥AD,AD⊥DC,AB=2,BC= ,CD=1,E为AD中点,沿
,CD=1,E为AD中点,沿
CE、BE把梯形折成四个面都是直角三角形的三棱锥,使点A、D重合,则这三棱锥的
体积等于 .
17.(本小题满分12分)在人寿保险业中,要重视某一年龄的投保人的死亡率,经过随机抽
样统计,得到某城市一个投保人能活到75岁的概率为0.60,试问:
(1)3个投保人都能活到75岁的概率;
(2)3个投保人中只有1人能活到75岁的概率;
(3)3个投保人中至少有1人能活到75岁的概率.(结果精确到0.01)
18.(本小题满分12分)已知向量 .
.
①若点A、B、C能构成三角形,求实数m应满足的条件;
②若△ABC为直角三角形,且∠A为直角,求实数m的值.
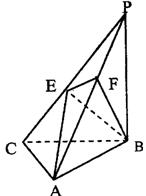
19.(本小题满分12分)已知三棱锥P-ABC中PB⊥底面ABC,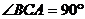 ,
,
PB=BC=CA=a,E是PC的中点,点F在PA上,且3PF=FA.
(1)求证:平面PAC⊥PBC;
(2)求平面BEF与底面ABC所成角(用一个反三角函数值表示).
20.(本小题满分12分)设 是由正数组成的无穷数列,Sn是它的前n项之和,对任意自
是由正数组成的无穷数列,Sn是它的前n项之和,对任意自
然数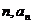 与2的等差中项等于Sn与2的等比中项.
与2的等差中项等于Sn与2的等比中项.
(1)写出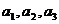 ;
;
(2)求数列的通项公式(要有推论过程);
(3)记 .
.
21.(本小题满分12分)设函数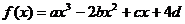 (a、b、c、d∈R)图象关于
(a、b、c、d∈R)图象关于
原点对称,且x=1时,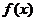 取极小值
取极小值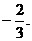
(1)求a、b、c、d的值;
(2)当 时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明
时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明
你的结论;
(3)若 时,求证:
时,求证: .
.
22.(本小题满分14分)已知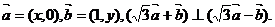
(1)求点 的轨迹C的方程;
的轨迹C的方程;
(2)若直线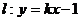 与曲线C交于A、B两点,并且A、B在y轴的同一侧,求实
与曲线C交于A、B两点,并且A、B在y轴的同一侧,求实
数k的取值范围.
(3)设曲线C与x轴的交点为M,若直线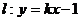 与曲线C交于A、B两点,是否
与曲线C交于A、B两点,是否
存在实数k,使得以AB为直径的圆恰好过点M?若有,求出k的值;若没有,写
出理由.
湖南师大附中高三第六次月考试卷 数 学(理科) 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),试题满分150分,考试时量120分钟。 第Ⅰ卷(选择题)参考答案
湖南师大附中高三第六次月考试卷
数学参考答案(理科)
一、选择题答案:
1.B 2.A 3.B 4.C 5.C 6.B 7.B 8.A 9.C 10.B 11.C 12.B
二、填空题答案:
13.-1,-1-2i
14.153.75元
15.56
16.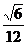
三、解答题
17.(1)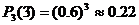
(2)
(3)
18.解①已知向量
若点A、B、C能构成三角形,则这三点不共线,………………2分
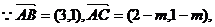 …………5分
故知
…………5分
故知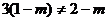 ……7分
……7分
∴实数 时,满足的条件…………8分
时,满足的条件…………8分
(若根据点A、B、C能构成三角形,必须|AB|+|BC|>|CA|…相应给分)
②若△ABC为直角三角形,且∠A为直角,则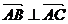 ,
,
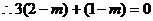 …………10分
解得
…………10分
解得 …………12分
…………12分
19.(1)证明:∵PB⊥底面ABC,∴PB⊥AC…………1分,又∠BCA=90°
∴AC⊥平面PBC…………4分
又AC 平面PAC,∴平面PAC⊥平面PBC…………5分
平面PAC,∴平面PAC⊥平面PBC…………5分
(2)解:设FE的延长线与AC的延长线交于M,连MB,
则MB为平面BEF与平面ABC的交线…………6分
在平面PCA中,由已知E是PC的中点,F是PA的四等分点,
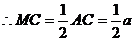 …………7分
…………7分
取BC的中点H,则EH//PB, ∴EH⊥底面ABC…………8分
过H作HO⊥MB于O,由三垂线定理,EO⊥MB
则∠EOH为平面BEF与底面ABC所成二面角的平面角…………9分
在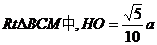 ,在
,在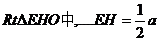 …………10分
…………10分
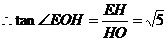 …………11分
…………11分
即平面BEF与底面ABC所成二面角的大小为 …………12分
…………12分
若利用面积射影法,指出△HDB是△EFB在底面ABC上的射影,并计算出其面积
 …………7分
计算出
…………7分
计算出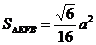 …………10分
…………10分
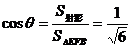 …………11分
…………11分
即平面BEF与底面ABC所成二面角的大小为 …………12分
…………12分
20.解(1)根据已知, ,
,
∴当n=1时, …………1分
…………1分
当n=2时,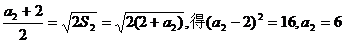 …………2分
…………2分
当n=3时,
 分别等于2,6,10…………3分
分别等于2,6,10…………3分
(2) …………4分
…………4分

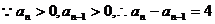 …………6分,由(1)
…………6分,由(1)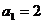 ,
,
 是以2为首项,4为公差的等差数列,
是以2为首项,4为公差的等差数列,
∴数列的通项公式 …………8分
…………8分
若用数学归纳法相应给分
(3)令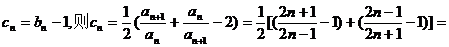
 …………10分
…………10分
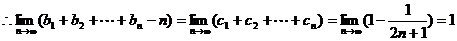 ……12分
……12分
21.解(1)∵函数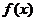 图象关于原点对称,∴对任意实数
图象关于原点对称,∴对任意实数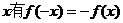 ,
,
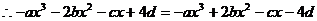 ,即
,即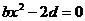 恒成立……1分
恒成立……1分
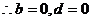 …………2分
…………2分
 ,
,
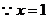 时,
时,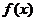 取极小值
取极小值 ,解得
,解得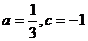 …4分
…4分
(2)当 时,图象上不存在这样的两点使结论成立.…………5分
时,图象上不存在这样的两点使结论成立.…………5分
假设图象上存在两点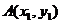 、
、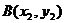 ,使得过此两点处的切线互相垂直,
,使得过此两点处的切线互相垂直,
则由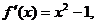 知两点处的切线斜率分别为
知两点处的切线斜率分别为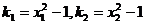 ,
,
且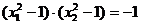 …………(*)…………7分
…………(*)…………7分
 、
、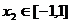 ,
,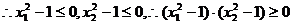
此与(*)相矛盾,故假设不成立.………………8分
证明(3) ,
,
或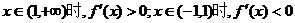 ,
,
 上是减函数,且
上是减函数,且 ……10分
……10分
∴在[-1,1]上,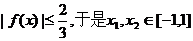 时,
时,
 .…………12分
.…………12分
22.解(1)由 …………1分
…………1分
又 ………2分
………2分
 ,故所求的轨迹方程是
,故所求的轨迹方程是 ……4分
……4分
(2)设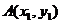 、
、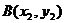 ,把
,把 ,得
,得
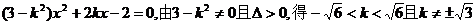 ……6分
……6分
∵A、B在y轴的同一侧, ,得到
,得到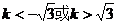 …………7分
…………7分
综上,得 .…………8分
.…………8分
(3)由(2)得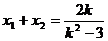 …………①
…………① 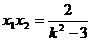 …………②
…………②
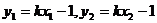 ……③………………9分
……③………………9分
∵曲线C与x轴交点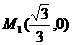 、
、 ,若存在实数k,符合题意,则
,若存在实数k,符合题意,则
 不妨取点
不妨取点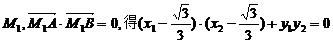 ……11分
……11分
将①②③式代入上式,整理得到 ,解得
,解得 舍去)……13分
舍去)……13分
根据曲线的对称性,知存在实数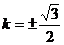 ,使得以AB为直径的圆恰好过M点…14分
,使得以AB为直径的圆恰好过M点…14分