
1.平面 、
、 互相平行的一个充分条件是 ( )
互相平行的一个充分条件是 ( )
A. 、
、 垂直于同一个平面 B.
垂直于同一个平面 B. 、
、 垂直于同一条直线
垂直于同一条直线
C. 、
、 与同一个平面所成的角相等 D.
与同一个平面所成的角相等 D. 、
、 与同一条直线所成的角相等
与同一条直线所成的角相等
2.已知直线 平行,则a= ( )
平行,则a= ( )
A.0 B.1 C.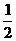 D.
D.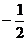
3.公差为d的等差数列{an}的前n项和为Sn,若S2=8,S3=15,则d= ( )
A.2 B.-2 C.3 D.7
4.设函数 的图象关于直线x=1对称,则f (x)=( )
的图象关于直线x=1对称,则f (x)=( )
A. B.
B.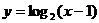
C. D.
D.
5.设2 是第二象限的角,则复数
是第二象限的角,则复数 在复平面内对应的点位于(
)
在复平面内对应的点位于(
)
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.表示振动的函数 的振幅为 ( )
的振幅为 ( )
 A.2 B.
A.2 B.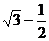 C.
C.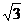 D.
D.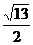
7.如图,正方体ABCD-A1B1C1D1中,点E、F分别
在棱AD、CC1上,若AF⊥A1E,则( )
A.AE=ED B.AE=C1F
C.AE=CF D.C1F=CF
8.定义在R上的函数f (x)满足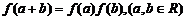 ,且
,且 ( )
( )
A.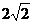 B.4 C.
B.4 C.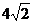 D.8
D.8
9. 如图,C为定圆A(A为圆心)上的动点,B为圆
如图,C为定圆A(A为圆心)上的动点,B为圆
A内一定点,线段BC的垂直平分线交AC于M,
则点M的轨迹是( )
A.椭圆 B.双曲线
C.抛物线 D.圆
10.从红、黄两色分别印有A、B、C、D的8张卡片中任取4张,其中字母不同且颜色齐全的概率为 ( )
A.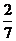 B.
B.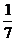 C.
C.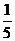 D.
D.
11.设 ( )
( )
A.0 B. C.n! D.(-1)nn!
C.n! D.(-1)nn!
12.设a1≤a2≤a3,b1≤b2≤b3为两组实数,c1,c2,c3为b1,b2,b3的任一排列,设
P=a1b1+a2b2+a3b3,Q=a1b3+a2b2+ a3b1,R=a1c1+a2c2+a3c3,则必有 ( )
A.P≤Q≤R B.R≤P≤Q C.P≤R≤Q D.Q≤R≤P
第Ⅱ卷(非选择题,共90分)
13.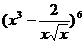 的展开式中的常数项是
.
的展开式中的常数项是
.
14.若实数 .
.
15.如果 是奇函数,则
是奇函数,则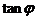 =
.
=
.
16.质点从数轴的原点出发,当投下的均匀硬币出现正面时,质点沿数轴正方向移动一个长度单位,当硬币出现反面时,质点沿数轴负方向移动一个长度单位,移动4次停止,则停止运动时质点在数轴上的坐标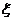 的期望是
.
的期望是
.
17.(本小题满分12分)
 如图,正三棱锥ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3.
如图,正三棱锥ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3.
(Ⅰ)求证:平面A1CB⊥平面ACB1;
(Ⅱ)求异面直线B1C与AB所成的角.
18.(本小题满分12分)
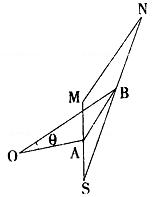
已知 对于任意点M,点M关于A点的对称点为S,点S关于B点的对称点为N.
对于任意点M,点M关于A点的对称点为S,点S关于B点的对称点为N.
(Ⅰ)用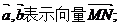
(Ⅱ)设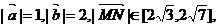 求
求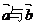 的夹角
的夹角 的取值范围.
的取值范围.
19.(本小题满分12分)
在数列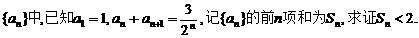
20.(本小题满分12分)
军事演习中,我方对敌设施进行炮击,假设每次炮击命中的概率为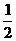 .若第一次命中,只能给该设施以重创,而不能将其摧毁,第二次命中才能将其摧毁.
.若第一次命中,只能给该设施以重创,而不能将其摧毁,第二次命中才能将其摧毁.
(Ⅰ)若对敌设施独立进行了五次炮击,试求将其摧毁的概率;
(Ⅱ)为确保将敌设施摧毁的概率达到90%以上,至少要对其独立炮击多少次?
21.(本小题满分12分)
垂直于x轴的直线交双曲线 于M、N不同两点,A1、A2分别为双曲线的左顶点和右顶点,设直线A1M与A2N交于点P(x0,y0)
于M、N不同两点,A1、A2分别为双曲线的左顶点和右顶点,设直线A1M与A2N交于点P(x0,y0)
(Ⅰ)证明: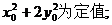
(Ⅱ)过P作斜率为 的直线l,原点到直线l的距离为d,求d的最小值.
的直线l,原点到直线l的距离为d,求d的最小值.
22.(本小题满分14分)
已知函数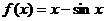
(Ⅰ)若
(Ⅱ)若
(Ⅲ)若 的大小关系(不必写出比较过程).
的大小关系(不必写出比较过程).
河北省唐山市2005-2006高三年级第二次模拟考试 数 学 试 卷(理科) 本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟. 第I卷(选择题,共60分) 参考公式: 如果事件A、B互斥,那么 P(A+B)=P(A)+P(B) 如果事件A、B相互独立,那么 P(A.B)=P(A).P(B) 如果事件A在一次试验中发生的概率是P参考答案
数学试卷(理科)参考答案
一、BCABA BCDAC DD
二、
13.240 14.6 15.-2 16.0
三、(17)(Ⅰ)证明∵四边形BCC1B1为矩形
∴BC⊥BB1,又AB⊥BC,AB∩BB1=B
∴BC⊥平面A1ABB1…………2分
又AB1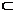 平面A1ABB1
∴BC⊥AB1
平面A1ABB1
∴BC⊥AB1
由四边形A1ABB1为菱形
∴AB1⊥A1B,又A1B∩BC=B
∴AB1⊥平面A1CB……4分
AB1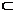 平面ACB1
∴平面A1CB⊥平面ACB1……6分
平面ACB1
∴平面A1CB⊥平面ACB1……6分
(Ⅱ)解:∵A1B1∥AB
∴A1B1与B1C所成角为异面直线B1C与AB所成的角……8分
由∠A1AB=60°,AB=4,BC=3
∴B1B=A1B=4,B1C=5,A1C=5
从而求得
∴异面直线B1C与AB所成的角为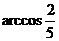 ……12分
……12分
18.解:(Ⅰ)依题意,A为MS的中点,B为NS的中点

(Ⅱ)
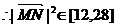
由(Ⅰ)得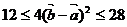

19.证明:当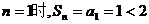 ……1分
……1分

20.解:(Ⅰ)炮击五次将敌设施摧毁,至少应击中两次,其概率为
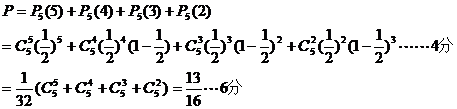
(Ⅱ)对敌设施独立炮击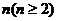 次,至少击中两次的概率为
次,至少击中两次的概率为
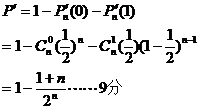

所以,至少要对敌设施独立炮击7次才能保证将其摧毁的概率超过90%……12分
21.解(Ⅰ)证明: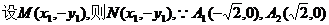
 ①
①
直线A2N的方程为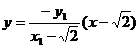 ②……4分
②……4分
①×②,得

(Ⅱ)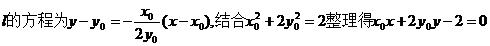
 ……10分
……10分
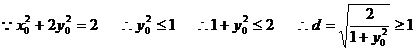
当 ……12分
……12分
22.解:(Ⅰ)

(Ⅱ)设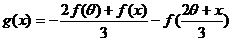
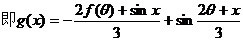
 ……6分
……6分




(Ⅲ)在题设条件下,当k为偶数时
当k为奇数时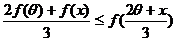 ……14分
……14分