
1.若p、q为简单命题,则“p且q为假”是“p或q为假”的
A.充分不必要的条件 B.必要不充分的条件
C.充要条件 D.既不充分也不必要的条件
2.已知复数z1=2-3i,z2= ,则
,则 等于
等于
A.1+2i B.1-2i C.-1-2i D.-1+2i
3.设{an}是正项等比数列,且a5a6=10,则lga1+lga2+…+lga9+lga10等于
A.5 B.l+lg5 C.2 D.10
4.若实数x,y满足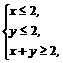 则x+2y的最小值与最大值分别是
则x+2y的最小值与最大值分别是
A.2,6 B.2,5 C.3,6 D.3,5
5.已知直线m、n与平面α、β,给出下列四个命题:
①若m∥α,n∥α,则m∥n;②若m∥α,n⊥α,则n⊥m;
③若m⊥α,m∥β,则α⊥β;④若m∥n,m∥α,则n∥α.
其中真命题的个数是
A.0 B.1 C.2 D.3
6.设函数f(x)=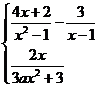
 在点x=1处连续,则a等于
在点x=1处连续,则a等于
A.-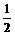 B.
B.
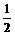 C.-
C.-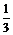 D.
D.
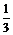
7.设函数f(x)=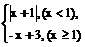 则不等式f(x)≥1的解集是
则不等式f(x)≥1的解集是
A.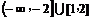 B.(-∞,-2)∪(0,2)
B.(-∞,-2)∪(0,2)
C. 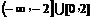 D.[-2,0]∪[2,+∞)
D.[-2,0]∪[2,+∞)
8.给出下列四个函数
f(x)=-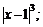 g(x)=1-||x|-1|;
g(x)=1-||x|-1|;
 φ(x)=
φ(x)= h(x)=
h(x)=
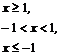 及它们的图象
及它们的图象
则图象①,②,③,④分别对应的函数为
A.φ(x),h(x),g(x),f(x) B.φ(x),g(x),h(x),f(x).
B.φ(x),h(x),f(x),g(x) D.φ(x),g(x),f(x),h(x).
9.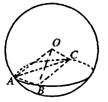 如图,A、B、C是表面积为48π的球面上三点,AB=2,BC=4,∠ABC=60°,O为球心,则直线OA与截面ABC所成的角等于
x
如图,A、B、C是表面积为48π的球面上三点,AB=2,BC=4,∠ABC=60°,O为球心,则直线OA与截面ABC所成的角等于
x
A.arcsin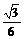 B.arccos
B.arccos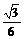
C.arcsin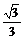 D.arccos
D.arccos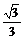
10.已知F1和F2是两个定点,椭圆C1与等轴双曲线C2都以F1、F2为焦点,点P是C1与C2的一个交点,且∠F1PF2=90°,则椭圆C1的离心率是
A. 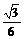 B.
B.
 C.
C.
 D.
D.

11.已知函数y=sin(ωx+φ)与直线y=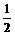 的交点中,距离最近的两点间的距离为
的交点中,距离最近的两点间的距离为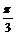 ,那么此函数的最小正周期是
,那么此函数的最小正周期是
A. 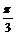 B.π C.2π D.4π
B.π C.2π D.4π
12.一个机器人每一秒钟前进一步或后退一步,程序设计师设计的程序是让机器人以先前进3步,然后再后退2步的规律移动,如果将机器人放在数轴的原点,面向正的方向在数轴上移动(1步的距离为1个单位长度).令P(n)表示第n秒时机器人所在位置的坐标,且记P(0)=0,则下列结论中错误的是
A.P(3)=3 B.P(5)=1 C. P (2007)>P(2006) D.P(2003)<P(2006)
第Ⅱ卷(非选择题 共90分)
13.在△ABC中,∠B=30°,AC= ,BC=3,则∠C的大小为___________.
,BC=3,则∠C的大小为___________.
14.为了了解商场某日旅游鞋的销售情况,抽取了
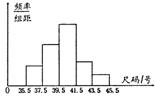 部分顾客购鞋的尺寸,将所得的数据整理后,画出
部分顾客购鞋的尺寸,将所得的数据整理后,画出
频率分布直方图如图.已知中从左至右前3个小组
的频率之比为1∶2∶3,第4小组与第5小组的
频率分别为0.175和0.075,第二小组的频数为10,则抽取的顾客人数是________.
15.如果直线l将圆x2+y2-2x-4y=0平分,且不经过第四象限,那么l的斜率的取值范围是________.
16.将一个四棱锥V-ABCD的每个顶点染上一种颜色,并使每一条棱的两端异色,若只有4种颜色可供使用,则不同的染色方法种数为__________.(用数字作答)
17.(本小题满分12分)
已知向量
(Ⅰ)求sinα-cosα的值;
(Ⅱ)求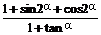 的值.
的值.
18.(本小题满分12分)
甲袋中装有2个白球1个黑球,乙袋中装有3个白球1个红球,现从甲袋中连续三次有放回地摸出一球,从乙袋中连续两次有放回地摸出一球.
(Ⅰ)求从甲袋中恰有一次摸出白球同时在乙袋中恰有一次摸出红球的概率;
(Ⅱ)求从甲袋中摸出白球的次数与从乙袋中摸出白球的次数之和为2的概率;
(Ⅲ)设从甲袋中摸出白球的次数为随机变量ζ,求Eζ.
19.(本小题满分12分)
如图所示,直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°,E为BB1的中点,点D在AB上且DE= .
.
(Ⅰ)求证:CD⊥面A1ABB1;
(Ⅱ)求二面角C-AE-D的大小;
(Ⅲ)求点A1到平面CDE的距离.
20.(本小题满分12分)
已知a<2,f(x)=(x2+ax+a)e-x
(Ⅰ)当a=1时,求f(x)的单调区间;
(Ⅱ)是否存在实数a,使f(x)的极大值为3?若存在,求出a的值,若不存在,请说明理由.
21.(本小题满分12分)
在直角坐标平面内,△ABC的两个顶点A,B的坐标分别为A(-1,0),B(1,0)平面内两点G,M同时满足以下条件:
①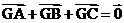 ;②
;②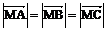 ;③
;③
(Ⅰ)求△ABC的顶点C的轨迹方程;
(Ⅱ)过点P(2,0)的直线l与△ABC的顶点C的轨迹交于E,F两点,求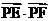 的取值范围.
的取值范围.
22.(本小题满分14分)
设数列{an}的各项都是正数,且对任意n∈N*都有a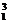 +a
+a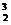 +a
+a ,其中Sn为数列{an}的前n项和.
,其中Sn为数列{an}的前n项和.
(Ⅰ)求证:a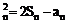 ;
;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)设bn=3n+(-1)n-1λ.2an(λ为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,都有bn+1>bn成立.
泰安市2006年高三第一轮复习质量检测
泰安市2006年高三第一轮复习质量检测数学(理) 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至9页,满分150分,考试时间120分钟. 第Ⅰ卷(选择题 共60分) 参考公式: 如果事件A、B互斥,那么 球的表面积公式 P(A+B)=P(A)+P(B) S=4πR2 如果事件A、B相互独立,那么 其中R表示球的半径 P(参考答案
数学试题参考答案及评分标准(理科)
一、选择题:本题共12个小题,每小题5分,共60分.
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
B |
B |
A |
A |
C |
D |
C |
C |
D |
A |
B |
D |
二、填空题:本题共4个小题,每小题4分,共16分.
13.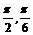 14.40 15.[0,2] 16.72
14.40 15.[0,2] 16.72
三、解答题:本题共6个小题,共74分.
17.(本小题满分12分)
解:(Ⅰ)∴ =(sinα,1)共线
t
=(sinα,1)共线
t
∴sinα+cosα=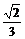 ……………………………………………………………… 2分
……………………………………………………………… 2分
故sin2α=-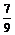
从而(sinα-cosα)2=1-sin2α=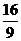 ……………………………………………… 4分 x
……………………………………………… 4分 x
∴α∈(- )∴sinα<0,cosα>0
)∴sinα<0,cosα>0
∴sinα-cosα=- …………………………………………………………………6分
…………………………………………………………………6分
(Ⅱ)∵ =2cos2α=1+cos2α……9分
=2cos2α=1+cos2α……9分
又cos2α=cos2α-sin2α=(cosα+sinα)(cosα-sinα)=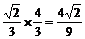
∴原式=1+ …………………………………………………………………… 12分
…………………………………………………………………… 12分
18.(本小题满分12分)
解:(Ⅰ)由题意知,从甲袋中摸出白球和从乙袋中摸出红球是相互独立的,则
P=C .
. .(
.(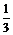 )2.C
)2.C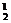 .
.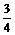 .
.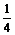 =
= ………………………………………………3分
………………………………………………3分
(Ⅱ)由题意知,事件A:从甲袋中摸出白球2次,从乙袋中摸出白球0次;事件B:从甲、乙袋中摸出白球各1次,事件C:从甲袋中摸出白球0次,从乙袋中摸出白球2次,则
P(A)=C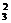 .(
.( )2.
)2.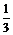 .C
.C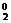 .(
.(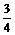 )0.(
)0.(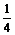 )2=
)2= ……………………………………… 5分
……………………………………… 5分
P(B)=C .
. .(
.(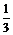 )2.C
)2.C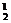 .
.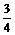 .
.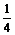 =
= …………………………………………… 7分
…………………………………………… 7分
P(C)=C .(
.( )0(
)0(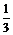 )3.C
)3.C (
(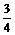 )2(
)2(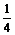 )0=
)0= …………………………………………9分
…………………………………………9分
又事件A、B、C互斥
∴所求事件的概率为:
P(A)+P(B)+P(C)=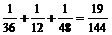 ………………………………………………10分
………………………………………………10分
(Ⅲ)由题意知,随机变量ζ服从二项分布ζ~B(3, )
)
∴Eζ=3× =2……………………………………………………………………
12分
=2……………………………………………………………………
12分
19.(本小题满分12分)
解:(Ⅰ)∵ABC-A1B1C1为直三棱柱
∴B1B⊥AB,又BE=1,DE=
∴BD=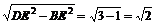
又AB=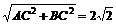 ……………………………………………………………2分
……………………………………………………………2分
∴D为AB中点,由于AC=BC
∴CD⊥AB.
由已知,面ABB1A1⊥面ABC
∴CD⊥面A1ABB1……………………………………………………………………4分
(Ⅱ)由(Ⅰ)知CD⊥面A1ABB1,过D作DF⊥AE于F,连FC,则FC⊥AE,
故∠DFC为二面角C-AE-D的平面角………………………………………… 6分
∵BE=1,AB=2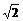 ,AE=
,AE=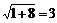
在Rt△ABE中
,sin∠DAE=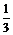
在Rt△ADF中,DF=AD.sin∠DAE=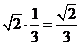
在Rt△CDF中,tan∠DFC=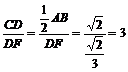
∴∠DFC=arctan3
即二面角C-AE-D大小为arctan3. …………………………………………………9分
(Ⅲ)连接A1D、A1E,∵A1B1=2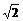 ,AA1=2,AD=
,AA1=2,AD=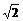 ,B1E=1
,B1E=1
∴A1E=3,A1D= ,
,
又DE= ,∴A1D⊥DE.
,∴A1D⊥DE.
又∵CD⊥平面A1ABB1,∴CD⊥A1D.
故A1D⊥平面CDE,即A1D为点A1到平面CDE的距离
∴点A1到平面CDE的距离为 .…………………………………………………
12分
.…………………………………………………
12分
20.(本小题满分12分)
解:(Ⅰ)当a=1时,f′(x)=e-x(-x2+x)
当f′(x)>0时,0<x<1
当f′(x)0<时,x>1或x<0
所以,f(x)的单调递增区间为(0,1),单调递减区间为(-∞,0),(1,+∞) ……4分
(Ⅱ)f′(x)=(2x+a)e-x-e-x(x2+ax+a)=e-x[-x2+(2-a)x]
令f′(x)=0,得x=0或x=2-a…………………………………………………………6分
列表如下:
|
x |
(-∞,0) |
0 |
(0,2-a) |
2-a |
(2-a,+∞) |
|
f′(x) |
- |
0 |
+ |
0 |
- |
|
f(x) |
↘ |
极小 |
↗ |
极大 |
↘ |
由表可知f极大(x)=f(2-a)=(4-a)ea-2…………………………………………………8分
设g(a)=(4-a)ea-2
g′(a)=-ea-2+ea-2(4-a)=(3-a).ea-2>0
∴g(a)在(-∞,2]上是增函数…………………………………………………… 10分
∴g(a)<g(2)=2<3
∴(4-a)ea-2≠3
∴不存在实数a,使得f(x)的极大值为3. ……………………………………… 12分
21.(本小题满分12分)
解:(Ⅰ)设点C,G的坐标分别为(x,y),(x0,y0),
 =(-1-x0,-y0)+(1-x0,-y0)+(x-x0,y-y0)
=(-1-x0,-y0)+(1-x0,-y0)+(x-x0,y-y0)
=(x-3x0,y-3y0)=
∴ ……………………………………………………………2分
……………………………………………………………2分
由 和
和 ∥
∥ ,知点M的坐标为(0,y0),
,知点M的坐标为(0,y0),
由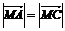 ,可得
,可得 ,
,
∴1+ ,
,
即x2+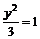 ,
,
故点C的轨迹方程是x2+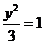 (y≠0).
………………………………………… 5分
(y≠0).
………………………………………… 5分
(Ⅱ)直线l的斜率为k(k≠0),则它的方程为y=k(x-2),
由 可得(3+k2)x2-4k2x+4k2-3=0,
可得(3+k2)x2-4k2x+4k2-3=0,
其中△=16k2-4(3+k2)(4k2-3)=36(1-k2)>0,
∴-1<k<1且k≠0……………………………………………………………………7分
设两交点E,F的坐标分别为(x1,y1),(x2,y2),由韦达定理得
x1+x2= ,x1.x2=
,x1.x2= ……………………………………………………… 8分
……………………………………………………… 8分
又因为y1=k(x1-2),y2=k(x2-2),从而
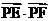 =(x1-2)(x2-2)+y1y2=(1+k2)(x1-2)(x2-2)
=(x1-2)(x2-2)+y1y2=(1+k2)(x1-2)(x2-2)
=(1+k2)( )=
)=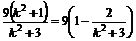 …………… 10分
…………… 10分
又0<k2<1,所以3<k2+3<4,得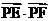 ∈(3,
∈(3,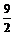 ).
).
∴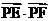 的取值范围是(3,
的取值范围是(3,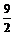 ).…………………………………………………12分
).…………………………………………………12分
22.(本小题满分14分)
解:(Ⅰ)由已知,当n=1时,a ,∵a1>0,∴a1=1.
………………………… 1分
,∵a1>0,∴a1=1.
………………………… 1分
当n≥2时, …+
…+ ①
①
 …+
…+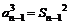 ②
②
由①-②得,a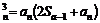 ……………………………………………………3分
……………………………………………………3分
∵an>0,
∴a =2Sn-1+an,即a
=2Sn-1+an,即a =2Sn-an,
=2Sn-an,
当n=1时,∴a1=1适合上式,
∴a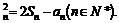 ………………………………………………………5分
………………………………………………………5分
(Ⅱ)由(Ⅰ)知,a ,即a
,即a =2Sn-an(n∈
=2Sn-an(n∈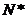 )③
)③
当n≥2时,a =2Sn-1-an-1
④
=2Sn-1-an-1
④
由③-④得,
a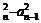 =2(Sn-Sn-1)-an+an-1=2an-an+an-1=an+an-1…………………………………… 8分
=2(Sn-Sn-1)-an+an-1=2an-an+an-1=an+an-1…………………………………… 8分
∵an+an-1>0,∴an-an-1=1,数列{an}是等差数列,首项为1,公差为1,
可得an=n. …………………………………………………………………………10分
(Ⅲ)∵an=n,∴bn=3n+(-1)n-1λ.2an=3n+(-1)n-1λ.2n, …………………………11分
要使bn+1> bn恒成立,
bn+1-bn=3n+1+(-1)nλ.2n+1-[3n+(-1)n-1λ.2n]
=2.3n-3λ(-1)n-1.2n>0恒成立
则(-1)n-1.λ<( )n-1恒成立……………………………………………………12分
)n-1恒成立……………………………………………………12分
当n为奇数时,即为λ<( )n-1恒成立
)n-1恒成立
又( )n-1的最小值为1,
)n-1的最小值为1,
∴λ<1
当n为偶数时,即为λ>-( )n-1恒成立
)n-1恒成立
又-( )n-1最大值为-
)n-1最大值为-
∴λ>- …………………………………………………………………………… 13分
…………………………………………………………………………… 13分
∴- <λ<1,又λ≠0,∴λ=-1
<λ<1,又λ≠0,∴λ=-1
∴λ=-1,使得对任意n∈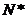 ,都有bn+1>bn……………………………………
14分
,都有bn+1>bn……………………………………
14分