
1.不等式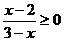 的解集是 ( )
的解集是 ( )
A.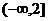 B.(3,+∞) C.(2,3) D.
B.(3,+∞) C.(2,3) D.
2.设 ,则
,则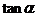 的值为 ( )
的值为 ( )
A.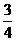 B.-
B.-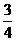 C.
C. D.-
D.-
3.设条件A:几何体的各个面都是三角形,条件B:几何体是三棱锥,则条件A是条件B的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
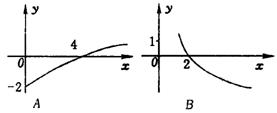
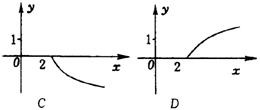 4.设
4.设 ,则函数
,则函数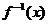 的图象为 ( )
的图象为 ( )
5.设集合M={a,b,c},N={0,1},映射f:M→N满足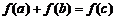 ,则映射f:M→N的个数为 ( )
,则映射f:M→N的个数为 ( )
A.1 B.2 C.3 D.4
6.设二项式 的展开式的各项系数的和为P,所有二项式系数的和为S.若有P+
的展开式的各项系数的和为P,所有二项式系数的和为S.若有P+
S=272,则n等于 ( )
A.4 B.5 C.6 D.8
7.圆心在抛物线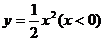 上,并且与抛物线的准线及y轴都相切的圆的方程为( )
上,并且与抛物线的准线及y轴都相切的圆的方程为( )
A.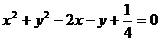 B.
B.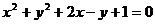
C.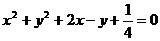 D.
D.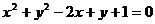
8.过△ABC的重心任作一直线分别交AB、AC于点D、E.若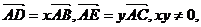 则
则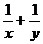 的值为 ( )
的值为 ( )
A.4 B.3 C.2 D.1
9.给出下列四个命题:
(1)各侧面在都是正方形的棱柱一定是正棱柱.
(2)若一个简单多面体的各顶点都有3条棱,则其顶点数V、面数F满足的关系式为2F-V=4.
(3)若直线l⊥平面α,l∥平面β,则α⊥β.
(4)命题“异面直线a、b不垂直,则过a的任一平面与b都不垂直”的否定.
其中,正确的命题是 ( )
A.(2)(3) B.(1)(4) C.(1)(2)(3) D.(2)(3)(4)
10.一个正方体,它的表面涂满了红色.在它的每个面上切两刀,可得27个小立方块,从中任取2个,其中恰有1个一面涂有红色,1个两面涂有红色的概率为 ( )
A.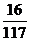 B.
B.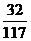 C.
C.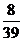 D.
D.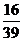
11.设三棱锥的三个侧面两两互相垂直,且侧棱长均为 ,则其外接球的表面积为(
)
,则其外接球的表面积为(
)
A.48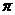 B.36
B.36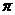 C.32
C.32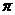 D.12
D.12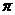
12.设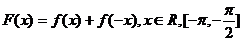 是函数F(x)的单调递增区间,将F(x)的图象按a
是函数F(x)的单调递增区间,将F(x)的图象按a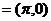 平移得到一个新的函数G(x)的图象,则G(x)的单调递减区间必定是 ( )
平移得到一个新的函数G(x)的图象,则G(x)的单调递减区间必定是 ( )
A.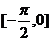 B.
B. C.
C.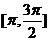 D.
D.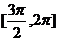
第Ⅱ卷(非选择题 共90分)
13.某单位有职工160名,其中业务人员120名,管理人员16名,后勤人员24名.为了解职工的某种情况,要从中抽取一个容量为20的样本,若用分层抽样的方法,抽取的业务人员、管理人员、后勤人员的人数应分别为 .
14.若双曲线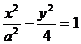 过点
过点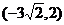 ,则该双曲线的焦距为 .
,则该双曲线的焦距为 .
15.某地区预计2004年的前x个月内对某种商品的需求总量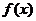 (万件)与月份
(万件)与月份 的近似关系式是
的近似关系式是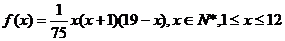 ,则2004年的第x月的需求量g(x)(万件)与月份x的函数关系式是
.
,则2004年的第x月的需求量g(x)(万件)与月份x的函数关系式是
.
16.若直线y=x是曲线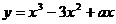 的切线,则a=
.
的切线,则a=
.
17.(本小题满分12分)
张华同学骑自行车上学途中要经过4个交叉路口,在各交叉路口遇到红灯的概率都是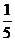 (假设各交叉路口遇到红灯的事件是相互独立的).
(假设各交叉路口遇到红灯的事件是相互独立的).
(1)求张华同学某次上学途中恰好遇到3次红灯的概率.
(2)求张华同学某次上学时,在途中首次遇到红灯前已经过2个交叉路口的概率.
18.(本小题满分12分)
已知函数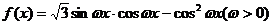 的周期为
的周期为
(1)求ω的值.
(2)设△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,求此时函数f(x)的值域.
19.(本小题满分12分)
如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD,侧面PBC⊥底面ABCD.
(1)PA与BD是否相互垂直,请证明你的结论.
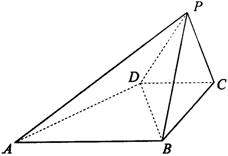 (2)求二面角P-BD-C的大小.
(2)求二面角P-BD-C的大小.
(3)求证:平面PAD⊥平面PAB.
20.(本小题满分12)
设函数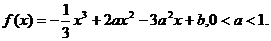
(1)求函数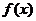 的单调区间、极值.
的单调区间、极值.
(2)若当 时,恒有
时,恒有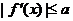 ,试确定a的取值范围.
,试确定a的取值范围.
21.(本小题满分12分)
设二次函数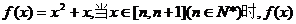 的所有整数值的个数为g(n).
的所有整数值的个数为g(n).
(1)求g(n)的表达式.
(2)设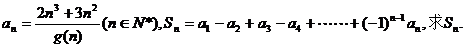
(3)设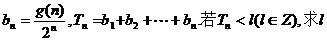 的最小值.
的最小值.
22.(本小题满分14分)
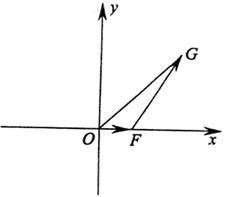
以O为原点,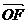 所在直线为x轴,建立如图所示的直角坐标系.设
所在直线为x轴,建立如图所示的直角坐标系.设 点F的坐标为(t,0),
点F的坐标为(t,0),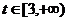 ,点G的坐标为
,点G的坐标为
(1)求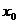 关于t的函数
关于t的函数 的表达式,判断函数
的表达式,判断函数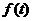 的单调性,并证明你的判断.
的单调性,并证明你的判断.
(2)设△OFG的面积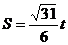 ,若以O为中心,F为焦点的椭圆经过点G,求当
,若以O为中心,F为焦点的椭圆经过点G,求当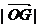 取得最小值时椭圆的方程.
取得最小值时椭圆的方程.
(3)在(2)的条件下,若点P的坐标为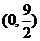 ,C、D是椭圆上的两点,且
,C、D是椭圆上的两点,且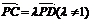 ,求实数
,求实数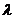 的取值范围.
的取值范围.
苏、锡、常、镇四市高三教学情况调查 数 学 第Ⅰ卷(选择题 共60分) 参考公式: 如果事件A、B互斥,那么 正棱锥、圆锥的侧面积公式 P(A+B)=P(A)+P(B) 如果事件A、B相互独立,那么 P(A.B)=P(A).P(B) 其中c表示底面周长,l表示斜高或母线长 如果事件A在一次试验中发生的概率是 球的体积公式 P,那么n次独立重复试验中恰好发生k 参考答案
数学参考答案
一、选择题
1.D 2.B 3.B 4.C 5.C 6.A 7.C 8.B 9.A 10.C 11.B 12.D
二、填空题
13.15、2、3 14.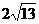 15.
15. (注:未写x的取值范围可视作正确) 16.1或
(注:未写x的取值范围可视作正确) 16.1或
三、解答题
17.(1)经过各交叉路口遇到红灯,相当于独立重复试验,所以恰好遇到3次红灯的概率为
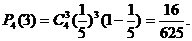 …………6分
…………6分
(2)记“经过交叉路口遇到红灯”事件A.
张华在第1、2个交叉路口末遇到红灯,在第3个交叉路口遇到红灯的概率为
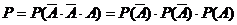 …………10分
…………10分
=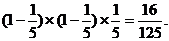 …………12分
…………12分
18.(1)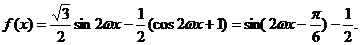 …………3分
…………3分
由函数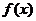 的周期
的周期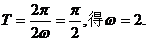 …………5分
…………5分
函数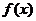 的表达式为
的表达式为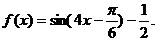 …………6分
…………6分
(2)由题意,得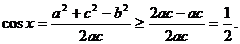 …………8分
…………8分
又 ∴
∴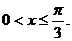 …………9分
…………9分
∴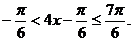 ………………10分
………………10分
∴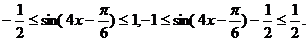
即函数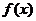 的值域为[-1,
的值域为[-1,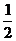 ].…………12分
].…………12分
19.解答一:
(1)PA与BD相互垂直.证明如下:
|
连结PO.…………1分 ∵PB=PC,∴PO⊥BC.
又∵平面PBC⊥平面ABCD,
平面PBC∩平面ABCD=BC,
∴PO⊥平面ABCD.…………2分
在梯形ABCD中,可得Rt△ABO≌Rt△BCD,
∴∠BEO=∠OAB+∠DBA=∠DBC+∠DBA=90°,
即AO⊥BD. ∴PA⊥BD. …………4分
(2)连结PE,由PO⊥平面ABCD,AO⊥BD,可得PE⊥BD,…………5分
∴∠PEO为二面角P-BD-C的平面角.………………6分
设AB=BC=PB=PC=2CD=2a,则在Rt△PEO中,PO=
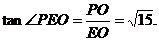 ∴二面角P-BD-C为
∴二面角P-BD-C为 …………8分
…………8分
(3)取PB的中点N,连结CN,由题意知:平面PBC⊥平面PAB,则同“(1)”可得CN⊥平面PAB. ………………9分
取PA的中点M,连结DM、MN,则由MN//AB//CD,MN=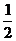 AB=CD,得四边形MNCD为平行四边形. ∴CN//DM. …………10分 ∴DM⊥平面PAB.…………11分
AB=CD,得四边形MNCD为平行四边形. ∴CN//DM. …………10分 ∴DM⊥平面PAB.…………11分
∴平面PAD⊥平面PAB.………………12分
解答二:
|
△PBC是等边三角形,
得PO⊥底面ABCD.…………1分
以BC中点O为原点,以BC所在直线为x轴,
过点O与AB平行的直线为y轴,
建立如图所示的空间直角坐标系O-xyz.……2分
设CD=1,则在直角梯形中,AB=BC=2,
在等边三角形PBC中,PO= .…………3分
.…………3分
∴A(1,-2,0),B(1,0,0)、D(-1,-1,0)、
P(0,0, ).
).
 …………4分
…………4分
(1)PA与BD相互垂直.证明如下:∵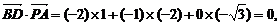
∴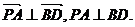 …………6分
…………6分
(2)连结AO,设AO与BD相交于点E;连结PE.
由 得
得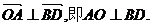
又∵AO为PA在平面ABCD内的射影,
∴PE⊥BD,∠PEO为二面角P-BD-C的平面角.…………8分
在Rt△BEO中,OE=OB.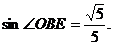
在Rt△PEO中,
∴二面角P-BD-C为 ……9分
……9分
(3)取PA的中点M,连结DM,则M的坐标为(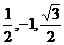 ).……10分
).……10分
又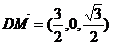 ,
,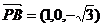 ,
,
∴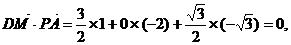
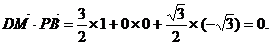
∴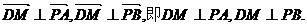 ………………11分
………………11分
∴DM⊥平面PAB. ∴平面PAD⊥平面PAB.…………12分
20.(1)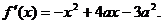 …………1分
…………1分
令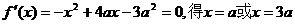 …………2分
…………2分
由表
|
x |
|
a |
|
3a |
|
||
|
f′ |
- |
0 |
+ |
0 |
- |
||
|
f |
递减 |
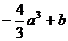 |
递增 |
b |
递减 |
可知:当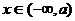 时,函数
时,函数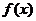 为减函数,当
为减函数,当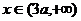 时。函数
时。函数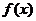 也为减函数;当
也为减函数;当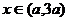 时,函数
时,函数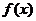 为增函数.…………5分
为增函数.…………5分
当x=a时,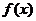 的极小值为
的极小值为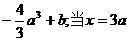 时,
时,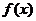 的极大值为b.……6分
的极大值为b.……6分
(2)由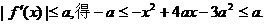 ……7分
……7分
∵0<a<1, ∴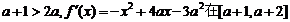 上为减函数.……8分
上为减函数.……8分
∴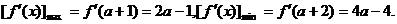 …………9分
…………9分
于是,问题转化为求不等式组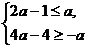 的解.…………10分
的解.…………10分
解不等式组,得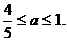 …………11分
…………11分
又0<a<1, ∴所求a的取值范围是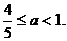 …………12分
…………12分
21.(1)当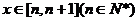 时,函数
时,函数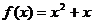 的值随x的增大而增大,则
的值随x的增大而增大,则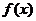 的值域为
的值域为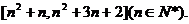 …………2分
…………2分
∴ …………3分
…………3分
(2)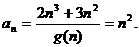 …………4分
…………4分
①当n为偶数时,

=-[3+7+……+(2n-1)]=-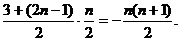 …………6分
…………6分
②当n为奇数时,

=- ………………8分
………………8分
∴
(3)由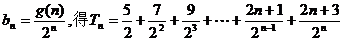 , ①
, ①
①×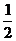 ,得
,得 ②…………9分
②…………9分
①-②,得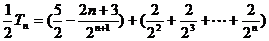
=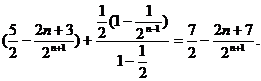
∴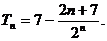 ………………11分
………………11分
则由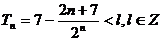 ,可得l的最小值是7.…………12分
,可得l的最小值是7.…………12分
22.(1)由题意知: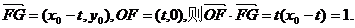 ………1分
………1分
解得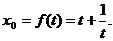 …………2分
…………2分
设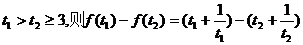
=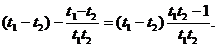
∵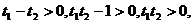 ∴
∴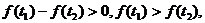
函数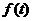 在区间[3,+∞)上单调递增.…………4分
在区间[3,+∞)上单调递增.…………4分
(2)由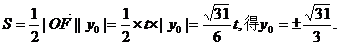 …………5分
…………5分
∴点G的坐标为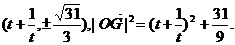 …………6分
…………6分
∵函数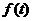 在区间[3,+∞]上单调递增,
在区间[3,+∞]上单调递增,
∴当t=3时,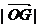 取得最小值,此时点F、G的坐标分别为
取得最小值,此时点F、G的坐标分别为
(3,0)、(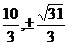 ).……7分
).……7分
由题意设椭圆方程为 …………8分
…………8分
由点G在椭圆上,得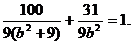 解得b2=9.
解得b2=9.
∴所求椭圆方程为 …………10分
…………10分
(3)解答一:设C、D的坐标分别为(x,y)、(m,n),
则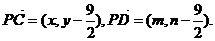
由 ………11分
………11分
∵点C、D在椭圆上,∴
消去m,得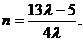 …………12分
…………12分
又∵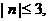 ∴
∴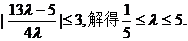 …………13分
…………13分
∴实数λ的取值范围是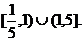 …………14分
…………14分
解答二:设点A、B的坐标分别为(0,3)、(0,-3),过点A、B分别作y轴的垂线,交直线PC于点M、N.
若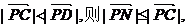 ∴1
∴1
则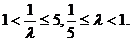 …………12分
…………12分
若 同理可得
同理可得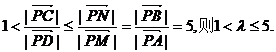 ……13分
……13分
综上,实数λ的取值范围是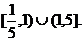 …………14分
…………14分