
1.设M和m分别表示函数y=2sinx-1的最大值和最小值,则M+m等于
A.1 B.2
C.-2 D.-1
2.设集合M={x|x2-x<0,x∈R=,N={x||x|<2,x∈R=,则M、N的关系为
A.N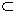 M
M
B.M∩N=M
C.M∪N=M
D.M∪N=R
3.函数y=log2(1-x)的图象是

A B C D
4.椭圆x2+my2=1的焦点在y轴上,长轴长是短轴长的两倍,则m的值为
A.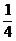 B.
B.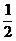 C.2
D.4
C.2
D.4
5.设Sn是等差数列{an}的前n项和,若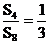 ,则
,则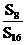 等于
等于
A. B.
B.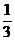 C.
C.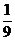 D.
D.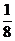
6.曲线y=x4上的点到直线x-2y-1=0的距离的最小值是
A. B.
B.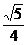 C.
C.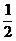 D.
D.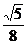
7.已知一个四面体的5条棱长都等于2,则它的体积的最大值为
A.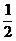 B.
B.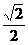 C.1
D.2
C.1
D.2
8.直线(3m+2)x-(2m-1)y+5m+1=0必过定点
A.(-1,1-) B.(1,1)
C.(1,-1) D.(-1,1)
9.如果一个三位正整数的中间一个数字比另两个数字小,如305,414,879等,则称这个三位数为凹数,那么所有凹数的个数是
A.240 B.285 C.729 D.920
10.对抛物线C:y2=4x,我们称满足y02<4x0的点M(x0,y0)在抛物线的内部,若点M(x0,y0)在抛物线内部,则直线L:y0y=2(x+x0)与曲线C
A.恰有一个公共点 B.恰有两个公共点
C.可能有一个公共点,也可能有两个公共点 D.没有公共点
11.已知|a|=3,|b|=5,且a.b=12,则a在b的方向上的投影为______.
12.某中学有高一学生400人,高二学生300人,高三学生300人,现通过分层抽样取一个样本容量为n的样本,已知每个学生被抽到的概率为0.2,则n=______.
13.在(1-x)(1+x)10的展开式中,x3的系数为______.(用数字作答)
14.设函数f(x)=lg(x2+ax-a-1),给出下列命题:①f(x)有最小值;②当a=0时,f(x)值域为R;③当a>0时,f(x)在[2,+∞)上有反函数;④若f(x)在区间[2,+∞)上单调递增,则实数a的取值范围是a≥-4,其中正确命题的序号为______.
15.(本小题满分14分)
已知向量a=(cosα,sinα),b=(cosβ,sinβ),|a-b|= .
.
(1)求cos(α-β)的值;
(2)若0<α< ,-
,- <β<0,且sinβ=-
<β<0,且sinβ=- ,求sinα的值.
,求sinα的值.
16.(本小题满分14分)
一个通讯小组有两套设备,只要其中有一套设备能正常工作,就能进行通讯.每套设备由3个部件组成,只要其中有一个部件出故障,这套设备就不能正常工作.如果在某一时间段内每个部件不出故障的概率为p,计算这一时间段内:
(1)恰有一套设备能正常工作的概率;
(2)能进行通讯的概率.
17. (本小题满分14分)
(本小题满分14分)
如图所示,在矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,PA=1.
(1)在BC边上是否存在点Q,使得PQ⊥QD,说明理由;
(2)若BC边上有且仅有一个点Q,使PQ⊥QD,求AD与平面PDQ所成角的正弦值;
(3)在(2)的条件下,能求出平面PQD与平面ABP所成的角的大小吗?
18.(本小题满分14分)
设函数f(x)=-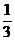 x3+2ax2-3a2x+b,0<a<1.
x3+2ax2-3a2x+b,0<a<1.
(1)求函数f(x)的单调区间、极值;
(2)若当x∈[a+1,a+2]时,恒有|f'(x)|≤a,试确定a的取值范围.
19.(本小题满分14分)
(1)已知等比例{an}的公比为q,前n项和为Sn,是否存在常数C,使数列{Sn+C}也成比数列?若存在,求出C的值;若不存在,说明理由.
(2)设等比例数列{an}的前n项和为Sn.已知S3,S9,S8成等差数列,S16-S6,S10,xS5成等比数列,求x的值.
20.(本小题满分14分)
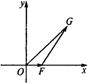 以O为原点,
以O为原点, 所在直线为x轴,建立如图所示的直角坐标系.设
所在直线为x轴,建立如图所示的直角坐标系.设 .
. =1,点F的坐标为(t,0),t∈[3,+∞),点G的坐标为(x0,y0).
=1,点F的坐标为(t,0),t∈[3,+∞),点G的坐标为(x0,y0).
(1)求x0关于t的函数x0=f(t)的表达式,判断函数f(t)的单调性,并证明你的判断;
(2)设△OFG的面积S=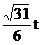 ,若以O为中心,F为焦点的椭圆经过点G,求当|
,若以O为中心,F为焦点的椭圆经过点G,求当| |取得最小值时椭圆的方程;
|取得最小值时椭圆的方程;
(3)在(2)的条件下,若点P的坐标为(0,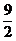 ),C、D是椭圆上的两点,且
),C、D是椭圆上的两点,且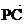 =λ
=λ (λ≠1),求实数λ的取值范围.
(λ≠1),求实数λ的取值范围.
2006浙江省普通高等学校招生统一考试模拟试卷 数 学 参考公式: 如果事件A、B互斥,那么P(A+B)=P(A)+P(B) 如果事件A、B相互独立,那么P(AB)=P(A)P(B) 如果事件A在一次试验中发生的概率是p,那么n次独立重复试验中恰好发生k次的概率Pn(k)=pk(1-p)n-k 正棱锥、圆锥的侧面积公式S锥侧=cl,其中c表示底面周长,l表示斜高或母线长 球的表面积公式S=4πR2,其中R表示球的半径 球的体积公式V=π参考答案
参考答案
一、选择题
1.C M=2-1=1,m=-2-1=-3,∴M+n=1-3=-2.
2.B M=(0,1),N=(-2,2),M∩n=(0,1)=M.
3.C 由定义域知x<1,故排除A、B,由函数单调递减,故选C.
4.A 椭圆方程为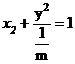 ,由题意得
,由题意得 =2×1,∴m=4.
=2×1,∴m=4.
5.A 设S4=m,则S8=3m,∴S8-S4=2m,由等差数列性质知,S12-S8=3m,S16-S12=4m,∴S16=10m,∴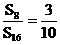 .
.
6.D 设直线L平行于直线y=2y+1,且与曲线y=x4相切于点P(x0,y0),则所求最小值d,即点P到直线y=2y+1的距离,y′=4x3=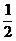 .
.
∴x0=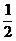 ,y0=
,y0=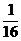 .
.
∴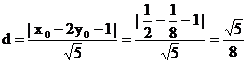 .
.
7.C 设PB=PC=AB=BC=AC=2,则当面PBC⊥面ABC时,四面体PABC体积最大,V=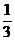 .
.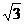 .
.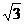 =1.
=1.
8.D 代入检验知直线过定点(-1,1).
9.B 分别将0,1,2,3……8放在十位上,则凹数个数为
 92+82+72+…+12=
92+82+72+…+12=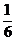 ×9×(9+1)×(2×9+1)=285.
×9×(9+1)×(2×9+1)=285.
10.D 由L与C方程消x得y2-2y0y+4x0=0(*),Δ=4y02-16x0=4(y02-4x0)<0.
∴方程(*)无实根,∴l与C无公共点.
二、填空题
11.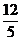 ∵a.b=|a||b|cosθ=12,|b|=5,∴|a|cosθ=
∵a.b=|a||b|cosθ=12,|b|=5,∴|a|cosθ=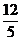 .
.
12.200
13.75 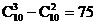 .
.
14.②③
三、解答题
15.解:(1)∵a=(cosα,sinα),b(cosβ,sinβ),
∴a-b=(cosα-cosβ,sinα-sinβ). 2分
∵|a-b|= ,
,
∴ ,
4分
,
4分
即2-2cos(α-β)= .∴cos(α-β)
.∴cos(α-β)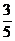 .
7分
.
7分
(2)∵0<α<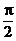 ,
,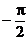 <β<0,∴0<α-β<π.
9分
<β<0,∴0<α-β<π.
9分
∵cos(α-β)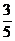 ,∴sin(α-β)=
,∴sin(α-β)= . sinβ=
. sinβ= ,∴cosβ=
,∴cosβ= . 12分
. 12分
∴sinα=sin[(α-β)+β]=sin(α-β)cosβ+cos(α-β)sinβ= .
. +
+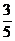 .(
.( )=
)= .
14分
.
14分
16.解:记“第一套通讯设备能正常工作”为事件A,“第二套通讯设备能正常工作”为事件B,由题意知
P(A)=p3,P(B)=p3. 2分
P( )=1-p3,P(
)=1-p3,P(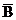 )=1-p3.
)=1-p3.
(1)恰有一套设备能正常工作的概率为P(A.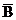 +
+ .B)=P(A.
.B)=P(A.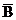 )P(
)P( .B) 4分
.B) 4分
=p3(1-p3)+(1-p3)p3=2p3-2p6. 7分
(2)解法一:两套设备都能正常工作的概率为P(A.B)=P(A).P(B)=p6. 9分
至少有一套设备能正常工作的概率,即能进行通讯的概率为P(A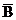 +
+ B)+P(AB)=2P3-2P6+P6=2P3-P6.
13分
B)+P(AB)=2P3-2P6+P6=2P3-P6.
13分
解法二:两套设备都不能正常工作的概率为P( .
.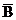 )=P(
)=P( ).P(
).P(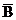 )=1(1-p3)2.
)=1(1-p3)2.
9分
至少有一套设备能正常工作的概率,即能进行通讯的概率为
1-P( .
.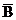 )=1-P(
)=1-P( ).P(
).P(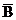 )=1(1-p3)2=2p3-p6.
13分
)=1(1-p3)2=2p3-p6.
13分
答:恰有一套设备能正常工作的概率为2p3-2p6,能进行通讯的概率为2p3-p6. 14分
17.解:(1)当BC<2时,不存在;当BC=2时,存在唯一;当BC>2时,存在两个.
4分
(2)此时,BC=2,Q为BC中点,连AQ,作AE⊥PQ于E.
∵DQ⊥PA,DQ⊥PQ,∴DQ⊥面PAQ.∴PDQ⊥面PAQ.∴AE⊥面PDQ,AE=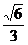 ,AD=2,sinθ=
,AD=2,sinθ= 即正弦值为
即正弦值为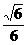 .
9分
.
9分
(3)∵PA⊥面ABCD,AB⊥DA,AB⊥BC,
BC面PBA,DA⊥面PBA,cosθ=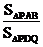 .
11分
.
11分
S△PAB=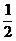 .1.1=
.1.1=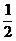 ,S△PDQ=
,S△PDQ=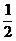 .
. .
.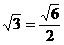 .
.
∴cosθ ,即大小为arccos
,即大小为arccos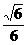 .
14分
.
14分
18.解:(1)f′(x)=-x2+4ax-3a2.
令f′(x)=-x2+4ax-3a2=0,
得x=a或x=3a. 2分
由表
|
x |
|
a |
|
3a |
|
|
y′ |
- |
0 |
+ |
0 |
- |
|
y |
递减 |
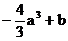 |
递增 |
b |
递减 |
可知:当x∈(-∞,a)时,函数f(x)为减函数;
当x∈(3a,+∞)时,函数f(x)也为减函数;
当x∈(a,3a)时,函数f(x)为增函数; 4分
当x=a时,f(x)的极小值为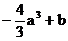 ;
;
当x=3a时,f(x)的极大值为b; 7分
(2)由|f′(x)|≤a,得-a≤-x2+4ax-3a2≤a.
∵0<a<1,
∴a+1>2a,f′(x)=-x2+4ax-3a2,在[a+1,a+2]上为减函数. 10分
∴[f′(x)]max=f′(a+1)=2a-1,
[f′(x)]min=f′(a+2)=4a-4.
于是,问题转化为求不等式组 的解.
的解.
解不等式组,得 ≤a≤1.
≤a≤1.
又0<a<1,∴所求a的取值范围是 ≤a≤1.
14分
≤a≤1.
14分
19.解:(1)①q=1时,不存在C. 2分
②Sn=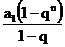 (q≠1),Sn
(q≠1),Sn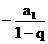 =
=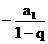 .qn.
.qn.
∴C=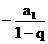 .
6分
.
6分
(2)①当q=1时,S3=3q1,S8=8q1,S9=9q1,不合题意. 8分
②当q≠1时,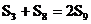 ,
,
∴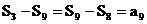 ,
,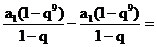
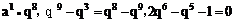 .
.
∴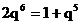 且q≠1,又
且q≠1,又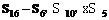 成等比数列,
成等比数列,
∴S102=xS5(S16-S6). 10分
∴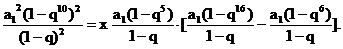
∴(1-q10)2=x(1-q5)(q6-q16).
∴1+q5=xq6,又2q6=1+q5.
∴2q6=xq6,而且q≠0.∴x=2. 14分
20.解:(1)由题意知 ,
,
 ,则
,则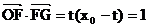 .
.
解得 .
.
设t1>t2≥3,则
∵t1-t2>0,t1t2-1>0,t1t2>0,
∴f(t1)-f(t2)>0,f(t1)>f(t2),
函数f(t)在区间[3,+∞]上单调递增. 4分
(2)由S= 得y0=
得y0= .
.
∴点Q的坐标为(t+
 ),
),
∵函数f(t)在区间[3,+∞]上单调递增,
∴当t=3时, 取得最小值,此时点F、G的坐标分别为(3,0)、(
取得最小值,此时点F、G的坐标分别为(3,0)、(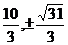 ).
).
由题意设椭圆方程为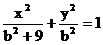 .
.
由点G在椭圆上,得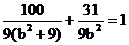 ,解得b2=9.
,解得b2=9.
∴所求椭圆方程为 .
8分
.
8分
(3)设C、D的坐标分别为(x,y)、(m,n),则 .
.
由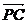 =
=
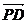 ,得
,得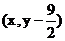 =
=
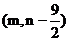 ,x=
,x= m,y=
m,y= n-
n-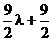 .
.
∵点C、D在椭圆上,
∴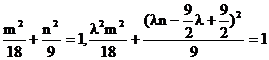 .
.
消去m,得n=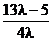 .
.
又∵|n|≤3,∴|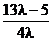 |≤3,解得
|≤3,解得 ≤
≤ ≤5.
≤5.
∴实数 的取值范围是
的取值范围是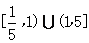 .
14分
.
14分