
1、复数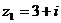 ,
,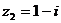 ,则
,则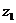 .
.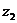 在复平面内的对应点位于( )
在复平面内的对应点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2、等差数列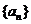 中,若
中,若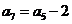 ,则
,则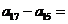 (
)
(
)
A.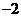 B.
B.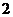 C.
C.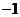 D.
D.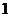
3、函数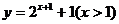 的反函数是( )
的反函数是( )
A.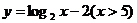 B.
B.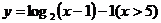
C.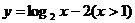 D.
D. 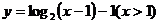
4、 条件
条件
A.充分非必要条件 B.必要非充分条件
C.既非充分也非必要条件 D.充要条件
5、一个容量为20的样本数据,分组后,组距与频数如下:
|
组距 |
(10 , 20) |
(20 , 30] |
(30 , 40] |
(40 , 50] |
(50 , 60] |
(60 , 70] |
|
频数 |
2 |
3 |
4 |
5 |
4 |
2 |
则样本在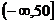 上的频率为 ( )
上的频率为 ( )
A.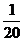 .
B.
.
B.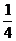 .
C.
.
C.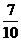 . D.
. D.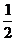
6、关于x的不等式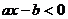 的解集为(1,+∞),则关于x的不等式
的解集为(1,+∞),则关于x的不等式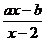 >0的解集为(
)
>0的解集为(
)
A.(-1,2) B.(-∞,-1)∪(2,+∞)
C.(1,2) D.(―∞,―2)∪(1,+∞)
7、已知函数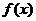 的导数为
的导数为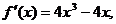 且
且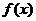 图象过点(0,-5),当函数
图象过点(0,-5),当函数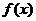 取得极小值-6时,x的值应为( )
取得极小值-6时,x的值应为( )
高三数学试卷(理) -第1页-(共8页)
A.0 B.-1 C.±1 D. 1
8、设函数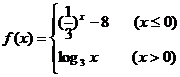 ,若f(a)>1,则实数a的取值范围是( )
,若f(a)>1,则实数a的取值范围是( )
A.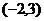 B.
B.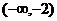 ∪
∪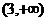 C.(3,+∞) D.
C.(3,+∞) D.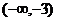 ∪(0,+∞)
∪(0,+∞)
9、已知等差数列{an}中,若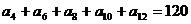 ,则
,则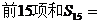 ( )
( )
A.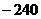 B.
B.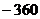 C.240 D.360
C.240 D.360
10、已知数列{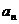 }中,
}中,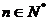 ,
,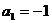 ,
,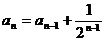 (
(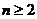 ),则
),则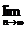
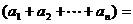 (
)
(
)
A.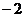 B.2 C.
B.2 C. 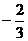 D.
D.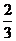
11、 已知函数f (x)的定义域为[a,b],函数f (x)的图象如右图所示,
已知函数f (x)的定义域为[a,b],函数f (x)的图象如右图所示,
则函数f (| x |)的图象是( )
A. B. C. D.
12、已知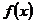 为偶函数,且
为偶函数,且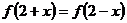 ,当
,当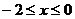 时
时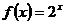 ,若
,若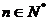 ,
,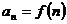 则
则 ( )
( )
A. 2006 B.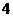 C.
C. 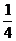 D.
D.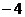
13、函数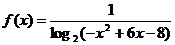 的定义域为
的定义域为
14、设函数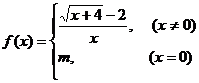 在点
在点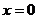 处连续,则
处连续,则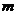 =
=
高三数学试卷(理) -第2页-(共8页)
15、过曲线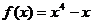 上点P处的切线平行于直线
上点P处的切线平行于直线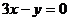 ,则点P的坐标为
,则点P的坐标为
16、某单位业务人员、管理人员、后勤服务人员人数之比依次为15∶3∶2,为了了解该单位职员的某种情况,采用分层抽样方法抽出一个容量为n的样本,
样本中业务人员人数为30,则此样本的容量n=
17、(本小题满分12分)
已知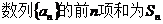 ,且
,且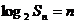 ,
,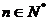 ;
;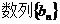 中,点
中,点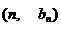 都在同一条直线上,且
都在同一条直线上,且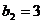 ,
,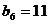 .求通项
.求通项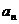 ,
,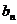
18、(本小题满分12分)
已知p: 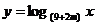 在
在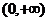 上是增函数,q:方程x2 + (m – 2 )x
+ 1 = 0有两个正根,若p和q有且只有一个正确,求实数m的取值范围.
上是增函数,q:方程x2 + (m – 2 )x
+ 1 = 0有两个正根,若p和q有且只有一个正确,求实数m的取值范围.
19、(本小题满分12分)
甲、乙两人在罚球线投球命中的概率分别为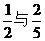 ,投中得1分,投不中得0分。甲、乙两人在罚球线各投球一次,求两人得分之和ξ的数学期望。
,投中得1分,投不中得0分。甲、乙两人在罚球线各投球一次,求两人得分之和ξ的数学期望。
20、(本小题满分12分)
已知函数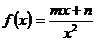 (
(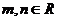 )在
)在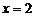 时有极值,其图象在点
时有极值,其图象在点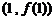 处的切线与直线
处的切线与直线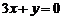 平行。
平行。
(Ⅰ)求m,n的值; (Ⅱ)求函数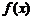 的单调区间。
的单调区间。
21、(本小题满分12分)
已知两个函数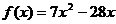 ,
, .
.
(Ⅰ)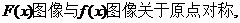 解不等式
解不等式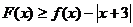
高三数学试卷(理) -第3页-(共8页)
(Ⅱ) 若对任意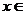 [-3,3],都有
[-3,3],都有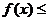
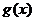 成立,求实数
成立,求实数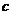 的取值范围;
的取值范围;
22、(本小题满分14分)
已知函数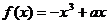 在(0,1)上是增函数.
在(0,1)上是增函数.
(1)求实数a的取值集合A;
(2)当a取A中最小值时,定义数列{an}满足: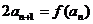 ,
,
且 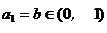 (b为常数),试证明:
(b为常数),试证明: 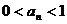
高三数学试卷(理) -第4页-(共8页)
福州市八县协作校2005―2006学年第一学期半期联考
福州市八县协作校2005―2006学年第一学期半期联考 高三年数学试卷(理科) (完卷时间:120分钟; 满分:150分) 命题人:长乐七中陈莺文 校对:谢星恩参考答案
高三年数学答案(理科)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
D |
A |
B |
B |
C |
C |
C |
B |
D |
A |
B |
C |
二、填空题:本大题共4小题,每小题4分,共16分。把答案填在答题卡的相应位置
13、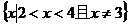 14、
14、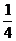 15、
15、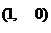 16、40
16、40
三、解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。
17、(本小题满分12分)
: 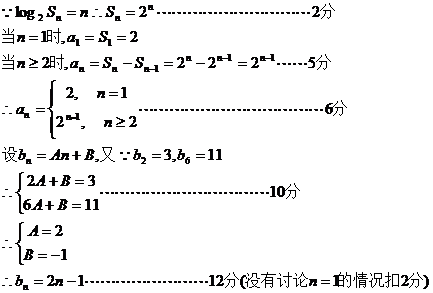
18、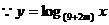 在
在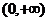 上是增函数,
上是增函数,
高三数学答案(理) -第1页-(共4页)

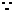 方程x2 + (m – 2
)x + 1 = 0有两个正根
方程x2 + (m – 2
)x + 1 = 0有两个正根
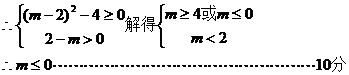
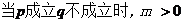
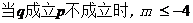
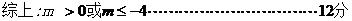
19、依题意,记“甲投一次命中”为事件A,“乙投一次命中”为事件B,则
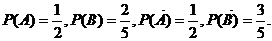
甲、乙两人得分之和ξ的可能取值为0、1、2,则ξ概率分布为:
|
ξ |
0 |
1 |
2 |
|
P |
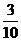 |
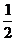 |
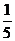 |
Eξ=0×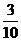 +1×
+1×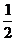 +2×
+2×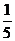 =
=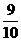
答:每人在罚球线各投球一次,两人得分之和ξ的数学期望为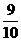 .
.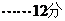 (没有“答”扣1分)
(没有“答”扣1分)
20、(Ⅰ)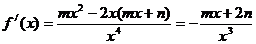
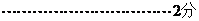
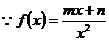 (
(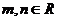 )在
)在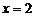 时有极值,其图象在点
时有极值,其图象在点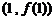 处的切线与直线
处的切线与直线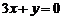 平行
平行
高三数学答案(理) -第2页-(共4页)
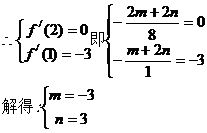
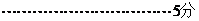
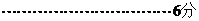
(Ⅱ)由(Ⅰ)得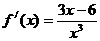
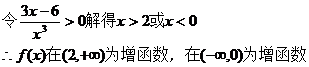

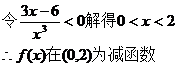
 21、(Ⅰ)设函数
21、(Ⅰ)设函数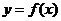 的图象上任一点
的图象上任一点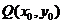 关于原点的对称点为
关于原点的对称点为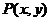 ,
,
则 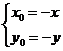 .
.
∵点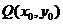 在函数
在函数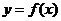 的图象上.
的图象上.
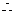
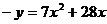 即
即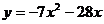 故
故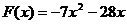
由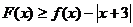 可得:
可得: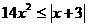
当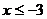 时,
时,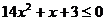
此时不等式无解。
当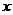
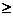
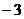 时,
时,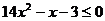

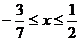
高三数学答案(理) -第3页-(共4页)
因此,原不等式的解集为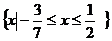 .
.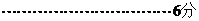
(另解: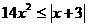 得
得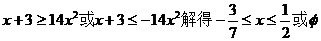

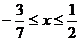 ,因此,原不等式的解集为
,因此,原不等式的解集为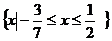 )
)
(Ⅱ)依题意: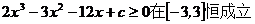
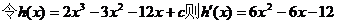
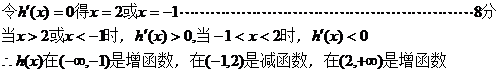
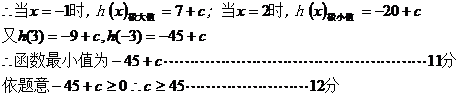
22、(1)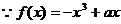 在(0,1)上是增函数
在(0,1)上是增函数
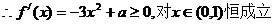
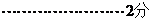
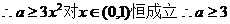
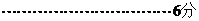
(2)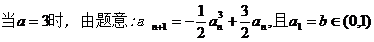
以下用数学归纳法证明: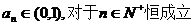
①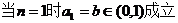
②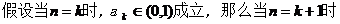
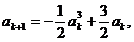 由①知
由①知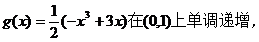
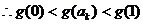 即
即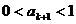
由①②知对一切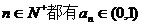
高三数学答案(理) -第4页-(共4页)