
1.设集合U={0,1,2,3,4,5},集合M={0,3,5},N={1,4,5},则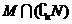
(A){5} (B){0,3} (C){0,2,3,5} (D) {0,1,3,4,5}
2.函数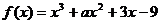 ,已知
,已知 在
在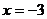 时取得极值,则
时取得极值,则 =
=
(A)4 (B)3 (C)5 (D)2
3.已知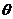 是锐角,那么下列各值中,
是锐角,那么下列各值中, 能取到的值是
能取到的值是
(A) (B)
(B)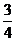 (C)
(C) (D)
(D)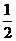
4.若命题甲的逆命题是乙,命题甲的否命题是丙,则命题乙是命题丙的
(A)逆命题 (B)逆否命题 (C)否命题 (D)否定
5.函数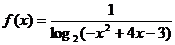 的定义域为
的定义域为
(A) (B)
(B)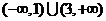 (C)(1,3) (D)[1,3]
(C)(1,3) (D)[1,3]
6.已知直线m、n,平面 ,则
,则 的一个充分不必要条件为
的一个充分不必要条件为
(A) (B)
(B)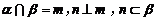
(C)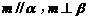 (D)
(D)
7.设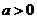 ,不等式
,不等式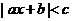 的解集是
的解集是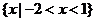 ,则
,则 等于
等于
(A) (B)
(B)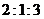 (C)
(C) (D)
(D)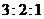
8.等差数列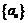 中,若
中,若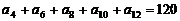 ,则
,则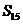 的值为:
的值为:
(A)180 (B)240 (C)360 (D)720
9.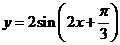 的图象是:
的图象是:
(A)关于原点成中心对称
(B)关于 轴成轴对称
轴成轴对称
(C)关于点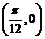 成中心对称
(D)关于直线
成中心对称
(D)关于直线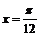 成轴对称
成轴对称
10.在R上定义运算 :x
:x y=x(1-y).若不等式(x-a)
y=x(1-y).若不等式(x-a) (x+a)<1对任意实数x成立,则
(x+a)<1对任意实数x成立,则
(A)-1<a<1 (B)0<a<2 (C) (D)
(D)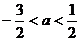
11.在重庆召开的“市长峰会”期间,某高校有14名志愿者参加接待工作.若每天排早、中、晚三班,每班4人,每人每天最多值一班,则开幕式当天不同的排班种数为
(A)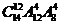 (B)
(B) (C)
(C)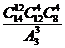 (D)
(D)
12. 定义在R上的偶函数 满足
满足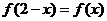 ,且在[-3,-2]上是减函数,
,且在[-3,-2]上是减函数,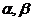 是钝角三角形的两个锐角,则下列不等式关系中正确的是
是钝角三角形的两个锐角,则下列不等式关系中正确的是
(A) (B)
(B)
(C) (D)
(D)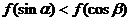
冀州中学2006届第一次诊断考试
数学(文史类) 2005.12.28
第Ⅱ卷(非选择题,共90分)
13.某校有高中生1200人,初中生900人,老师120人,现用分层抽样的方法从所有师生中抽取一个容量为 的样本;已知从初中生中抽取人数为60人,那么
的样本;已知从初中生中抽取人数为60人,那么 =_________。
=_________。
14.函数 的图象F按向量a
的图象F按向量a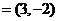 平移到G,则图象G的函数解析式为
。
平移到G,则图象G的函数解析式为
。
15.在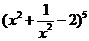 的展开式中,常数项是
。
的展开式中,常数项是
。
16.已知函数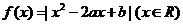 .给出下列命题:①
.给出下列命题:① 必是偶函数;②当
必是偶函数;②当
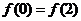 时,
时, 的图像必关于直线x=1对称;③若
的图像必关于直线x=1对称;③若 ,则
,则 在区间
在区间 上是增函数;④
上是增函数;④ 有最大值
有最大值 . 其中正确的序号是___ ____。
. 其中正确的序号是___ ____。
17.(本题满分12分)
已知sin2 .
.
(1)求cos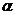 的值;
的值;
(2)求满足sin (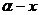 ) – sin (
) – sin (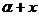 ) + 2cos
) + 2cos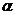 =
=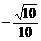 的锐角x.
的锐角x.
18.(本题满分12分)
在教室内有10个学生,分别佩带着从1号到10号的校徽,任意取3人记录其校徽的号码。
(1)求最小号码为5的概率。
(2)求3个号码中至多有一个是偶数的概率。
(3)求3个号码之和不超过9的概率。
19.(本题满分12分)
已知数列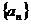 的前n项和为
的前n项和为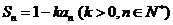
(1)用k、n表示 ;
;
(2)数列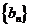 对于任意正整数n都有
对于任意正整数n都有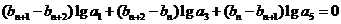 ,
,
求证:数列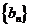 为等差数列;
为等差数列;
20.(本题满分12分)
已知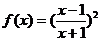
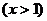 ,
,
(1)若 ,求
,求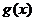 的最小值;
的最小值;
(2)若不等式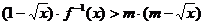 对于一切
对于一切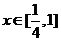 恒成立,求实数
恒成立,求实数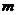 的取值范围。
的取值范围。
21.(本题满分12分)
“十一”国庆黄金周小明准备组织本班部分同学一同去旅游,费用均摊。现有甲乙两家旅行社对学生团体旅游提出如下优惠方案。甲旅行社提出:每人享受八二折(即原价的82%)优惠,如果人数多于5人,则组织者一人可全部免费,但不得分成多个旅游团,即只能组一个团。乙旅行社提出:不论人数多少,一律七五折优惠。
(1) 如果9人的一个旅游团参加甲旅行社,则人均费用优惠了多少?(精确到0.1%)
(2) 如果两家旅行社到某地的各项服务均相同,原价也相同,问选择哪家旅行社价格更优惠?
22.(本题满分14分)
已知二次函数
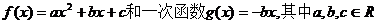 且满足
且满足
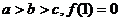 .
.
(1)证明:函数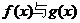 的图象交于不同的两点A,B;
的图象交于不同的两点A,B;
(2)若函数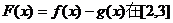 上的最小值为9,最大值为21,试求
上的最小值为9,最大值为21,试求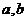 的值;
的值;
(3)求线段AB在 轴上的射影A1B1的长的取值范围.
轴上的射影A1B1的长的取值范围.
冀州中学2006届第一次诊断考试 数学(文史类) 2005.12.28 本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至8页,共150分,考试时间120分钟。 第Ⅰ卷(选择题,共60分) 1.答第Ⅰ卷前,请务必将自己的姓名、准考证号、考试科目,用铅笔涂写在答题卡上。 2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在考题卷上。 3.考试结束后,将本试卷和答题卡一并交回。 参考答案
冀州中学2006届第一次诊断考试数学(文)参考答案
2005.12.28
一、选择题:BCABAC BCDC BD
1.解:∵U={0,1,2,3,4,5} ,M={0,3,5},N={1,4,5};
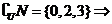
 故选B
故选B
2.解:
由已知 时,
时, 故选C
故选C
3.解:利用排除法。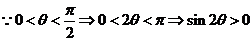 ,而B、D的
,而B、D的 ;
;
C的 ,不符合有界性。
故选A
,不符合有界性。
故选A
4.解:若甲: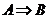 ;则乙
;则乙 ;则丙:
;则丙: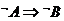 ;故乙是丙的逆否命题。故选B
;故乙是丙的逆否命题。故选B
5.解: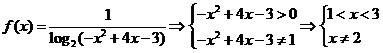 故选A
故选A
6.解:当“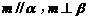 ”为条件时可推出结论“
”为条件时可推出结论“ ”成立;
”成立;
当“ ”成立时,m与
”成立时,m与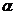 、m与
、m与 的位置关系不确定。
故选C
的位置关系不确定。
故选C
7.解: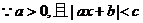 的解是:
的解是:
 ,
,
则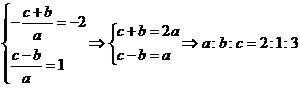 故选B
故选B
8.解:因为数列{ }为等差数列,设公差为d.
}为等差数列,设公差为d.
若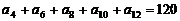 ,又因为:
,又因为:
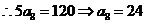
而 故选C
故选C
9.解:因为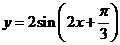
若是关于中心对称:则 ,故
,故 ,所以不关于指定的点成中心对称;
,所以不关于指定的点成中心对称;
若是关于轴对称:则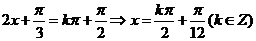
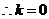 时,对称轴为
时,对称轴为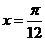 故选D
故选D
10.解:因定义运算 :x
:x y=x(1-y) ,所以不等式(x-a)
y=x(1-y) ,所以不等式(x-a) (x+a)<1
(x+a)<1
即 
又因为对一切x都成立,所以 ,即
,即
故选C
11.解:有14名志愿者,但每天早、中、晚三班,每班4人,只需12人,所以应先从14人中选出12人,然后这12人再来分组排班。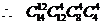 故选B
故选B
12.解: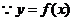 是偶函数,且在
是偶函数,且在 上是减函数,所以在
上是减函数,所以在 上是增函数;
上是增函数;
又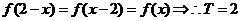
故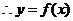 在
在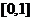 上是增函数;
上是增函数;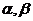 是钝角三角形的两个锐角,
是钝角三角形的两个锐角,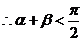
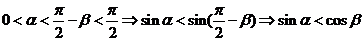 ,
,
而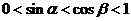
所以: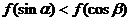 故选D
故选D
二、填空题
13.148。
解: 。
。
14.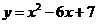
解: 
15.-252
解: 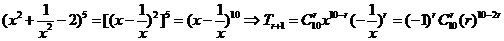
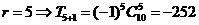
16.③
解:①不恒为偶函数;
②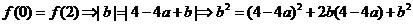 ,
,
所以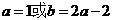 ,若
,若 关于
关于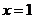 对称,
对称,
若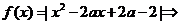 不恒关于
不恒关于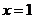 对称;
对称;
③ 时,整个图象在x轴的上方(或顶点在x轴上)
时,整个图象在x轴的上方(或顶点在x轴上)
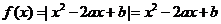 ,故
,故 在区间
在区间 上是增函数;
上是增函数;
④无最大值。(开口向上)
三、解答题
17.解:(1)因为 <
< <
<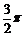 , 所以
, 所以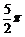 <2
<2 <3
<3 ………2分
………2分
所以cos2 = –
= –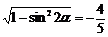 ,
………………4分
,
………………4分
由cos2 = 2 cos
= 2 cos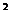
 –
1, 所以cos
–
1, 所以cos = –
= –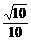 …………………… 6分
…………………… 6分
(2)因为sin
( – x) – sin(
– x) – sin( + x) + 2cos
+ x) + 2cos =-
=-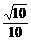
所以2cos (1– sinx) = –
(1– sinx) = –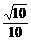 ,
……………………………10分
,
……………………………10分
所以 sin x =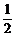 ,因为x为锐角,所以x =
,因为x为锐角,所以x = 。 ……12分
。 ……12分
18.解:(1)从10人中任取3人,共有 种,最小号码为5,相当于从6,7,8,9,10共五个中任取2个,则共有
种,最小号码为5,相当于从6,7,8,9,10共五个中任取2个,则共有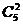 种结果。
种结果。
则最小号码为5的概率为P= 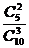 =
=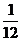 ………………(4分)
………………(4分)
(2)选出3个号码中至多有一个是偶数,包括没有偶数和恰有一个偶数两种情况,共有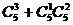 种.所以满足条件的概率为P=
种.所以满足条件的概率为P= ……(8分)
……(8分)
(3)3个号码之和不超过9的可能结果有:
(1,2,3)、(1,2,4)、(1,2,5)、(1,2,6)、(1,3,4)、(1,3,5)、(2,3,4)
则所求概率为.
P= 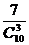 =
= ………………(12分)
………………(12分)
19.解:(1)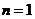 时,
时,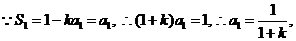
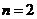 时,
时,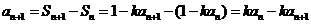 …………3分
…………3分
 数列
数列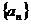 为等比数列, ………………4分
为等比数列, ………………4分
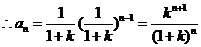 ,……………………………………………………5分
,……………………………………………………5分
(2)由题意知:

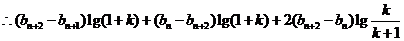
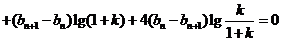 ………………8分
………………8分
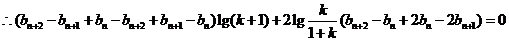
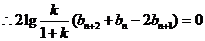 ;
;
即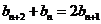 , 故数列
, 故数列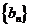 为等差数列。
……………………12分
为等差数列。
……………………12分
20.解:(1)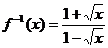
 ,
……………3分
,
……………3分
∴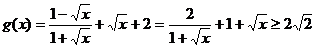 ,等号当且仅当
,等号当且仅当 ,即
,即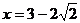 时取得。∴
时取得。∴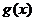 的最小值为
的最小值为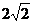 。
……………6分
。
……………6分
(2)不等式即为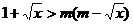 ,也就是
,也就是 ,………8分
,………8分
令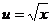 ,则
,则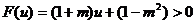 在
在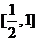 上恒成立,∴
上恒成立,∴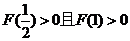 ,
解得:
,
解得: 。
……………12分
。
……………12分
21.解:旅行社给出的原价为每人a元。
(1) 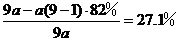 ,即优惠了27.1% ……………5分
,即优惠了27.1% ……………5分
(2) 设学生人数为n,f(n)为选择甲旅行社的费用,g(n)为选择乙旅行社的费用,根据题意得:n£5时,显然f(n)>g(n); ……………8分
当 时,f(n)=a(n-1)82%,g(n)=an×75%,由f(n)>g(n),得n³12,
时,f(n)=a(n-1)82%,g(n)=an×75%,由f(n)>g(n),得n³12,
所以,若人数为6到11人时,选择甲旅行社合算,其余情况选择乙旅行社合算。 …12分
22.(1)由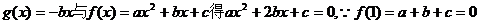 ,
,
 即函数
即函数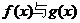 的图象交于不同的两点A,B; ……3分(2)
的图象交于不同的两点A,B; ……3分(2)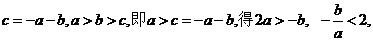
已知函数 的对称轴为
的对称轴为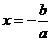 ,
,
故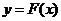 在[2,3]上为增函数,
……………6分
在[2,3]上为增函数,
……………6分
 ……8分
……8分
(3)设方程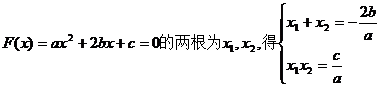
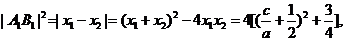 ……9分
……9分
 ……10分
……10分
设 的对称轴为
的对称轴为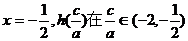 上是减函数,
上是减函数,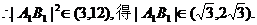 ……12分
……12分