
1、计算: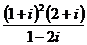 的值为
的值为
(A)-2 (B) 2 (C)2i (D)-2i
2、设集合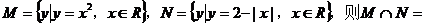
(A){(1,-1) , (-1,-1) } (B){1,-1} (C) {y | 0£ y £ 2 } (D){ y | y ³ 0 }
3、若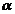 是锐角,且
是锐角,且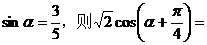

4、在等差数列{an}中,Sn是前n项的和a4=9,a9=-6,则
(A)S6=S8 (B) S7=S8 (C) S6=S7 (D)S5=S7
5、函数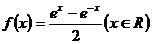 的反函数是f -1(x),则f -1(2)的值为
的反函数是f -1(x),则f -1(2)的值为

6、函数y=Asin(ωx+φ) + b的图像如图所示,则y=f(x)的解析式为
(A)y=sin2x-2
 (B) y=1-sin(2x+
(B) y=1-sin(2x+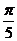 )
)
(C) y=1+sin(2x+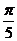 )
)
(D) y=1-sin(2x
-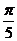 )
)
7、已知O为坐标原点,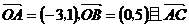 ∥
∥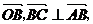 则点C的坐标为
则点C的坐标为
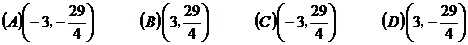
8、当x>1时,不等式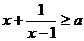 恒成立,则实数a的取值范围是
恒成立,则实数a的取值范围是
(A)(-∞,2](B)[2,+∞) (C)[3,+∞) (D) (-∞,3]
9、设是f(x)一个关于x的三次函数,且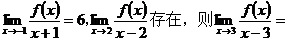

10、节日期间,某种鲜花进货价是每束2.5元,销售价是每束5元;节后卖不出的鲜花以每束1.6元的价格处理。根据前5年的销售情况预测,节日期间这种鲜花的需求量服从下表所示的分布,若进这种鲜花500束,则期望利润是
|
ξ |
200 |
300 |
400 |
500 |
|
P |
0.20 |
0.35 |
0.30 |
0.15 |
(A) 706元 (B) 690元 (C) 754元 (D)720元
11、已知函数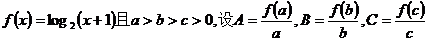 ,则
,则
(A) A>B>C (B) A>C>B (C) C>B>A (D)B>A>C
12、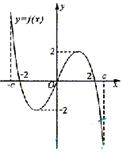 f(x)是定义在区间[-c,c]的奇函数,其图像如图所示。令g(x)=af(x)+b,则下列关于函数g(x)的叙述正确的是
f(x)是定义在区间[-c,c]的奇函数,其图像如图所示。令g(x)=af(x)+b,则下列关于函数g(x)的叙述正确的是
(A)若a<0,则函数g(x) 的图像关于原点对称
(B) 若a=-1,-2<b<0,则方程g(x)=0有大余2的实根
(C) 若a¹0,b=2,则方程g(x)=0有两个实根
(D) 若a³1, b<2,则方程g(x)=0有三个实根
乐山市高中2006届第一次诊断考试
数 学(理工农医类) 2006.1
第Ⅱ卷(非选择题,共90分)
13、若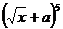 的展开式中的第四项是10a2(a为大于0的常数),则x=
;
的展开式中的第四项是10a2(a为大于0的常数),则x=
;
14、定义R在上的函数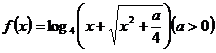 为奇函数,则
为奇函数,则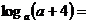
15、 如图,函数y=f(x)的图像在点P处的切线方程是
如图,函数y=f(x)的图像在点P处的切线方程是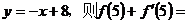
16、 如图,一单位正方体形积木,平放与桌面上,在其上放置若干个小正方体形积木摆成塔形,其中上面正方体中下底的四个顶点是下面相邻正方体中上底面各边的中点,如果所有正方体暴露在外面部分的面积和超过8.8,则正方体的个数是
.
如图,一单位正方体形积木,平放与桌面上,在其上放置若干个小正方体形积木摆成塔形,其中上面正方体中下底的四个顶点是下面相邻正方体中上底面各边的中点,如果所有正方体暴露在外面部分的面积和超过8.8,则正方体的个数是
.
17、(本题满分12分)
在△ABC中,角A、B、C的对边分别为a、b、c,且a+c=10,C=2A,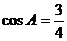 。
。
求:(1)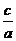 的值;(2)b的值。
的值;(2)b的值。
18、(本题满分12分)
已知a = (cos2x,sin2x),
b = (cosx,-sinx), c = (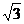 ,-1),其中
,-1),其中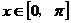 ;
;
(1)当a∥b时,求x的值的集合;
(2)设f(x) = |a - c|2,求f(x)的单调递增区间。
19、(本题满分12分)
已知等差数列{an}的首项 a1=1,公差d>0,且第二项,第五项,第十四项分别是等比数列{bn}的第二项、第三项、第四项.
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)设数列{cn}对任意的n∈N*,均有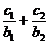 +…+
+…+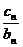 =an+1成立,
=an+1成立,
求c1+c2+…+c2006 的值.
20、(本题满分12分)
(1)已知a,b是正常数,且a ¹ b, x、y Î(0,+¥),求证: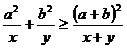 ,指出等号成立的条件;
,指出等号成立的条件;
(2)利用(1)的结论,求函数 的最小值,并指出f(x)取最小值时x的值。
的最小值,并指出f(x)取最小值时x的值。
21、(本题满分12分)
甲、乙两人掷硬币,甲用一枚硬币掷3次,记下国徽面朝上的次数为m;乙用一枚硬币掷2次,记下国徽面朝上的次数为n
(1)计算国徽面朝上不同次数的概率并填入下表:
|
国徽面朝上次数m |
3 |
2 |
1 |
0 |
||
|
P(m) |
|
|
|
|
||
|
国徽面朝上次数n |
2 |
1 |
0 |
|||
|
P(n) |
|
|
|
|||
(2)现规定:若m > n,则甲胜;若n ³ m,则乙胜。你认为这种规定合理吗?,为什么?
22、(本题满分14分)
已知函数f (x) = ln (2-x) + ax在(0,1)上是增函数;
(Ⅰ)求实数a的取值范围;
(Ⅱ)若数列{an}满足:a1 Î(0,1),an+1 = ln(2-an)+an(nÎN*),
证明:0< an < an+1 <1;
(Ⅲ)若数列{bn}满足:b1 Î(0,1),bn+1 = 2ln(2-bn)+bn(nÎN*),问数列{bn}是否具有单调性?若有单调性,请给出证明,若不存在单调性,请说明理由。
乐山市高中2006届第一次调查研究考试 数 学(理工农医类) 本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至8页,共150分,考试时间120分钟。 第Ⅰ卷(选择题,共60分) 1.答第Ⅰ卷前,请务必将自己的姓名、准考证号、考试科目,用铅笔涂写在答题卡上。 2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在考题卷上。 3.考试结束后,将本试卷和答题卡一并交回。 4.参考公式:参考答案
乐山市高中2006届第一次诊断考试数学(理)参考答案
2006.1
一、选择题:ACDCDD CDAACB
二、填空题:13、a -1 14、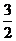 15、2 16、6
15、2 16、6
三、解答题
17、解:(1)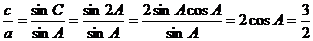
(2)由a+c=10,及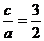 得到a=4,c=6
得到a=4,c=6
又因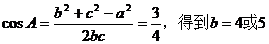
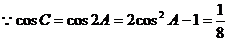
当b=4时,此时C>90°不合题意,舍去
\ b=5
18、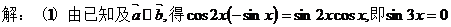
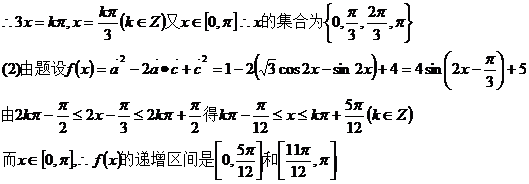
19、解:(Ⅰ)由题意,有 (a1+d)(a1+13d)=(a1+4d)2.
而a1=1, d>0,∴d=2.
∴an=2n-1.
公比q=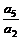 =3,a2=b2=3.
=3,a2=b2=3.
∴bn=b2.qn-2=3.3n-2= 3n-1.
(Ⅱ)当n=1时,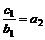 ,∴c1=1×3=3.
,∴c1=1×3=3.
当n≥2时,
∵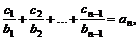 ……①
……①
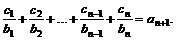 ……②
……②
②-①,得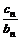 =an+1-an=2,
=an+1-an=2,
∴cn=2bn=2.3n-1(n≥2).
即有cn=
∴c1+ c2+ c3+…+ c2006=3+2(31+32+33+…+32005)
=3+2.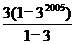 =32006.
=32006.
20、解:(1)应用二元均值不等式,得
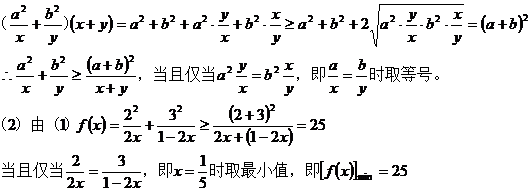
21、解:(1)
|
国徽面朝上次数m |
3 |
2 |
1 |
0 |
||
|
P(m) |
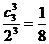 |
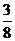 |
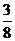 |
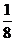 |
||
|
国徽面朝上次数n |
2 |
1 |
0 |
|||
|
P(n) |
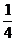 |
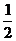 |
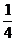 |
|||
(2)这种规定是合理的。因为甲胜,则m > n,当m=3时,n=2,1,0
其概率为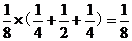
当m=2时,n=1,0,其概率为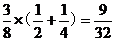
当m=1时,n=0,其概率为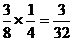 ,\甲获胜的概率为
,\甲获胜的概率为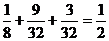
乙获胜,则m £ n,当n=2时,m=2,1,0,其概率为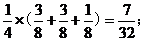
当n=1时,m=1,0,其概率为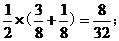
当n=0时,m=0,其概率为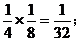
\乙获胜的概率为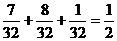
22、(Ⅰ)解:

即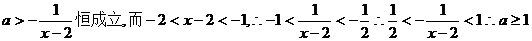
(Ⅱ)证明:由题设知,a1 Î(0,1),令0<ak<1,当n=k+1时,ak+1 = ln(2-ak)+ak>0
ak+1 = ln(2-ak)+ak<1,(由第一问知函数f (x) = ln (2-x) + x在(0,1)上是增函数)
所以0< an <1, nÎN* 又因为an+1 – an = ln(2 - an) > 0所以0< an < an+1 <1
(Ⅲ)数列{bn}不具有单调性.令g (x) = 2ln(2-x)+x
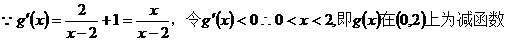
∵b1 Î(0,1),b2 = 2ln(2-b1)+b1\2ln1+1<b2<2ln2+0 ∴1< b2 < 2ln2 < 2
b3= 2ln(2-b2)+b2 ,∴b3<2ln1+1 =1 即有: b1 < b2 , b2 > b3
∴数列{bn}不具有单调性