
1. 函数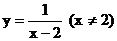 的反函数是
( )
的反函数是
( )
A. 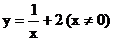 B.
B.
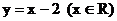
C. 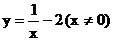 D.
D. 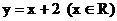
2. 直线l1, l2互相平行的一个充分条件是 ( )
A. l1, l2 都平行于同一个平面 B. l1, l2与同一个平面所成的角相等
C. l1平行于 l2 所在的平面 D. l1, l2都垂直于同一个平面
3. 若点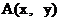 是300°角终边上异于原点的一点, 则
是300°角终边上异于原点的一点, 则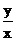 的值为 (
)
的值为 (
)
A.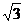 B. -
B. -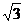 C.
C. 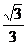 D.
-
D.
-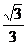
4. 函数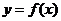 与
与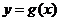 有相同的定义域,且都不是常数函数,对定义域中的任何
有相同的定义域,且都不是常数函数,对定义域中的任何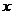 ,有
,有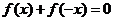 ,
,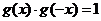 ,且当
,且当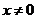 时,
时,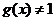 ,则
,则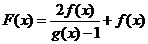 ( )
( )
A 是奇函数但不是偶函数 B 是偶函数但不是奇函数
C 既是奇函数又是偶函数 D 既不是奇函数也不是偶函数
5. 与直线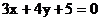 的方向向量共线的一个单位向量是
( )
的方向向量共线的一个单位向量是
( )
A. 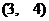 B.
B.
 C.
C.
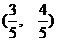 D.
D.
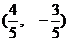
6. 已知函数f
(x)=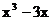 , 则函数f (x)在区间
, 则函数f (x)在区间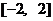 上的最大值是 ( )
上的最大值是 ( )
A. 0 B. 1 C. 2 D. 3
7. 在等比数列 中, 前n项和为S n. 若
中, 前n项和为S n. 若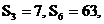 则公比q的值是
( )
则公比q的值是
( )
A. 2 B. -2 C. 3 D. -3
8. 若 为圆
为圆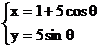
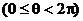 的弦的中点,则该弦所在直线的方程是( )
的弦的中点,则该弦所在直线的方程是( )
A. 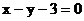 B.
B.
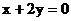 C.
C. 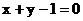 D.
D.
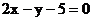
9. 已知双曲线的中心在坐标原点,离心率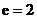 ,且它的一个顶点与抛物线
,且它的一个顶点与抛物线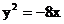 的焦点重合,则此双曲线的方程为
( )
的焦点重合,则此双曲线的方程为
( )
A. 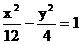 B.
B.
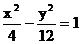 C.
C.  D.
D.
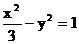
10. 已知F1和F2是两个定点,点P是以F1和F2为公共焦点的椭圆和双曲线的一个交点,并且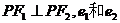 分别是椭圆和双曲线的离心率,则有 ( )
分别是椭圆和双曲线的离心率,则有 ( )
A 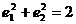 B
B
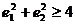 C
C
 D
D
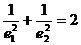
11. 设正数x
, y满足 则
则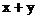 的取值范围是(
)
的取值范围是(
)
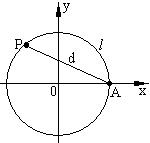 A.
A.  B.
B.
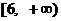
C. 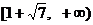 D.
D. 
12. 如图, 设点A是单位圆上的一定点, 动点P从点A出
发在圆上按逆时针方向旋转一周, 点P所旋转过的弧
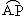 的长为l, 弦AP的长为d, 则函数
的长为l, 弦AP的长为d, 则函数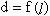 的图象
的图象
大致是 ( )

13. 函数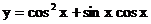 的最小正周期是
.
的最小正周期是
.
14. 如图, 在直三棱柱ABC-A1B1C1中, ∠ABC=90°,
AB=BC=AA1=2, 点D是A1C1的中点, 则异面
直线AD和BC1所成角的大小为 .
15. 函数 的定义域是
的定义域是
.
16. 已知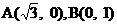 坐标原点O在直线AB上的射影为
坐标原点O在直线AB上的射影为
点C, 则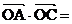 .
.
高三数学期末综合练习(四)
班级 姓名 学号 得分
13. ; 14. ;
15. ; 16. ;
的文字说明、推理过程或计算步骤)。
17. (本小题满分12分)已知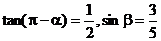 ,
, 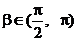 . 求
. 求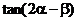 的值.
的值.
18. (本小题满分12分) 为了加快教学手段的现代化,某校计划购置一批电脑。已知甲公司的报价为每台5800元,优惠条件是购买10台以上则从第11台起可按报价的70% 计算;乙公司的报价也是每台5800元,优惠条件是每台按报价的85% 计算。假如你是学校的有关负责人,在电脑品牌、质量、售后服务等完全相同的前提下,你将选择购买哪个公司的电脑?
19. (本小题满分12分)如图, 在矩形ABCD中, AB=2BC, P, Q分别为线段AB, CD的中点, EP⊥平面ABCD.
(1) 求证: AQ∥平面CEP;
(2) 求证:平面AEQ⊥平面DEP;
(3) 若EP=AP, 求二面角Q-AE-P的大小.

20. (本小题满分12分)已知数列 的前n项和为
的前n项和为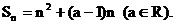 设集合
设集合
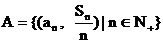 ,
,
(1) 求数列 的通项公式;
的通项公式;
(2) 若以集合A中的元素作为点的坐标,则这些点是否都在同一条直线上? 并说明理由;
(3) “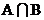 至多只有一个元素”是否正确?
如果正确, 请给予证明; 如果不正确, 请举例说明.
至多只有一个元素”是否正确?
如果正确, 请给予证明; 如果不正确, 请举例说明.
21. (本小题满分12分) 已知函数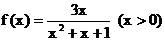 .
.
(1) 试确定函数 的单调区间,并证明你的结论;
的单调区间,并证明你的结论;
(2) 若 ≥1,
≥1, 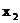 ≥1, 证明:
≥1, 证明: 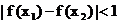
22. (本小题满分14分)已知点P与定点F 的距离和它到定直线l:
的距离和它到定直线l: 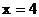 的距离之比是1 : 2.
的距离之比是1 : 2.
(1) 求点P的轨迹C方程;
(2) 过点F的直线交曲线C于A, B两点, A, B在l上的射影分别为M, N.
求证AN与BM的公共点在x轴上.
高三数学期末综合练习(四)参考答案
高三数学期末综合练习(四)
参考答案及评分标准
一. 选择题(每小题5分,共60分)
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
A |
D |
B |
C |
D |
C |
A |
A |
B |
D |
B |
C |
二. 填空题(每小题4分,共16分)
13. π ; 14. 30° ; 15.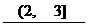 ; 16.
; 16. 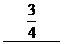 ;
;
三. 解答题(共74分)
17.(本小题满分12分)
解: 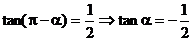 …………(2分)
…………(2分)
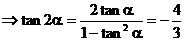 …………(4分)
…………(4分)
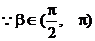 ,
,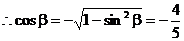 ,
,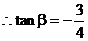 …………(8分)
…………(8分)
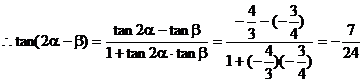 …………(12分)
…………(12分)
18.(本小题满分12分)
解: 解:设学校计划购置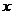 台电脑,若向甲公司购买,则总价格
台电脑,若向甲公司购买,则总价格
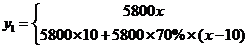
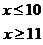 ;----------------------3分
;----------------------3分
若向乙公司购买,则总价格
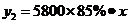 =
=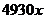 ----------------------5分
----------------------5分
⑴
当 时,显然
时,显然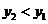 ,故应选择乙公司;
----------------------7分
,故应选择乙公司;
----------------------7分
⑵
当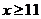 时,令
时,令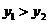 ,即:
,即: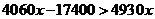
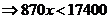
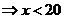 ------------------9分
------------------9分
所以:当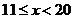 时,选择乙公司,
时,选择乙公司,
当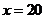 时,选择甲、乙两公司价格一样,
时,选择甲、乙两公司价格一样,
当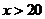 时,选择甲公司
-------------------------11分
时,选择甲公司
-------------------------11分
答:(略)
19.(本小题满分12分)
 证明: (1)在矩形ABCD中,
证明: (1)在矩形ABCD中,
∵AP=PB, DQ=QC,
∴AP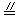 CQ.
CQ.
∴AQCP为平行四边形.
∴CP∥AQ. …………(2分)
∵CP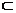 平面CEP,
平面CEP,
AQ 平面CEP,
平面CEP,
∴AQ∥平面CEP. …………(4分)
(2) ∵EP⊥平面ABCD,
AQ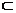 平面ABCD,
平面ABCD,
∴AQ⊥EP. …………(5分)
∵AB=2BC, P为AB中点, ∴AP=AD. 连PQ, ADQP为正方形.
∴AQ⊥DP. 又EP∩DP=P, …………(6分)
∴AQ⊥平面DEP. …………(7分)
∵AQ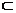 平面AEQ. ∴平面AEQ⊥平面DEP. …………(8分)
平面AEQ. ∴平面AEQ⊥平面DEP. …………(8分)
(3)过P作PO⊥AE, 垂足为O, 连OQ.
∵QP⊥AB, QP⊥EP,
∴QP⊥平面AEP.
则OQ⊥AE.
∴∠QOP为二面角Q-AE-P的平面角. …………(10分)
∵EP=AP=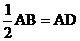 ,
,
∴OP=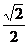 EP=
EP=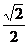 AP=
AP=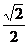 PQ.
PQ.
∴tan∠POQ=arctan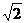 .
.
即二面角Q-AE-P的大小为arctan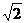 .…………(12分)
.…………(12分)
20.(本小题满分12分)
解: (1)当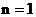 时,
时, 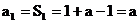 …………(1分)
…………(1分)
当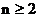 时,
时, 
=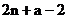 …………(3分)
…………(3分)
可见, 当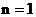 时, 满足上式.
时, 满足上式.
所以, 数列 的通项公式是
的通项公式是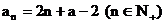 …………(4分)
…………(4分)
(2)由数列 的通项公式是
的通项公式是
可知数列 是等差数列.
是等差数列.
∴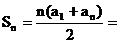
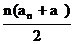 , ∴
, ∴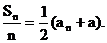 …………(6分)
…………(6分)
∴点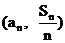 的坐标满足方程
的坐标满足方程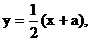
∴点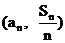 在直线
在直线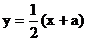 上.
上.
所以, 以集合A中的元素为坐标的点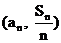 均在直线
均在直线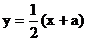 上. …………(8分)
上. …………(8分)
(3)由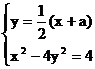 , 消去y, 得
, 消去y, 得 …………①…………(9分)
…………①…………(9分)
当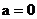 时, 方程①无解,
此时,
时, 方程①无解,
此时, 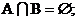 …………(10分)
…………(10分)
当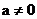 时, 方程①只有一个解
时, 方程①只有一个解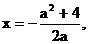
此时方程组也只有一个解, 即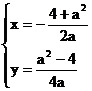
故上述方程组至多有一解, 所以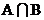 至多有一个元素…………(12分)
至多有一个元素…………(12分)
21.(本小题满分12分)
解: (1) 函数 在区间
在区间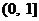 上是增函数, 函数
上是增函数, 函数 在区间
在区间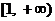 上是减函数.(1分)
上是减函数.(1分)
下面证明: 设 , 则
, 则

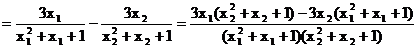
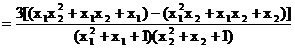
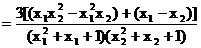
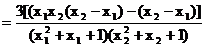
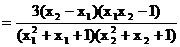 ,…………(3分)
,…………(3分)
∵ ,
,
∴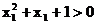 , 同理
, 同理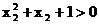 . 又
. 又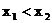 , ∴
, ∴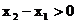 .…………(4分)
.…………(4分)
① 当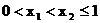 时,
时,  ,
, 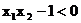 .
.
∴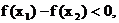 ∴
∴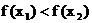 .
.
∴函数 在区间
在区间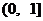 上是增函数.
上是增函数.
②当 时,
时, 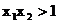 , ∴
, ∴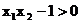 .
.
∴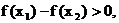 ∴
∴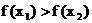 .
.
∴函数 在区间
在区间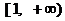 上是减函数.
上是减函数.
综上所述: 函数 在区间
在区间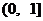 上是增函数, 在区间
上是增函数, 在区间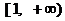 上是减函数. ……(6分)
上是减函数. ……(6分)
(2) 由可知,函数在区间上减函数,
∵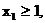
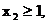 ∴
∴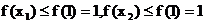 …………(8分)
…………(8分)
又在函数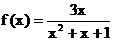 中, ∵3
中, ∵3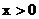 ,
, 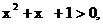
∴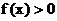 .∴
.∴ ,
, 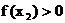 , ∴
, ∴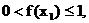
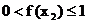 …………(10分)
…………(10分)
∴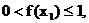
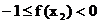 , ∴
, ∴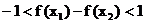 .
.
 ∴
∴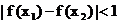 .…………(12分)
.…………(12分)
22.(本小题满分14分)
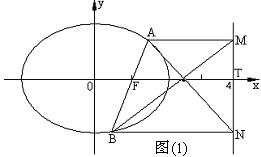
解: (1) 如图(1)
设P点的坐标为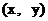 ,
,
则由题设得: ,
,
化简得: 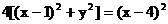 ,
,
即 即
即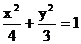 .
.
∴点P的轨迹C的方程是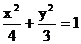 .…………(5分)
.…………(5分)
(2) ①当AB轴时, AB的坐标分别为
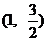 ,
,  ,
,
AN与BM的交点为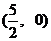 在x轴上. …………(6分)
在x轴上. …………(6分)
②当AB不垂直于x轴时,设直线AB的方程为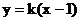 ,
,
代入椭圆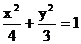 ,得
,得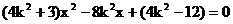 …………(7分)
…………(7分)
设 ,
, 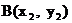 , 则
, 则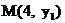 ,
, 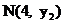 ,
,
且 …………(8分)
…………(8分)
∵直线AN方程是 , 直线BM方程是
, 直线BM方程是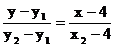 .
.
联列, 得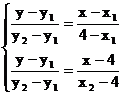 , 消去y, 得:
, 消去y, 得:  .
.
即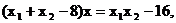 即
即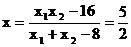 , …………(10分)
, …………(10分)
把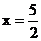 代入直线AN的方程
代入直线AN的方程

得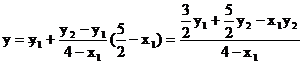
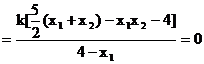 …………(13分)
…………(13分)
∴AN与BM交于点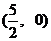 是x轴上一定点. …………(14分)
是x轴上一定点. …………(14分)
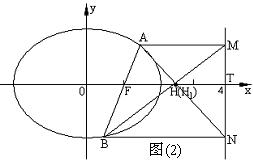 (2) 解法二:
如图(2) 当AB不垂直于x轴时,
(2) 解法二:
如图(2) 当AB不垂直于x轴时,
设AF=n, 则AM=2n, 设BF=m, 则BN=2m,
在△ABN和△BAM中, FH∥AM, FH1∥BN,
∴△ABN∽△AFH和△BAM∽△BFH1
∴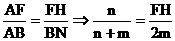

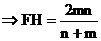 ,…………(10分)
,…………(10分)
同理可推, ∴

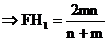 ,
…………(12分)
,
…………(12分)
∴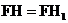 ,∴H与H1重合
,∴H与H1重合
∴AN与BM交点是x轴上一定点. …………(14分)