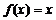1设全集 ,集合
,集合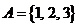 ,
,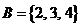 ,则
,则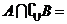 ( )
( )
A 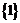 B
B
 C
C
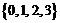 D
D
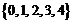
2已知数列 的前
的前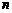 项和为
项和为 ,且
,且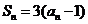 则
则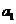 等于 ( )
等于 ( )
A 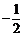 B
B
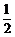 C
C
 D
D
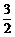
3不等式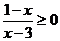 的解集是 ( )
的解集是 ( )
A
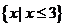 B
B
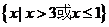 C
C 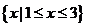 D
D 
4给定两个向量 ,
,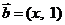 ,若
,若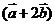 与
与 平行,则x的值等于( )
平行,则x的值等于( )
A 1 B 2 C 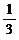 D
D 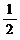
5对于数列 ,“对任意
,“对任意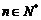 ,点
,点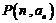 都在直线
都在直线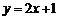 上”是“
上”是“ 为等差数列”的
( )
为等差数列”的
( )
A 充分不必要条件 B 必要不充分条件
C 充要条件 D 既不充分也不必要条件
6已知抛物线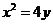 ,则它的焦点坐标是
( )
,则它的焦点坐标是
( )
A 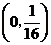 B
B
 C
C
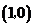 D
D

7若y = x + b与y = ax + 3互为反函数,则 a + b = ( ) A -2 B 2 C 4 D -10
8若要得到函数y=sin(2x- )的图像,可以把函数y=sin2x的图像
( )
)的图像,可以把函数y=sin2x的图像
( )
A 向右平移 个单位
B 向左平移
个单位
B 向左平移 个单位
个单位
C 向左平移 个单位
D 向右平移
个单位
D 向右平移 个单位
个单位
9函数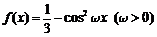 的周期与函数
的周期与函数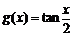 的周期相等,则
的周期相等,则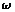 等于 ( )
等于 ( )
A
2 B 1 C 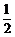 D
D 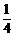
10函数f(q ) = 的最大值和最小值分别是 ( ) A 最大值 和最小值0 B 最大值不存在和最小值
C 最大值 -和最小值0 D 最大值不存在和最小值-
11函数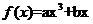 在x=
在x= 处有极值,则
处有极值,则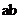 的值为 (
)
的值为 (
)
A 3 B -3 C 0 D 1
12已知数列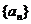 前n项和为
前n项和为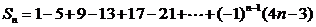 ,
,
则 的值是
( )
的值是
( )
A 13 B -76 C 46 D 76
选择题答案填在下面表格内:
06届南通市小海中学期中考试试卷 2005-11
数学试卷
第Ⅱ卷(非选择题,共90分)
13已知 |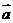 |=1,|
|=1,| |=
|=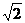 ,若
,若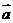 //
// 且
且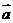 与
与 同向,则
同向,则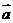 .
. ____________.
____________.
14已知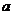 为实数,
为实数,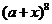 展开式中
展开式中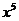 的系数为
的系数为 ,则
,则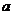 =____________.
=____________.
15 在 中,
中,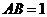
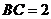 ,
, ,则
,则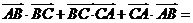 _______.
_______.
16在数列 中,
中, ,
, ,则数列{an}的通项公式
,则数列{an}的通项公式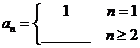
17 (本小题满分12分)
已知等比数列 中,
中, ,
, .
.
(I) 求通项 ;
;
(II) 若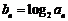 ,
,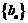 数列的前
数列的前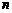 项和为
项和为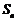 ,且
,且 ,求
,求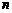 的值.
的值.
18 (本小题满分12分)
从10个元件中(其中4个相同的甲品牌元件和6个相同的乙品牌元件)随机选出3个参加某种性能测试 每个甲品牌元件能通过测试的概率均为
每个甲品牌元件能通过测试的概率均为 ,每个乙品牌元件能通过测试的概率均为
,每个乙品牌元件能通过测试的概率均为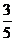
 试求:
试求:
(I)选出的3个元件中,至少有一个甲品牌元件的概率;
(II)若选出的三个元件均为乙品牌元件,现对它们进行性能测试,求至少有两个乙品牌元件同时通过测试的概率
19 (本小题满分12分)
已知向量 =(sinB,1-cosB),且与向量
=(sinB,1-cosB),且与向量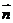 =(2,0)的夹角为
=(2,0)的夹角为 ,其中A, B, C是
,其中A, B, C是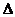 ABC的内角.
ABC的内角.
(I)求角B的大小; (II)求sinA+sinC的取值范围.
20 (本小题满分12分)
已知函数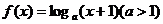 ,若函数
,若函数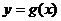 图象上任意一点P关于原点的对称点Q的轨迹恰好是函数
图象上任意一点P关于原点的对称点Q的轨迹恰好是函数 的图象
的图象
(1)写出函数 的解析式;
的解析式;
(2)当 时,总有
时,总有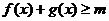 成立,求实数
成立,求实数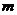 的取值范围
的取值范围
21 (本小题满分12分)
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方体,PD=CD=2,E、F分别是AB、PB的中点
(1)求证:EF⊥CD;
(2)求DB与平面DEF所成角的大小;
(3)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论

22 (本小题满分14分)
设 ,函数
,函数 的定义域为
的定义域为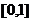 ,且
,且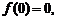
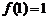 ,对定义域内任意的
,对定义域内任意的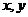 ,满足
,满足 ,
,
求:(1)  及
及 的值; (2)函数
的值; (2)函数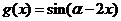 的单调递增区间;
的单调递增区间;
(3) 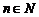 时,
时, ,求
,求 ,并猜测
,并猜测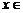
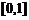 时,
时, 的表达式
的表达式
06届南通市小海中学期中考试试卷 2005-11
06届南通市小海中学期中考试试卷 2005-11 数学试卷(普通班) 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分 第Ⅰ卷1页至2页,第Ⅱ卷3至6页 共150分,考试时间120分钟 第Ⅰ卷(选择题 共60分) 参考公式: 如果事件A、B互斥,那么 球的表面积公式 P(A+B)=P(A)+P(B) S球=4πR2 如果事件A、B相互独立,那么 参考答案
数学试卷参考答案
选择题(每小题5分,共计60分)
ADDDA DCACA BB
二、填空题(每小题4分,共计16分)
13.
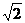 14.
14. 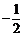 15. -5 16.
15. -5 16.

三、解答题(本题共6小题,共计74分)
17 解:(Ⅰ) 设等比数列 的公比为
的公比为 ,则
,则
 ………………………………………………………………2分
………………………………………………………………2分
解之得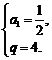 .………………………………………………………………4分
.………………………………………………………………4分
∴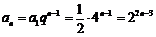 .………………………………………………6分
.………………………………………………6分
(Ⅱ) 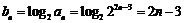 .……………………………………………8分
.……………………………………………8分
∵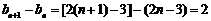 ,
,
∴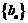 是首项为
是首项为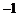 ,公差为2的等差数列.
,公差为2的等差数列.
∴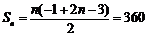 .…………………………………………………10分
.…………………………………………………10分
∴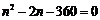 ,∴
,∴ 或
或 (舍去).…………………………………12分
(舍去).…………………………………12分
18.解:(Ⅰ)随机选出的3个元件中,至少有一个甲品牌元件的概率为
1- ;………………6分
;………………6分
(Ⅱ)至少有两个乙品牌元件同时通过测试的概率为
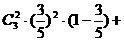
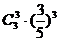 =
=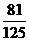 ;………………12分
;………………12分
答:略
19.解:(1)∵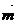 =(sinB,1-cosB) , 且与向量
=(sinB,1-cosB) , 且与向量 (2,0)所成角为
(2,0)所成角为
∴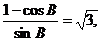 ……………………………………………………………………3’
……………………………………………………………………3’
∴tan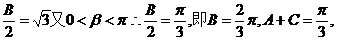 ……………………6’
……………………6’
第一问:另解:∵  , 且与向量
, 且与向量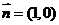 所成角为
所成角为
∴
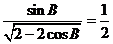 ,……………………………………………………………3’
,……………………………………………………………3’
∴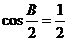 ,又
,又 ,∴
,∴ 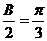 ,即
,即
 ………………6’
………………6’
(2):由(1)可得∴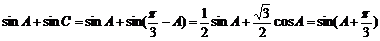
………………………………………………8’
∵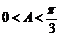
∴ ……………………………………………………………………10’
……………………………………………………………………10’
∴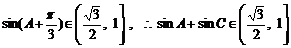
当且仅当 …………………………………………12’
…………………………………………12’
20.解:(1)设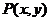 ,则
,则

∵
 在函数
在函数 的图象上
的图象上
∴
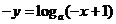 ,即
,即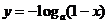 ,
,
这就是说, …………………………………4分
…………………………………4分
(2)当 ,
,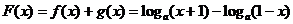
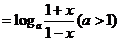 …………………6分
…………………6分
由题意知,只要

∵
 在
在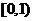 上是增函数
上是增函数
∴
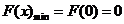 ,故
,故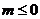 即为所求
即为所求 …………………12分
…………………12分
21、(满分12分)
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方体,PD=CD,E、F分别是AB、PB的中点
(1)求证:EF⊥CD;
(2)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论;
(3)求DB与平面DEF所成角的大小
解:以DA、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系(如图),
则D(0,0,0)、A(2,0,0)、
B(2,2,0)、C(0,2,0)、
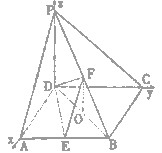 E(2,1,0)、F(1,1,1)、
E(2,1,0)、F(1,1,1)、
P(0,0,2)…………2分
(1)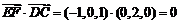
∴EF⊥DC …………4分
(2)设平面DEF的法向量为
由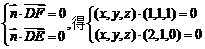
即
∴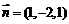 …………………………………………6分
…………………………………………6分

∴ DB与平面DEF所成角大小
为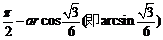 …………………………8分
…………………………8分
(3)设G(x,0,z),则G∈平面PAD
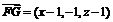

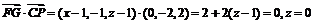
∴G点坐标为(1,0,0),
即G点为AD的中点 …………………………………12分
22 解:(1)
解:(1) ,
,
 ,
,
 ,
,
 ,
,
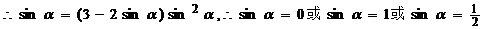 ,
,


第一问:另解:
 ,
,

又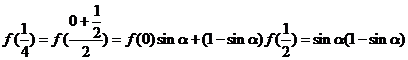
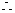
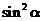
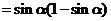
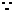
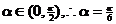
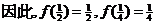
(2) ,
,
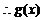 的增区间为
的增区间为

(3)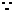
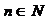 ,
,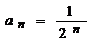 ,
,
所以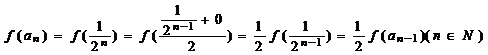 ,
,
因此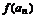 是首项为
是首项为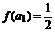 ,公比为
,公比为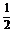 的等比数列,故
的等比数列,故 ,
,
猜测