
1.设集合U={0,1,2,3,4,5},集合M={0,3,5},N={1,4,5},则
(A){5} (B){0,3} (C){0,2,3,5} (D) {0,1,3,4,5}
2.求复数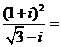
(A) (B)
(B)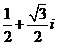 (C)
(C)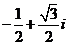 (D)
(D)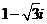
3.已知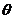 是锐角,那么下列各值中,
是锐角,那么下列各值中,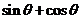 能取到的值是
能取到的值是
(A) (B)
(B)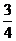 (C)
(C)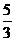 (D)
(D)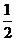
4.若命题甲的逆命题是乙,命题甲的否命题是丙,则命题乙是命题丙的
(A)逆命题 (B)逆否命题 (C)否命题 (D)否定
5.函数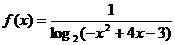 的定义域为
的定义域为
(A)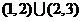 (B)
(B) (C)(1,3)
(D)[1,3]
(C)(1,3)
(D)[1,3]
6.已知直线m、n,平面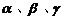 ,则
,则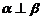 的一个充分不必要条件为
的一个充分不必要条件为
(A)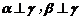 (B)
(B) (C)
(C)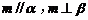 (D)
(D)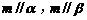
7.设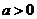 ,不等式
,不等式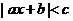 的解集是
的解集是 ,则
,则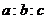 等于
等于
(A)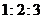 (B)
(B)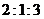 (C)
(C)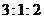 (D)
(D)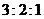
8.等差数列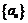 中,若
中,若 ,则
,则 的值为:
的值为:
(A)10 (B)11 (C)12 (D)14
9. 的图象是:
的图象是:
(A)关于原点成中心对称
(B)关于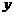 轴成轴对称
轴成轴对称
(C)关于点 成中心对称
(D)关于直线
成中心对称
(D)关于直线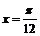 成轴对称
成轴对称
10.在R上定义运算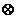 :x
:x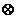 y=x(1-y).若不等式(x-a)
y=x(1-y).若不等式(x-a)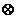 (x+a)<1对任意实数x成立,则
(x+a)<1对任意实数x成立,则
A.-1<a<1 B.0<a<2 C.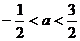 D.
D.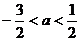
11.在重庆召开的“市长峰会”期间,某高校有14名志愿者参加接待工作.若每天排早、中、晚三班,每班4人,每人每天最多值一班,则开幕式当天不同的排班种数为
(A)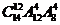 (B)
(B) (C)
(C)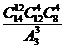 (D)
(D)
12. 定义在R上的偶函数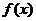 满足
满足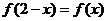 ,且在[-3,-2]上是减函数,
,且在[-3,-2]上是减函数, 是钝角三角形的两个锐角,则下列不等式关系中正确的是
是钝角三角形的两个锐角,则下列不等式关系中正确的是
(A)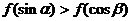 (B)
(B)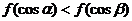
(C)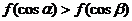 (D)
(D)
13.若 ,则常数
,则常数 的值分别为 。
的值分别为 。
14.函数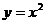 的图象F按向量a
的图象F按向量a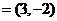 平移到G,则图象G的函数解析式为
。
平移到G,则图象G的函数解析式为
。
15.在 的展开式中,常数项是 。
的展开式中,常数项是 。
16.已知函数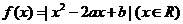 .给出下列命题:①
.给出下列命题:①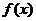 必是偶函数;②当
必是偶函数;②当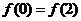 时,
时,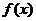 的图像必关于直线x=1对称;③若
的图像必关于直线x=1对称;③若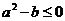 ,则
,则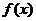 在区间
在区间 上是增函数;④
上是增函数;④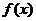 有最大值
有最大值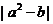 . 其中正确的序号是________。
. 其中正确的序号是________。
17.在教室内有10个学生,分别佩带着从1号到10号的校徽,任意取3人记录其校徽的号码。
(1)求最小号码为5的概率。
(2)求3个号码中至多有一个是偶数的概率。
(3)求3个号码之和不超过9的概率。
18.在△ABC中,a,b,c分别为角A,B,C的对边,设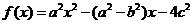 ,
,
(1)若 ,且B-C=
,且B-C= ,求角C.
,求角C.
(2)若 ,求角C的取值范围.
,求角C的取值范围.
19.(已知数列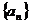 的前n项和为
的前n项和为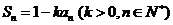 .(1)用k、n表示
.(1)用k、n表示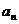 ;
;
(2)数列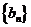 对于任意正整数n都有
对于任意正整数n都有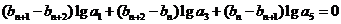 ,
,
求证:数列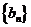 为等差数列;
为等差数列;
20.定义在R上的函数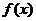 满足
满足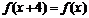 ,当2≤x≤6时,
,当2≤x≤6时,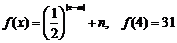 。
。
(1)求m ,n的值;
(2)比较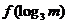 与
与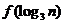 的大小
的大小
21、(本题满分14分)已知定点A(1,0)和直线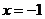 上的两个动点E、F且
上的两个动点E、F且 ,动点
,动点 满足
满足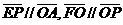 (其中O为坐标原点)。
(其中O为坐标原点)。
(Ⅰ)求动点 的轨迹C的方程;
的轨迹C的方程;
(Ⅱ)过点B(0,2)的直线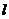 与(Ⅰ)中轨迹C相交于两个不同的点M、N,若
与(Ⅰ)中轨迹C相交于两个不同的点M、N,若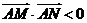 ,求直线
,求直线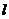 的斜率的取值范围。
的斜率的取值范围。
22.(本题满分14分)
设x1,x2是函数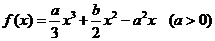 的两个极值点,且
的两个极值点,且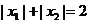 。
。
(1) 用a表示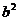 ,并求出a的取值范围.
,并求出a的取值范围.
(2) 证明: 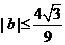 .
.
(3) 若函数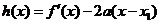 ,证明:当
,证明:当 且x1<0时,
且x1<0时, 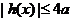 .
.
眉山市高中2006届第一次诊断考试 数学(理工农医类) 2005.12 4.参考公式: 如果事件A、B互斥,那么。 如果事件A、B相互独立,那么 如果事件A在一次试验中发生的概率是p,那么n次独立重复试验中恰好发生k次的概率为参考答案
眉山市高中2006届第一次诊断考试数学(理)参考答案
2005.12.27
一、选择题:BC ABAC BCDC BD
1.解:∵U={0,1,2,3,4,5} ,M={0,3,5},N={1,4,5};
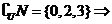
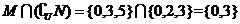 故选B
故选B
2.解: 故选C
故选C
3.解:利用排除法。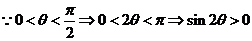 ,而B、D的
,而B、D的 ;
;
C的 ,不符合有界性。
故选A
,不符合有界性。
故选A
4.解:若甲: ;则乙
;则乙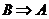 ;则丙:
;则丙: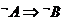 ;故乙是丙的逆否命题。故选B
;故乙是丙的逆否命题。故选B
5.解: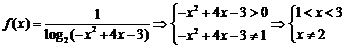 故选A
故选A
6.解:当“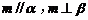 ”为条件时可推出结论“
”为条件时可推出结论“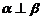 ”成立;
”成立;
当“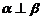 ”成立时,m与
”成立时,m与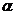 、m与
、m与 的位置关系不确定。
故选C
的位置关系不确定。
故选C
7.解: 的解是:
的解是:
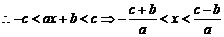 ,则
,则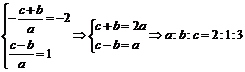 故选B
故选B
8.解:因为数列{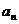 }为等差数列,设公差为d., 若
}为等差数列,设公差为d., 若 ,
,
又因为:
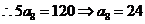
而 故选C
故选C
9.解:因为 若是关于中心对称:
若是关于中心对称:
则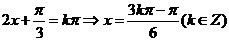 ,故
,故 ,所以不关于指定的点成中心对称;
,所以不关于指定的点成中心对称;
若是关于轴对称:则
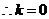 时,对称轴为
时,对称轴为
10.解:因定义运算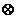 :x
:x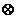 y=x(1-y) ,所以不等式(x-a)
y=x(1-y) ,所以不等式(x-a)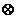 (x+a)<1
(x+a)<1
即 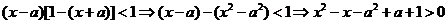
又因为对一切x都成立,所以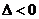 ,即
,即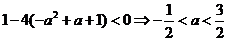
11.解:有14名志愿者,但每天早、中、晚三班,每班4人,只需12人,所以应先从14人中选出12人,然后这12人再来分组排班。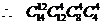 故选B
故选B
12.解: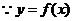 是偶函数,且在
是偶函数,且在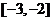 上是减函数,所以在
上是减函数,所以在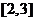 上是增函数;
上是增函数;
又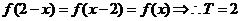
故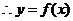 在
在 上是增函数;
上是增函数;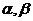 是钝角三角形的两个锐角,
是钝角三角形的两个锐角,
 ,
,
而 所以:
所以:
二、填空题:
13. ;
;
解: ,
,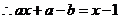

14.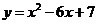
解: 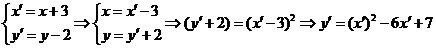
15.-252
解: 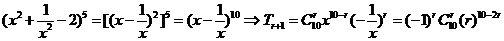

16.③
解:①不恒为偶函数;
②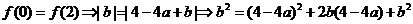 ,
,
所以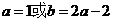 ,若
,若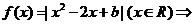 关于
关于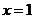 对称,
对称,
若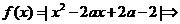 不恒关于
不恒关于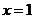 对称;
对称;
③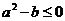 时,整个图象在x轴的上方(或顶点在x轴上)
时,整个图象在x轴的上方(或顶点在x轴上)
 ,故
,故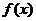 在区间
在区间 上是增函数;
上是增函数;
④无最大值。(开口向上)
三、解答题
17.解:(1)从10人中任取3人,共有 种,最小号码为5,相当于从6,7,8,9,10共五个中任取2个,则共有
种,最小号码为5,相当于从6,7,8,9,10共五个中任取2个,则共有 种结果.则最小号码为5的概率为P=
种结果.则最小号码为5的概率为P=  =
= ………………(4分).
………………(4分).
(2)选出3个号码中至多有一个是偶数,包括没有偶数和恰有一个偶数两种情况,共有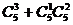 种.所以满足条件的概率为P=
种.所以满足条件的概率为P=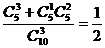 ……(8分)
……(8分)
(3)3个号码之和不超过9的可能结果有:
(1,2,3)、(1,2,4)、(1,2,5)、(1,2,6)、(2,3,4)、(1,3,4)、(1,3,5)
则所求概率为. P= 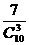 =
= ………………(12分).
………………(12分).
18.解;(1)由f(1)=0,得a2-a2+b2-4c2=0, ∴b= 2c…………(1分).
又由正弦定理,得b= 2RsinB,c=2RsinC,将其代入上式,得sinB=2sinC…………(2分)
∵B-C= ,∴B=
,∴B= +C,将其代入上式,得sin(
+C,将其代入上式,得sin( +C)=2sinC……………(3分)
+C)=2sinC……………(3分)
∴sin( )cosC + cos
)cosC + cos  sinC =2sinC,整理得,
sinC =2sinC,整理得,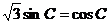 …………(4分)
…………(4分)
∴tanC=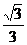 ……………(5分)
……………(5分)
∵角C是三角形的内角,∴C= …………………(6分)
…………………(6分)
(2)∵f(2)=0,∴4a2-2a2+2b2-4c2=0,即a2+b2-2c2=0……………(7分)
由余弦定理,得cosC= ……………………(8分)
……………………(8分)
=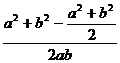 ∴cosC=
∴cosC=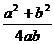
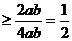 (当且仅当a=b时取等号)……(10分)
(当且仅当a=b时取等号)……(10分)
∴cosC≥ ,∠C是锐角,又∵余弦函数在(0,
,∠C是锐角,又∵余弦函数在(0, )上递减,∴.0<C≤
)上递减,∴.0<C≤ ………(12分)
………(12分)
19.解:(1) 时,
时,
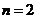 时,
时, …………3分
…………3分
 数列
数列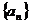 为等比数列, ………………4分
为等比数列, ………………4分
 ,……………………………………………………5分
,……………………………………………………5分
(2)由题意知:
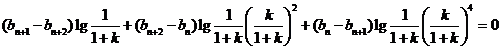

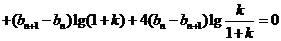 ………………8分
………………8分

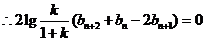
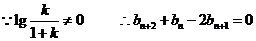
即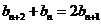 , 故数列
, 故数列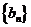 为等差数列。
……………………12分
为等差数列。
……………………12分
20.解:(1)∵f(x)在R上满足f (x+4)=f (x),∴4是f(x)的一个周期.∴f (2)= f (6)…(2分)
∴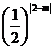 +n=
+n=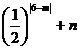 ①,
①,
又∵f (4)=31,∴ +n=31 ② ……………(4分)
+n=31 ② ……………(4分)
联解①、②组成的方程组,得m =4,n=30…………………(6分).
(2)由(1)知,f(x)= +30,x∈
+30,x∈ .
.
∵1<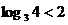 , ∴5<
, ∴5< .∴f(log3 m)= f(log3 4)=f(
.∴f(log3 m)= f(log3 4)=f(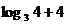 )
)
=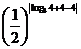 =
=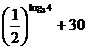 ……………………………(8分)
……………………………(8分)
又∵3< ,∴f(log3 n)= f(log3 30)=
,∴f(log3 n)= f(log3 30)=
=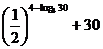 =
= …………………(10分)
…………………(10分)
∵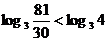 ,∴
,∴
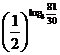
∴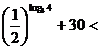
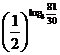 +30,∴f(log3 m)<f(log3 n)………(12分).
+30,∴f(log3 m)<f(log3 n)………(12分).
21.(I)设 (
( 、
、 均不为)
均不为)
由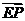 //
// 得
得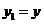 ,即
,即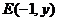
 (2分)
(2分)
由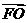 //
// 得
得 ,即
,即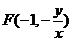
 (4分)
(4分)
由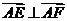 得
得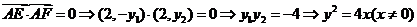
 动点
动点 的轨迹
的轨迹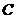 的方程为
的方程为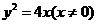
 (6分)
(6分)
(II)设直线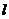 的方程为
的方程为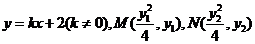
联立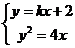 消去
消去 得
得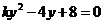
 ,
,
 (8分)
(8分)
且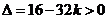 即
即 ①
①
 (9分)
(9分)
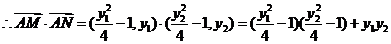
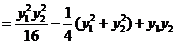

 (12分)
(12分)
 ②
②
综合①②知直线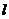 的斜率的取值范围为
的斜率的取值范围为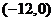
 (13分)
(13分)
22.解:(1)∵f (x )
= x3 +
x3 + 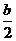 x2–a2 x,∴f 1(x ) = a x2
+ bx–a2
…………(1分)
x2–a2 x,∴f 1(x ) = a x2
+ bx–a2
…………(1分)
∵x1 ,x 2是f (x )的两个极值点,∴x1 ,x 2是方程a x2 + bx–a2=0的两个实根…(2分)
∵a > 0 ,∴x1 x 2=- a2 ,x1 +x 2=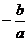 ,∴︱x1︱+︱x 2︱=︱x1
- x 2 ︱=
,∴︱x1︱+︱x 2︱=︱x1
- x 2 ︱=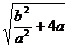 =2,
=2,
∴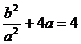 ,∴b2 = 4a2 -4a3 ……………………(4分)
,∴b2 = 4a2 -4a3 ……………………(4分)
∵b2≥0 ,∴4a2 -4a3≥0 ,∴0<a≤1…………………………(5分)
(2)∵b2
= 4a2 -4a3 (0<a≤1),令g(a)= 4a2 -4a3 ,∴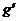 (a
) =8 a–12a2…(6分)
(a
) =8 a–12a2…(6分)
由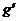 (a) >0 ,得0<a<
(a) >0 ,得0<a<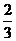 , 由
, 由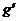 (a) <0 ,得
(a) <0 ,得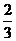 <a≤1.
<a≤1.
∴g(a)在(0
, 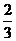 )上递增,在(
)上递增,在(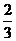 ,1)上递减.……………………………(8分)
,1)上递减.……………………………(8分)
∴g(a)在(0
,1)上的最大值是g(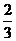 )=
)=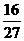 .
.
∴g(a) ≤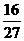 .∴
b2≤
.∴
b2≤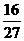 .∴
∣b︱≤
.∴
∣b︱≤ ……(9分)
……(9分)
(3)∵x1 ,x 2是方程a x2 + bx–a2=0的两个实根,∴f 1(x ) = a(x–x1)(x-x 2).
∴h(x ) = a(x–x1)(x-x 2)-2a(x–x1)= a(x–x1)(x-x 2-2)………(10分)
∴∣h(x )∣=
a∣x–x1∣∣x-x 2-2∣≤ ……(11分)
……(11分)
∵x>x1 ,∴x–x1>0. 又∵x1<0,∴x1 x 2<0 ,∴ x 2>0 .∴ x 2+2>2 .
又∵x<2,∴x-x 2-2<0 ……………………………………………(12分)
∴∣h(x )∣≤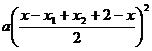 =
=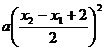 .
.
又∵∣x1∣+∣x2∣=2,且x1<0, x 2>0 ,∴ x 2-x1=2 .
将其代入上式得∣h(x )∣≤4a.………………………………………(13分)