
1. 已知函数y=f(x)(a≤x≤b),则集合{(x,y)| y=f(x),a≤x≤b}∩{(x,y)|x=0}中含有元素的个数为( )
A.0 B.1或0 C.1 D.1或2
2. 设函数f(x)=logax(a>0且a≠1)满足f(9)=2,则f-1(loga2)等于( )
A.2 B.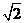 C.
C.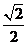 D.log2
D.log2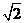
3. 函数y=ln(1+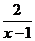 ),x∈(1,+∞)的反函数为( )
),x∈(1,+∞)的反函数为( )
A.y=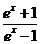 ,x∈(0,+∞) B.y=
,x∈(0,+∞) B.y=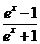 ,x∈(0,+∞)
,x∈(0,+∞)
C.y=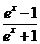 ,x∈(-∞,0) D.y=
,x∈(-∞,0) D.y=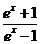 ,x∈(-∞,0)
,x∈(-∞,0)
4. 设a>0,a≠1,函数y=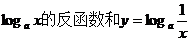 的反函数的图象关于( )
的反函数的图象关于( )
A.x轴对称 B.y轴对称 C.y=x对称 D.原点对称
5. 函数f(x)=|2x-1|,若a<b<c且f(a)>f(c)>f(b),则下列四个式子是成立的是( )
A.a<0,b<0,c<0 B.a<0,b≥0,c>0 C.2-a<2c D.2c+2a<2
6. 当x∈(-2,-1)时,不等式(x+1)2<loga|x|恒成立,则实数a的取值范围是( )
A.[2,+∞) B.(1,2] C.(1,2) D.(0,1)
7. 函数f(x)=x2+ax-3a-9对任意x∈R恒有f(x)≥0,则f(1)=( )
A.6 B.5 C.4 D.3
8. 关于x的方程ax=-x2+2x+a(a>0,且a≠1)的解的个数是( )
A.1 B.2 C.0 D.视a的值而定
9. f(x)是定义域为R的增函数,且值域为R+,则下列函数中为减函数的是( )
A.f(x)+ f(-x) B.f(x)-f(-x) C.f(x).f(-x) D.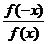
10.f(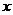 )是定义在区间[-c,c]上的奇函数,其图象如图所示:令g(x)=af(x)+b,则下列关于函数g(x)的叙述正确的是( )
)是定义在区间[-c,c]上的奇函数,其图象如图所示:令g(x)=af(x)+b,则下列关于函数g(x)的叙述正确的是( )
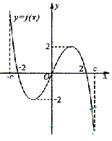 A.若a<0,则函数g(x)的图象关于原点对称.
A.若a<0,则函数g(x)的图象关于原点对称.
B.若a=-1,-2<b<0,则方程g(x)=0有大于2的实根.
C.若a≠0,b=2,则方程g(x)=0有两个实根.
D.若a≥1,b<2,则方程g(x)=0有三个实根.
11.设lg2x-lgx2-2=0的两根是a、b,则logab+logba的值是( )
A.-4 B.-2 C.1 D.3
12.如图所示, 是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的x1和x2,任意
是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的x1和x2,任意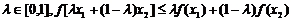 恒成立”的只有
恒成立”的只有
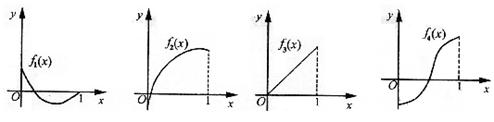
A.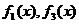 B.
B.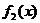 C.
C.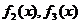 D.
D.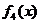
13.已知函数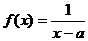 的反函数
的反函数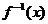 的图象的对称中心是(0,2),则a= 。
的图象的对称中心是(0,2),则a= 。
14.函数f(x)=lg(1+x2),g(x)=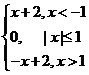 ,h(x)=tan2x中, 是偶函数。
,h(x)=tan2x中, 是偶函数。
15.已知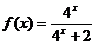 ,则和
,则和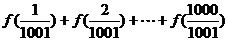 =
。
=
。
16.设函数f(x)=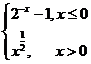 ,若f(x0)>1,则x0的取值范围是 。
,若f(x0)>1,则x0的取值范围是 。
17.已知a>0,b>0,x∈R且M=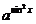 .
.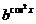 ,N=a+b,试比较M与N的大小,并说明理由。
,N=a+b,试比较M与N的大小,并说明理由。
18.已知f(x)=x2-x+k,若log2f(a)=2且f(log2a)=k(a>0且a≠1)。
⑴确定k的值;
⑵求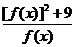 的最小值及对应的x值。
的最小值及对应的x值。
19.已知函数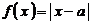 ,
,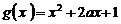 (
(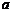 为正常数),且函数
为正常数),且函数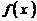 与
与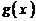 的图象在
的图象在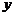 轴上的截距相等。
轴上的截距相等。
⑴求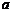 的值;
的值;
⑵求函数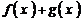 的单调递增区间。
的单调递增区间。
20.设函数f(x)的定义域是R,对于任意实数m,n,恒有f(m+n)=f(m)f(n),且当x>0时,0<f(x)<1。
⑴求证:f(0)=1,且当x<0时,有f(x)>1;
⑵判断f(x)在R上的单调性;
⑶设集合A={(x,y)|f(x2)f(y2)>f(1)},集合B={(x,y)|f(ax-y+2)=1,a∈R},若A∩B=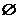 ,求a的取值范围。
,求a的取值范围。
21.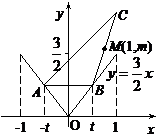 如图,函数y=
如图,函数y=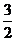 |x|在x∈[-1,1]的图象上有两点A,B,AB∥Ox轴,点M(1,m)(m是已知实数,且m>
|x|在x∈[-1,1]的图象上有两点A,B,AB∥Ox轴,点M(1,m)(m是已知实数,且m>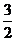 )是△ABC的边BC的中点。
)是△ABC的边BC的中点。
⑴写出用B的横坐标t表示△ABC面积S的函数解析式S=f(t);
⑵求函数S=f(t)的最大值,并求出相应的C点坐标。
22.设y=f(x)是定义在区间[-1,1]上的函数,且满足条件:
(i)f(-1)=f(1)=0;
(ii)对任意的u,v∈[-1,1],都有|f(u)-f(v)|≤|u-v|。
⑴证明:对任意的x∈[-1,1],都有x-1≤f(x)≤1-x;
⑵证明:对任意的u,v∈[-1,1],都有|f(u)-f(v)|≤1;
⑶在区间[-1,1]上是否存在满足题设条件的奇函数y=f(x),且使得
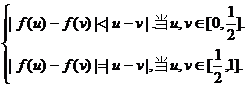
若存在,请举一例:若不存在,请说明理由.
高三单元试题之二函数参考答案
高三单元试题之二:函数参考答案
一、1.B 2.B 3.A 4.B 5.D 6.B 7.C 8.B 9.D 10.B 11.A 12.A
二、13.2 14.f(x),g(x) 15.500 16.(-∞,-1)∪(1,+∞)
三、17.解: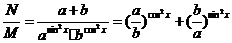 。
。
①
若a>b>0,则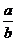 >1,0<
>1,0<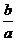 <1。由指数函数的性质知
<1。由指数函数的性质知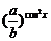 ≥1,0<
≥1,0<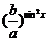 ≤1,∴
≤1,∴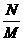 >1,于是N>M;
>1,于是N>M;
②
若a=b>0,则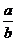 =
=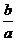 =1,∴
=1,∴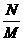 =
=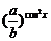 +
+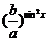 =1+1>1,于是N>M;
=1+1>1,于是N>M;
③ 若0<a<b,同理有N>M。综上所述N>M。
18.解:⑴由题设有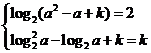 ,∴
,∴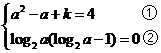
∵a≠1,∴log2a≠0,由②得log2a-1=0,∴a=2,代入①解得k=2。
⑵∵k=2,∴f(x)=x2-x+2=(x- )2+
)2+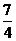 >0。
>0。
∴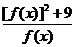 =f(x)+
=f(x)+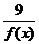 ≥
≥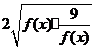 =6。当且仅当f(x)=
=6。当且仅当f(x)=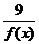 ,即[f(x)]2=9时取等号。∵f(x)>0,∴f(x)=3时取等号。即x2-x+2=3,解得x=
,即[f(x)]2=9时取等号。∵f(x)>0,∴f(x)=3时取等号。即x2-x+2=3,解得x=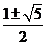 。当x=
。当x=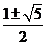 时,
时,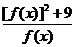 取最小值。
取最小值。
19.解:⑴由题意,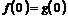 ,
,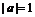 又
又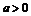 ,所以
,所以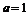 。
。
⑵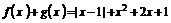
当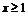 时,
时,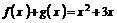 ,它在
,它在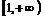 上单调递增;
上单调递增;
当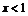 时,
时,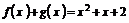 ,它在
,它在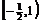 上单调递增。
上单调递增。
20.解:⑴f(m+n)=f(m)f(n),令m=1,n=0,则f(1)=f(1)f(0),且由x>0时,0<f(x)<1,∴f(0)=1;设m=x<0,n=-x>0,∴f(0)=f(x)f(-x),∴f(x)=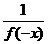 >1。
>1。
⑵设x1<x2,则x2-x1>0,∴0<f(x2-x1)<1,∴f(x2)-f(x1)=f[(x2-x1)+x1]-f(x1)=f(x2-x1)f(x1)-f(x1)=f(x1)[f(x2-x1)-1]<0,∴f(x)在R上单调递减。
⑶∵f(x2)f(y2)>f(1),∴f(x2+y2)>f(1),由f(x)单调性知x2+y2<1,又f(ax-y+2)=1=f(0),
∴ax-y+2=0,又A∩B=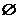 ,∴
,∴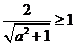 ,∴a2+1≤4,从而
,∴a2+1≤4,从而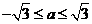 。
。
21.解:⑴依题意,设B(t, 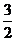 t),A(-t,
t),A(-t, 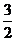 t)(t>0),C(x0,y0)。∵M是BC的中点,∴
t)(t>0),C(x0,y0)。∵M是BC的中点,∴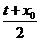 =1,
=1,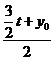 =m,∴x0=2-t,y0=2m-
=m,∴x0=2-t,y0=2m-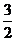 t。在△ABC中,|AB|=2t,AB边上的高h=y0-
t。在△ABC中,|AB|=2t,AB边上的高h=y0-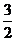 t=2m-3t。∴S=
t=2m-3t。∴S= |AB|.h=
|AB|.h= .2t.(2m-3t)=-3t2+2mt,t∈(0,1]。
.2t.(2m-3t)=-3t2+2mt,t∈(0,1]。
⑵S=-3t2+2mt=-3(t-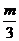 )2+
)2+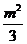 ,t∈(0,1]。若
,t∈(0,1]。若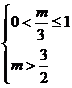 ,即
,即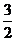 <m≤3。当t=
<m≤3。当t=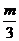 时,Smax=
时,Smax=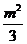 ,相应的C点坐标是(2-
,相应的C点坐标是(2-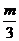 ,
,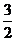 m)。若
m)。若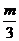 >1,即m>3时,S=f(t)在区间(0,1]上是增函数,∴Smax=f(1)=2m-3,相应的C点坐标是(1,2m-
>1,即m>3时,S=f(t)在区间(0,1]上是增函数,∴Smax=f(1)=2m-3,相应的C点坐标是(1,2m-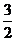 )。
)。
22.⑴证明:由题设条件可知,当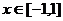 时,有
时,有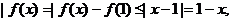
即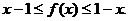
⑵证法一:对任意的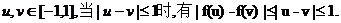
当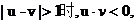 不妨设
不妨设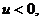 则
则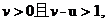
所以,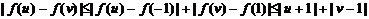
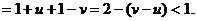 综上可知,对任意的
综上可知,对任意的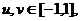 都有
都有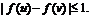
证法二:由⑴可得,当
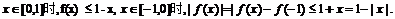
所以,当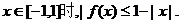 因此,对任意的
因此,对任意的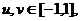
当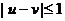 时,
时,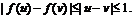 当
当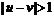 时,有
时,有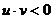
且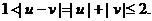
所以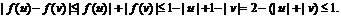
综上可知,对任意的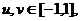 都有
都有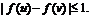
⑶答:满足所述条件的函数不存在.
理由如下,假设存在函数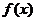 满足条件,则由
满足条件,则由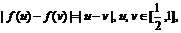
得 又
又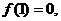 所以
所以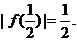 ①
①
又因为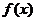 为奇数,所以
为奇数,所以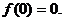 由条件
由条件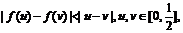
得 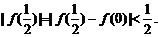 ② ①与②矛盾,所以假设不成立,即这样的函数不存在.
② ①与②矛盾,所以假设不成立,即这样的函数不存在.