
高考复习上海市闵行三中高三数学期末强化卷(三)参考答案
2005年上海市高三数学十校联考试卷(理科)(解答)
(南模、复兴、上外、复旦附中、延安、华东师大二附中、上海、上师大附中、交大附中、向明)
一、填空题:
1、若集合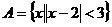 ,集合
,集合 ,则
,则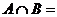
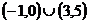 。
。
2、函数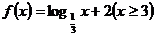 的反函数的定义域是
的反函数的定义域是
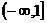 。
。
3、已知椭圆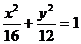 的左焦点是
的左焦点是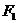 ,右焦点是
,右焦点是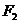 ,点
,点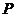 在椭圆上,如果线段
在椭圆上,如果线段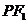 的中点在
的中点在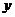 轴上,那么
轴上,那么
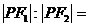
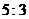 。
。
4、化简: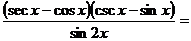
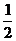 。
。
5、已知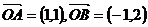 ,以
,以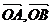 为边作平行四边形
为边作平行四边形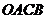 ,则
,则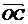 与
与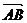 的夹角为
的夹角为
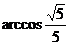 。
。
6、在集合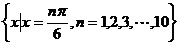 中任取一个元素,所取元素恰好满足方程
中任取一个元素,所取元素恰好满足方程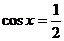 的概率是
的概率是
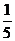 。
。
 7、正方体
7、正方体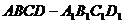 中,与
中,与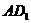 异面,且与
异面,且与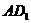 所成角为
所成角为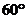
的面对角线共有
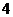 条。
条。
8、曲线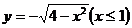 的长度是
的长度是
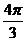 。
。
9、若复数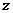 满足
满足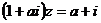 ,且
,且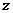 在复平面内所对应的点位于
在复平面内所对应的点位于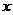 轴的上方,则实数
轴的上方,则实数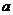 的取值范围是
的取值范围是
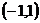 。
。
10、一质点在直角坐标平面上沿直线匀速行进,上午7时和9时该动点的坐标依次为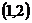 和
和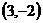 ,则下午5时该
,则下午5时该
点的坐标是
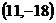 。
。
11、若对任意实数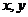 都有
都有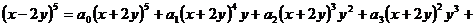
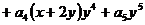 ,则
,则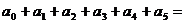
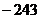 。
。
12、对于各数互不相等的正数数组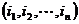 (
(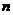 是不小于
是不小于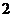 的正整数),如果在
的正整数),如果在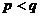 时有
时有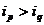 ,则称
,则称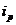 与
与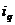 是该数组的一个“逆序”,一个数组中所有“逆序”的个数称为此数组的“逆序数”。例如,数组
是该数组的一个“逆序”,一个数组中所有“逆序”的个数称为此数组的“逆序数”。例如,数组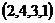 中有逆序“2,1”,“4,3”,“4,1”,“3,2”,其“逆序数”等于4。若各数互不相等的正数数组
中有逆序“2,1”,“4,3”,“4,1”,“3,2”,其“逆序数”等于4。若各数互不相等的正数数组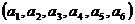 的“逆序数”是2,则
的“逆序数”是2,则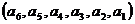 的“逆序数”是
的“逆序数”是
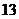 。
。
二、选择题:
13、若角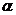 和
和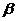 的始边都是
的始边都是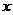 轴的正半轴,则
轴的正半轴,则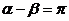 是两角终边互为反向延长线的
( A )
是两角终边互为反向延长线的
( A )
(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分也不必要条件
14、函数 ( A )
( A )
(A)在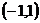 上单调递增 (B)在
上单调递增 (B)在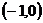 上单调递增,在
上单调递增,在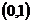 上单调递减
上单调递减
(C)在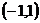 上单调递减 (D)在
上单调递减 (D)在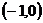 上单调递减,在
上单调递减,在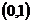 上单调递增
上单调递增
 15、2005年1月6日《文汇报》载当日我国人口达到13亿,
15、2005年1月6日《文汇报》载当日我国人口达到13亿,
如图为该报提供的我国人口统计数据。2000年第五次全国
人口普查后,专家们估算我国人口数的峰值为16亿,如果
我国的人口增长率维持在最近几年的水平,那么,我国人口
数大致在 年左右达到峰值。 ( B )
16、定义域和值域均为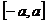 (常数
(常数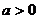 )的
)的
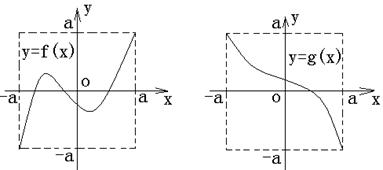 函数
函数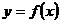 和
和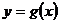 的图像如图所示,给
的图像如图所示,给
出下列四个命题:
(1)方程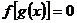 有且仅有三个解;
有且仅有三个解;
(2)方程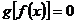 有且仅有三个解;
有且仅有三个解;
(3)方程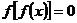 有且仅有九个解;
有且仅有九个解;
(4)方程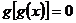 有且仅有一个解。
有且仅有一个解。
那么,其中正确命题的个数是 ( B )
(A)1 (B)2 (C)3 (D)4
三、解答题:
17、在一个圆形波浪实验水池的中心有三个振动源,假如不计其它因素,在t秒内,它们引发的水面波动可分别由函数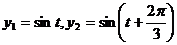 和
和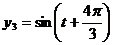 描述。如果两个振动源同时启动,则水面波动由两个函数的和表达。在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现怎样的状态,请说明理由。
描述。如果两个振动源同时启动,则水面波动由两个函数的和表达。在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现怎样的状态,请说明理由。
解:由愿意得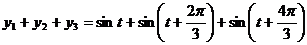
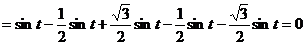
即三个振动源产生的振动被相互抵消,所以,原本平静的水面仍保持平静。
18、解关于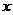 的不等式
的不等式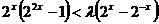
解: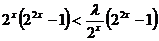 ,∵
,∵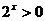 ,∴
,∴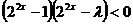
若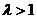 ,则
,则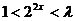 ,即
,即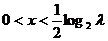 ; 若
; 若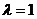 ,则
,则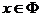 ;
;
若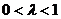 ,则
,则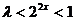 ,即
,即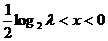 ; 若
; 若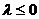 ,则
,则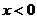 。
。
19、过直角坐标平面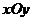 中的抛物线
中的抛物线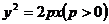 的焦点
的焦点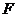 作一条倾斜角为
作一条倾斜角为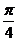 的直线与抛物线相交于A,B两点。
的直线与抛物线相交于A,B两点。
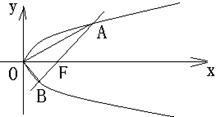 (1)用
(1)用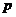 表示A,B之间的距离;
表示A,B之间的距离;
(2)证明: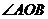 的大小是与
的大小是与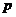 无关的定值,并求出这个值。
无关的定值,并求出这个值。
解:(1)焦点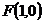 ,过抛物线的焦点且倾斜角为
,过抛物线的焦点且倾斜角为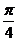 的直线方程是
的直线方程是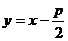
由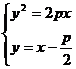
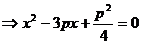
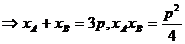
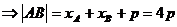
( 或 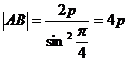 )
)
(2)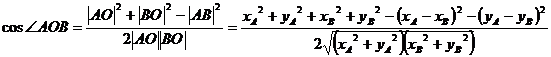
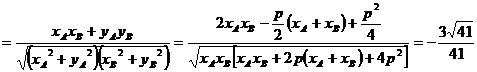
∴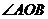 的大小是与
的大小是与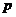 无关的定值,
无关的定值,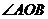
 。
。
20、一个多面体的直观图,前视图(正前方观察),俯视图(正上方观察),侧视图(左侧正前方观察)如下所示。
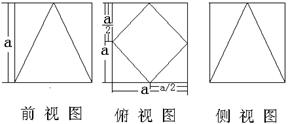
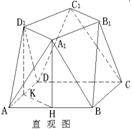 (1)求
(1)求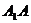 与平面
与平面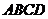 所成角的大小及
所成角的大小及
面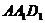 与面
与面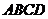 所成二面角的大小;
所成二面角的大小;
(2)求此多面体的表面积和体积。
解:(1)由已知图可得,平面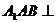 平面
平面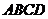 ,取
,取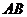 中点
中点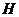 ,连接
,连接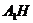 ,
,
在等腰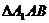 中有
中有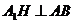 ,则
,则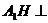 平面
平面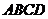 ,
,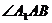 是
是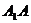 与平面
与平面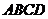 所成角,
所成角,
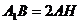 ,∴
,∴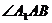
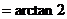
取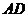 中点
中点 ,连接
,连接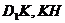 ,同理有
,同理有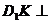 平面
平面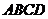 ,即
,即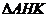 是
是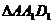 在
在
平面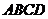 内的射影,在
内的射影,在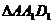 中,
中,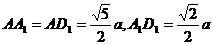 ,
,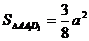
又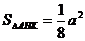 ,设面
,设面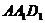 与面
与面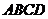 所成二面角的大小为
所成二面角的大小为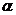 ,则
,则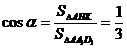
∴面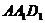 与面
与面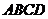 所成二面角的大小为
所成二面角的大小为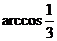 。
。
(2)此多面体的表面积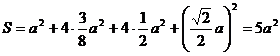
此多面体的体积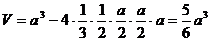
21、已知数列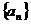 有
有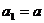 ,
,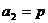 (常数
(常数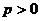 ),对任意的正整数
),对任意的正整数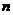 ,
,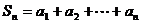 ,并有
,并有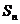 满足
满足 。
。
(1)求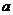 的值;
的值;
(2)试确定数列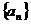 是否是等差数列,若是,求出其通项公式,若不是,说明理由;
是否是等差数列,若是,求出其通项公式,若不是,说明理由;
(3)对于数列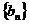 ,假如存在一个常数
,假如存在一个常数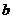 使得对任意的正整数
使得对任意的正整数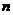 都有
都有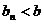 ,且
,且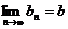 ,则称
,则称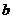 为数列
为数列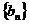 的“上渐近值”,令
的“上渐近值”,令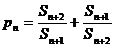 ,求数列
,求数列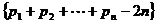 的“上渐近值”。
的“上渐近值”。
解:(1)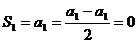 ,即
,即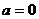
(2)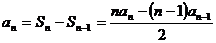
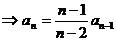
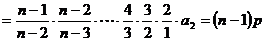
∴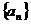 是一个以
是一个以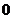 为首项,
为首项,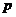 为公差的等差数列。
为公差的等差数列。
(3)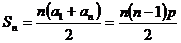 ,
,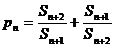
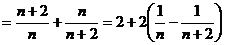
∴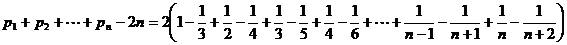
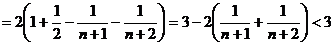
又∵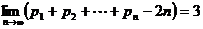 ,∴数列
,∴数列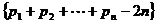 的“上渐近值”为
的“上渐近值”为 。
。
22、(1)若直角三角形两直角边长之和为12,求其周长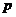 的最小值;
的最小值;
(2)若三角形有一个内角为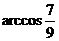 ,周长为定值
,周长为定值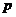 ,求面积
,求面积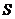 的最大值;
的最大值;
(3)为了研究边长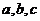 满足
满足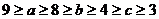 的三角形其面积是否存在最大值,现有解法如下:
的三角形其面积是否存在最大值,现有解法如下:

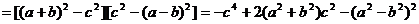
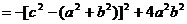
而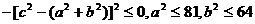 ,则
,则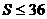 ,但是,其中等号成立的条件是
,但是,其中等号成立的条件是
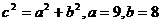 ,于是
,于是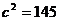 与
与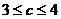 矛盾,所以,此三角形的面积不存在最大值。
矛盾,所以,此三角形的面积不存在最大值。
以上解答是否正确?若不正确,请你给出正确的答案。
(注: 称为三角形面积的海伦公式,它已经被证明是正确的)
称为三角形面积的海伦公式,它已经被证明是正确的)
解:(1)设直角三角形两直角边长为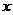 、
、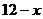 ,斜边长为
,斜边长为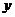 ,则
,则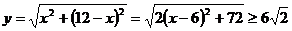
∴两直角边长为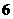 时,周长
时,周长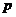 的最小值为
的最小值为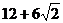 。
。
(2)设三角形中边长为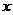 、
、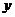 的两边所夹的角为
的两边所夹的角为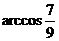 ,则周长
,则周长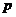
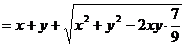
∴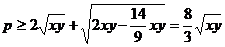 ,即
,即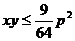
又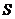
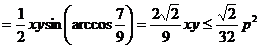 ,∴面积
,∴面积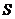 的最大值为
的最大值为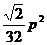 。
。
(3)不正确。
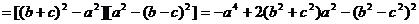
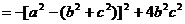
而 ,则
,则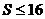 ,
,
其中等号成立的条件是
 ,则
,则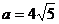
∴当三角形的边长为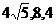 的直角三角形时,其面积取得最大值
的直角三角形时,其面积取得最大值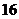 。
。
(
另法: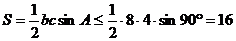 )
)