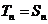1.函数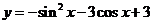 的最小值为
( )
的最小值为
( )
(A)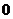 (B) 2
(C)
(B) 2
(C)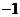 (D)
(D)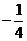
2.某单位有老年人28人,中年人54人,青年人81人,为了调查他们的身体状况,需从他们中抽取一个容量为36的样本,最适合的抽取样本的方法是 ( )
(A)简单随机抽样 (B)系统抽样
(C)分层抽样 (D)先从老年人中随机剔除1人,然后分层抽样
3.如果函数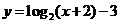 的图象按
的图象按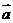 平移得到
平移得到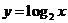 的图象,则
的图象,则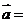 ( )
( )
(A)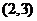 (B)
(B)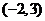 (C)
(C)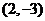 (D)
(D)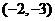
4.已知随机变量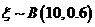 ,若
,若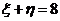 ,则
,则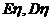 分别是 (
)
分别是 (
)
(A)6和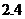 (B)2和
(B)2和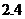 (C)2和
(C)2和 (D)6和
(D)6和
(文科)若函数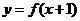 的定义域是
的定义域是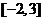 ,则
,则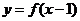 定义域是 ( )
定义域是 ( )
(A)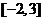 (B)
(B)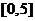 (C)
(C)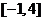 (D)
(D)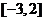
5.若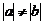 ,
,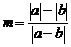 ,
,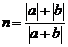 ,则
,则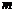 、
、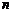 的大小关系是
(
)
的大小关系是
(
)
(A)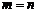 (B)
(B)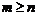 (C)
(C)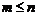 (D)无法判断
(D)无法判断
6. 函数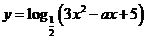 在
在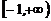 上单调递减,则
上单调递减,则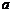 的取值范围是 ( )
的取值范围是 ( )
(A)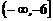 (B)
(B)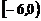 (C)
(C)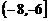 (D)
(D)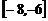
7.已知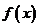 为
为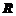 上的奇函数,且
上的奇函数,且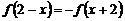 ,
,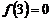 .则
.则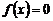 在区间
在区间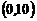 内实根的个数最少是
(
)
内实根的个数最少是
(
)
(A)10 (B)9 (C)8 (D)5
8.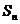 是首项为1的等比数列
是首项为1的等比数列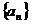 的前
的前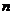 项和,若
项和,若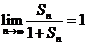 , 则公比
, 则公比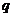 的范围是( )
的范围是( )
(A)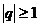 (B)
(B)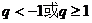 (C)
(C)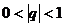 (D)
(D)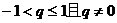
(文科)已知两个等差数列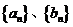 满足
满足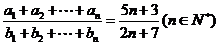 ,
,
则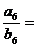 (
) (A)
(
) (A)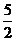 (B)
2 (C)
(B)
2 (C)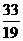 (D)
(D)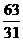
9.函数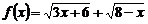 的值域是
(
)
的值域是
(
)
(A)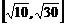 (B)
(B)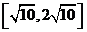 (C)
(C)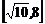 (D)
(D)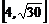
10.已知全集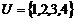 ,则满足
,则满足 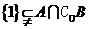 的集合对
的集合对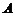 、
、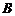 共有
(
)
共有
(
)
(A)24对 (B)27对 (C)37对 (D)42对
11.已知点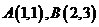 ,O为坐标原点,
,O为坐标原点,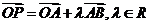 ,
若点P在第四象
,
若点P在第四象
限内,则实数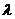 的取值范围是
.
的取值范围是
.
12.函数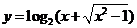 的反函数是 .
的反函数是 .
13.若集合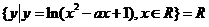 ,则实数
,则实数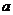 的取值范围是
.
的取值范围是
.
14. 设甲射击一次,击中目标的概率是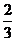 .假设每次射击是否击中目标,相互之间没有影响,且连续2次未击中目标,则停止射击.则甲恰好射击5次后,被中止射击的概率是 .
.假设每次射击是否击中目标,相互之间没有影响,且连续2次未击中目标,则停止射击.则甲恰好射击5次后,被中止射击的概率是 .
15.若关于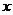 的方程
的方程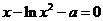 在区间
在区间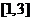 内恰有一个实根,则实数
内恰有一个实根,则实数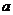 的取值范围是
.(文科)若关于
的取值范围是
.(文科)若关于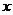 的方程
的方程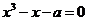 有三个不同的实根,则
有三个不同的实根,则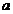 的取值范围是 .
的取值范围是 .
16.给出下列四个命题:①设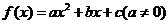 ,若
,若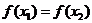
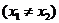 ,则
,则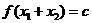 ;②若偶函数
;②若偶函数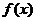 在
在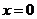 处可导,则
处可导,则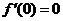 ; ③函数
; ③函数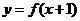 与
与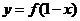 的图象关于直线
的图象关于直线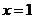 对称;④函数
对称;④函数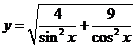 的最小值是
5.则其中错误的命题的序号是 .
的最小值是
5.则其中错误的命题的序号是 .
杭州二中高三代数质量检测题(五)答题卷
班级 姓名 学号
(11)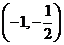 ,(12)
,(12) 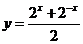 ,
,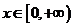 ,(13)
,(13)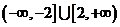 ,
,
(14)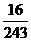 ,(15)
,(15)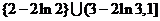 ,文
,文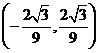 (16)③
(16)③
17.已知向量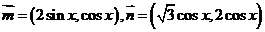 ,定义函数
,定义函数
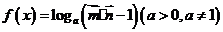 ,求函数
,求函数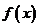 的最小正周期、单调递增区间.
的最小正周期、单调递增区间.
解:.因为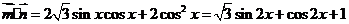
所以 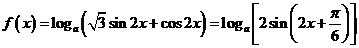 ,故
,故  ,
,
令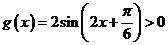 ,则
,则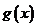 的单调递增的正值区间是
的单调递增的正值区间是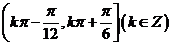 ,单调递减的正值区间是
,单调递减的正值区间是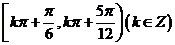 则当
则当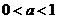 时,函数
时,函数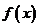 的单调递增区间为
的单调递增区间为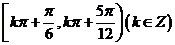
当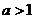 时,函数
时,函数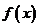 的单调递增区间为
的单调递增区间为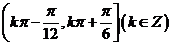
18.已知不等式 对任意
对任意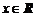 恒成立,试求实数a的取值范围.
恒成立,试求实数a的取值范围.
解:令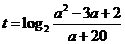 ,则
,则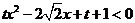 对任意
对任意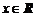 恒成立
恒成立
则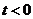 ,且
,且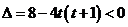 ,解得:
,解得: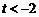
所以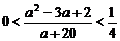 ,解得
,解得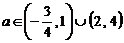 ,
,
19.已知f(x)=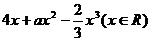 在区间[-1,1]上是增函数.(1)求实数a的值组成的集合A;(2)设关于x的方程f(x)=
在区间[-1,1]上是增函数.(1)求实数a的值组成的集合A;(2)设关于x的方程f(x)= 的两个非零实根为x1、x2.是否存在实数m,使得对任意a∈A及t∈[-1,1],不等式m2+tm+1≥|x1-x2|恒成立?
的两个非零实根为x1、x2.是否存在实数m,使得对任意a∈A及t∈[-1,1],不等式m2+tm+1≥|x1-x2|恒成立?
解:(2004福建文T22)
(1)f'(x)=4+2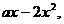 ∵f(x)在[-1,1]上是增函数,∴f'(x)≥0对x∈[-1,1]恒成立,即x2-ax-2≤0对x∈[-1,1]恒成立.
①
设
∵f(x)在[-1,1]上是增函数,∴f'(x)≥0对x∈[-1,1]恒成立,即x2-ax-2≤0对x∈[-1,1]恒成立.
①
设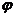 (x)=x2-ax-2,
(x)=x2-ax-2,
方法一:
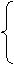
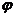 (1)=1-a-2≤0,
(1)=1-a-2≤0,
①
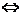
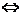 -1≤a≤1,
-1≤a≤1,
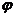 (-1)=1+a-2≤0.∵对x∈[-1,1],只有当a=1时,f'(-1)=0以及当a=-1时,f'(1)=0∴A={a|-1≤a≤1}.
(-1)=1+a-2≤0.∵对x∈[-1,1],只有当a=1时,f'(-1)=0以及当a=-1时,f'(1)=0∴A={a|-1≤a≤1}.
方法二:
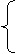
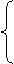
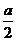 ≥0,
≥0,
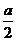 <0,
<0,
① 或
或
 (-1)=1+a-2≤0
(-1)=1+a-2≤0 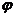 (1)=1-a-2≤0
(1)=1-a-2≤0
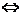 0≤a≤1 或 -1≤a≤0
0≤a≤1 或 -1≤a≤0 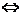 -1≤a≤1.
-1≤a≤1.
∵对x∈[-1,1],只有当a=1时,f'(-1)=0以及当a=-1时,f'(1)=0
∴A={a|-1≤a≤1}.
(2)由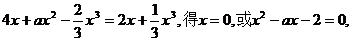
∵△=a2+8>0∴x1,x2是方程x2-ax-2=0的两非零实根,
x1+x2=a,x1x2=-2 从而|x1-x2|=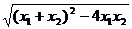 =
=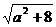 ,
,
∵-1≤a≤1,∴|x1-x2|=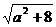 ≤3.
≤3.
要使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,
当且仅当m2+tm+1≥3即m2+tm-2≥0对任意t∈[-1,1]恒成立. ②
设g(t)=m2+tm-2=mt+(m2-2),
方法一:
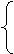 g(-1)=m2-m-2≥0,
g(-1)=m2-m-2≥0,
② 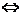
g(1)=m2+m-2≥0,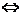 m≥2或m≤-2.
m≥2或m≤-2.
方法二:当m=0时,②显然不成立;当m≠0时,
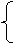
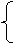 m>0,
m<0,
m>0,
m<0,
②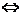 或
或
g(-1)=m2-m-2≥0 g(1)=m2+m-2≥0
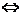 m≥2或m≤-2.
m≥2或m≤-2.
所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.
20.已知数列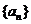 满足:
满足: ,且
,且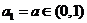 .
.
(1)用数学归纳法证明: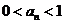 ;(2)试求
;(2)试求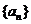 的通项公式;(3)对于
的通项公式;(3)对于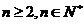 ,求证:
,求证: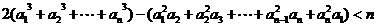 .
.
提示:(2)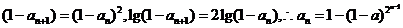
(3)分析:由已知可得: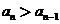
方法1: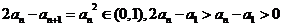 ,所以左边=
,所以左边=
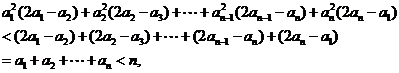
方法2: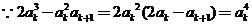
故:左边=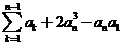
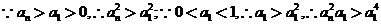
故:左边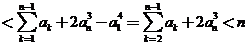
方法3:由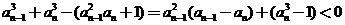
又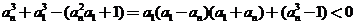
累加可证
方法4:对上面方法3的一种推广:
对任意的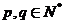 ,
,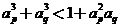
证明如下:若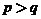 ,
,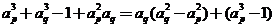
 ,
,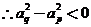 ,故得证
,故得证
若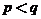 ,则
,则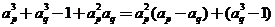
同理可证
这样,利用上述命题,对左边各式进行任意组合,便可证明
(文科)设等比数列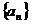 的公比为
的公比为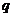 ,前n项和
,前n项和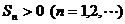 .(1)求
.(1)求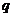 的取值范围;(2)设
的取值范围;(2)设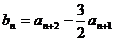 ,记
,记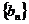 的前n项和为
的前n项和为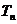 ,试比较
,试比较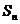 与
与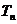 的大小.
的大小.
解:(2005全国卷Ⅰ)
(1)因为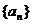 是等比数列,
是等比数列,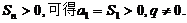 当
当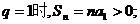
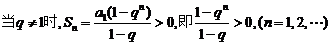
上式等价于不等式组: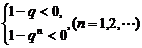 ①
①
或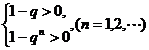 ②
②
解①式得q>1;解②,由于n可为奇数、可为偶数,得-1<q<1.
综上,q的取值范围是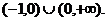
(2)由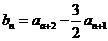 得
得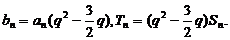
于是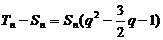
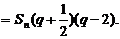
又∵ >0且-1<
>0且-1<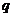 <0或
<0或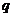 >0
>0
当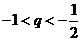 或
或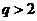 时
时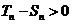 即
即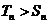
当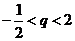 且
且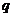 ≠0时,
≠0时,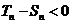 即
即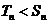
当 或
或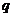 =2时,
=2时,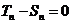 即
即