
(1)(理)复数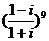 的虚部是
( )
的虚部是
( )
(A) (B)
(B)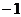 (C)
(C)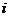 (D)
(D)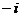
(文)设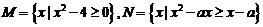 ,若
,若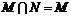 ,则
,则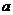 的取值范围
的取值范围
是 ( )
(A)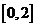 (B)
(B)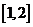 (C)
(C)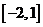 (D)
(D)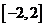
(2)已知向量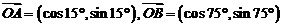 ,则
,则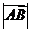 为 ( )
为 ( )
(A)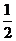 (B)
(B)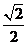 (C)
(C)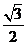 (D)1
(D)1
(3)等比数列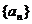 中,
中,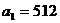 ,公比
,公比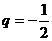 ,用
,用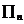 表示它的前
表示它的前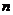 项之积:
项之积: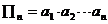 ,则
,则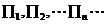 中最大的是
( )
中最大的是
( )
(A)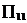 (B)
(B)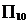 (C)
(C) 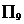 (D)
(D)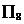
(4)在△ABC中,面积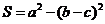 ,则
,则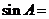 ( )
( )
(A)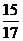 (B)
(B)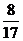 (C)
(C)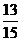 (D)
(D)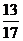
 (5)如图所示的电路,有
(5)如图所示的电路,有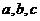 三个开关,每个开关开或关
三个开关,每个开关开或关
的概率都是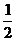 ,且是相互独立的,则灯泡甲亮的概率为
,且是相互独立的,则灯泡甲亮的概率为
(A)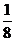 (B)
(B)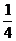 (C)
(C)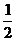 (D)
(D)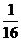
(6)随机变量ξ的概率分布规律为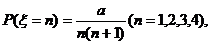 其中a是常数,则
其中a是常数,则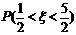 的值为
( )
的值为
( )
(A)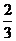 (B)
(B)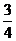 (C)
(C)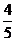 (D)
(D)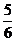
(7)设函数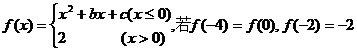 ,则关于x的方程
,则关于x的方程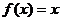 的解的个数为 ( )
的解的个数为 ( )
(A)1个 (B)2个 (C)3个 (D)4个
(8)(理)若logbπ<logaπ<0,
则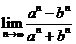 =
(
)
=
(
)
(A)1 (B) -1 (C) 0 (D)3
(文)已知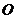 为原点,
为原点,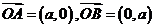 其中
其中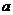 为常数且
为常数且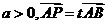
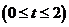 ,则
,则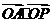 的最小值是
(
)
的最小值是
(
)
(A)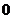 (B)
(B)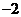 (C)
(C)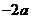 (D)
(D)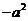
(9)按一次电视机遥控器上的电源开关,电视机可能出现以下三种情况:①由原来的关机状态转为开机状态;②由原来的开机状态转为关机状态;③电视机保持原来的状态不变.由于电视机从关机状态转为开机状态要等待一段时间,一台电视机处于关机状态时,某人连续按了4次电源开关,结果使电视转为开机,则他所按的4次中可以发生的所有的情况种数为 ( )
(A)8 (B)12 (C)16 (D)20
(10)实系数方程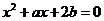 的一根大于0且小于1,另一个根大于1且小于2,则
的一根大于0且小于1,另一个根大于1且小于2,则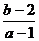 的取值范围是
( )
的取值范围是
( )
(A)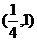 (B)
(B)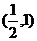 (C)
(C)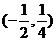 (D)
(D)
(11)某厂包装车间对包装质量进行检查时,采用这样的方法:在自动包装传送带上,每隔30分钟抽一包产品,进行质量检查,这样的抽样方法是 抽样.
(12)梯形的两对角线把梯形分成四部分, 有五种不同的颜色给这四部分涂色, 每一部分
涂一种颜色, 任何相邻(具有公共边)的两部分涂不同的颜色, 则不同的涂色方法有 种.
(13)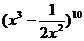 展开式中的常数项为
.
展开式中的常数项为
.
(14)函数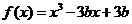 在(0,1)内有极小值,则实数
在(0,1)内有极小值,则实数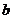 的取值范围是____ ____.
的取值范围是____ ____.
杭州二中高三代数综合测试四答题卷
班级 姓名 学号
(11) (12) (13) (14)
(15)近日国内某大报纸有如下报导:
|
加薪的学问 学数学,其实是要使人聪明,使人的思维更加缜密.在美国广为流传的一道数学题目:老板给出两个加工资的方案,一是每年年末加一千;二是每半年结束时加300元,请选一种.一般不擅长数学的,很容易选前者,因为一年加一千元总比两半年共600元要多.其实,由于加工资是累计的,时间稍长,往往第二种方案更有利.例如,在二年的年末,依第一种方案可以加得1000+2000=3000元,而第二种方案在第一年加得300+600元,第二年加得900+1200=2100元,总数也是3000元.但到第三年,第一方案可得1000+2000+3000=6000元,第二种方案则为300+600+900+1200+1500+1800=6300元,比第一方案多了300元.第四年、第五年会更多.因此,你若会在该公司工作三年以上,则应选择第二方案. |
根据以上材料,解答下列问题: (Ⅰ)如果在该公司干10年,问选择第二方案比选择第一方案多加薪水多少元? (Ⅱ)如果第二方案中的每半年加300元改成每半年加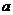 元,问
元,问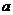 取何值时,总是选择第二方案比选择第一方案多加薪?
取何值时,总是选择第二方案比选择第一方案多加薪?
(16)已知函数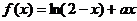 在
在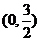 上是增函数,
上是增函数,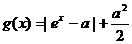 .当
.当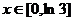 时,函数
时,函数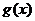 的最大值
的最大值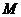 与
与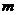 最小值的差为
最小值的差为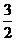 ,试求
,试求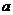 的值.
的值.
(17)(理)盒子中有大小相同的球10个,其中标号为1的球3个,标号为2的球4个,标号为5的球3个,第一次从盒中任意取1个球,放回后第二次再任意取一个球(假设取到每个球的可能性都相同),记第一次与第二次取到球的标号之和为 .
.
(Ⅰ)求随机变量 的分布列; (Ⅱ)求
的分布列; (Ⅱ)求 的数学期望.
的数学期望.
(文)从4名男生和2名女生中任选3人参加演讲比赛,
(Ⅰ)求所选3人都是男生的概率; (Ⅱ)求所选3人中恰有1名女生的概率;
(Ⅲ)求所选3人中至少有一名女生的概率.
(18)已知点集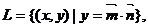 其中
其中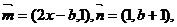 点列
点列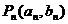 在
在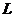 中,
中,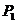 为
为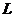 与
与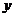 轴的交点,等差数列
轴的交点,等差数列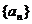 的公差为1,
的公差为1,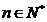 .
.
(Ⅰ)求数列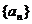 ,
,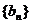 的通项公式; (Ⅱ)(理)若
的通项公式; (Ⅱ)(理)若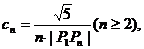 求
求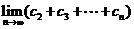 ; (Ⅲ)若
; (Ⅲ)若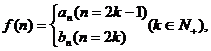 是否存在
是否存在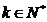 使得
使得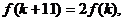 若存在,求出
若存在,求出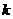 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
杭州二中高三代数综合测试四(2005-12-19) (下午3:05-4:35)参考答案
代数综合测试四参考答案仅供参考)
B/DDCBA、DCB/DAA, 系统抽样、260、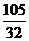 、
、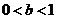
15、解:(Ⅰ)在该公司干10年,第一种方案多加的薪水为:
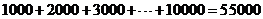
第二种方案多加的薪水为:
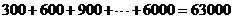
(Ⅱ)设在该公司工作时间为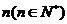 年,则
年,则
第一方案多加的薪水为: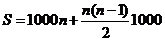 ;
;
第二方案多加的薪水为: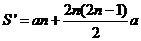 ;
;
即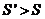 对
对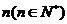 恒成立,得:
恒成立,得: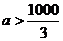 .
.
16、解:解: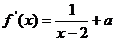 ,
,
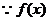 在
在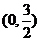 上是增函数.
上是增函数.
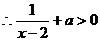 在
在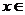
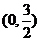 上恒成立,
上恒成立,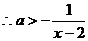 恒成立,
恒成立,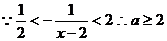 .
.
设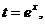 则
则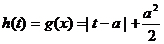 ,
,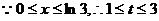
(ⅰ)当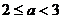 时,
时,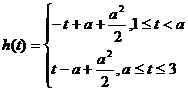
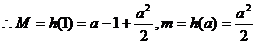 ,
,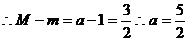
(ⅱ)当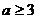 时,
时,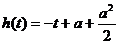
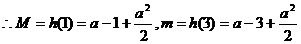 ,
,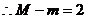 不符题意.
不符题意.
综上,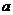 的取值为
的取值为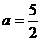 . (对于不同的解法可根据本解法酌情给分)
. (对于不同的解法可根据本解法酌情给分)
17、(理)解:(Ⅰ)
 |
2 |
3 |
4 |
6 |
7 |
10 |
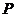 |
0.09 |
0.24 |
0.16 |
0.18 |
0.24 |
0.09 |
(Ⅱ)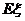 =5.2
=5.2
(文)解:(Ⅰ)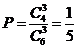 ;(Ⅱ)
;(Ⅱ)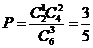 ;(Ⅲ)
;(Ⅲ)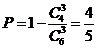 .
.
18、解:(1)由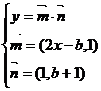 ,得
,得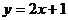
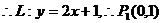 ,则
,则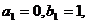
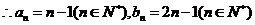
(2)当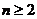 时,,
时,,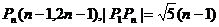
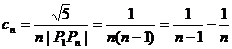 ,
, 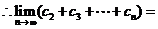
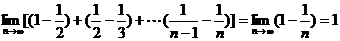
(3)假设存在符合条件的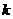 使命题成立
使命题成立
当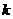 是偶数时,
是偶数时,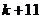 是奇数,则
是奇数,则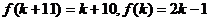
由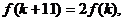 得
得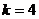 ;
;
当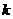 是奇数时,
是奇数时,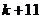 是偶数,则
是偶数,则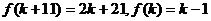 ,
,
由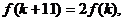 得
得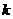 无解,综上存在
无解,综上存在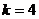 ,使得
,使得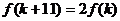 .
.
(对于不同的解法可根据本解法酌情给分)