
一项是符合题目要求的.
1.下列函数中,周期为1的奇函数是 ( )
A.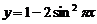 B.
B.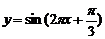 C.
C.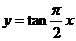 D.
D.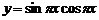
2.ω是正实数,函数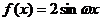 在
在 上是增函数,那么 ( )
上是增函数,那么 ( )
A.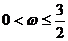 B.
B.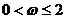 C.
C.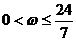 D.
D.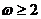
3.对于函数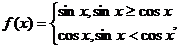 则下列正确的是 ( )
则下列正确的是 ( )
A.该函数的值域是[-1,1]
B.当且仅当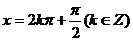 时,该函数取得最大值1
时,该函数取得最大值1
C.当且仅当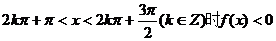
D.该函数是以π为最小正周期的周期函数
4.若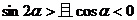 ,则α是 ( )
,则α是 ( )
A.第二象限角 B.第三象限角
C.第一或第三象限角 D.第二或第三象限角
5.函数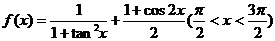 的值域是 ( )
的值域是 ( )
A.[-2,2] B.(0,2) C.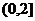 D.
D.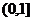
6.函数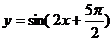 的图象的一条对称轴方程是 ( )
的图象的一条对称轴方程是 ( )
A.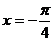 B.
B.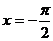 C.
C.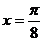 D.
D.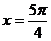
7.函数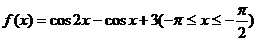 有 ( )
有 ( )
A.最大值3,最小值2 B.最大值5,最小值3
C.最大值5,最小值2 D.最大值3,最小值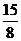
8.若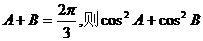 的值的范围是 ( )
的值的范围是 ( )
A.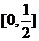 B.
B.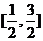 C.
C.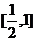 D.[0,1]
D.[0,1]
9.要使函数 在区间[
在区间[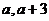 ]
]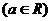 上出现的次数不少于4次,不多于8次,则k的值是 ( )
上出现的次数不少于4次,不多于8次,则k的值是 ( )
A.2 B.3 C.4或5 D.2或3
10.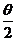 是第四象限角,
是第四象限角,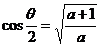 则
则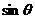 的值是 ( )
的值是 ( )
A.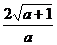 B.
B.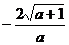 C.
C.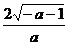 D.
D.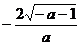
11.函数f(x)=|sinx+cosx|-|sinx-cosx|是 ( )
A.最小正周期为2π的奇函数 B.最小正周期为2π的偶函数
C.最小正周期为π的奇函数 D.最小正周期为π的偶函数
12.将函数y=sin(2x+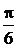 )(x∈R)的图象上所有点向右平移
)(x∈R)的图象上所有点向右平移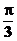 个单位(纵坐标不变),则所得到
个单位(纵坐标不变),则所得到
的图象的解析式是 ( )
A.y=-cos2x B.y=cos2x C.y=sin(2x+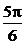 ) D.y=sin(2x-
) D.y=sin(2x-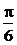 )
)
13.函数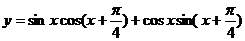 的最小正周期T=
。
的最小正周期T=
。
14.若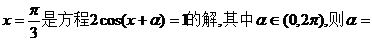 .
.
15.计算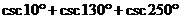 ,所得数值等于
_。
,所得数值等于
_。
16.函数y=sin2x+2cosx在区间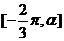 上的最小值为
上的最小值为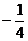 ,则
,则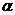 的取值范围是
。
的取值范围是
。
17.(本小题满分12分)已知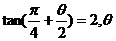 为锐角,求
为锐角,求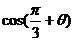 的值。
的值。
18.(本小题满分12分)已知函数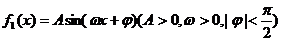 的部分图象如图所示:
的部分图象如图所示:
⑴求此函数的解析式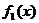 ;
;
 ⑵与
⑵与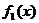 的图象关于x=8对称的函数解析式
的图象关于x=8对称的函数解析式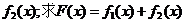 单增区间.
单增区间.
19.(本小题满分12分)设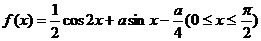
⑴用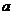 表示
表示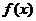 的最大值
的最大值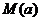 ;
;
⑵当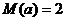 时,求
时,求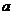 的值。
的值。
20.(本小题满分12分) 已知函数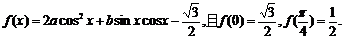
⑴求f(x)的最小正周期;
⑵求f(x)的单调递减区间;
⑶函数f(x)的图象经过怎样的平移才能使其对应的函数成为奇函数?
21.(本小题满分12分)已知△ABC中,∠A、∠B、∠C的对边分别是a、b、c,若
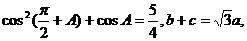 求A、B、C的大小。
求A、B、C的大小。
22.(本小题满分14分)
设a,b为常数,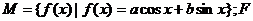 :把平面上任意一点(a,b)映射为函数
:把平面上任意一点(a,b)映射为函数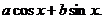
(1)证明:不存在两个不同点对应于同一个函数;
(2)证明:当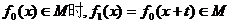 ,这里t为常数;
,这里t为常数;
(3)对于属于M的一个固定值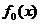 ,得
,得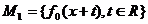 ,在映射F的作用下,M1作为象,求其原象,并说明它是什么图象.
,在映射F的作用下,M1作为象,求其原象,并说明它是什么图象.
高三单元试题之四三角函数 (时量:120分钟 满分:150分)参考答案
高三单元试题之四:三角函数参考答案
一、1.D 2.A 3.C 4.B 5.C 6.B 7.C 8.B 9.D 10.C 11.C 12.A
二、13.p 14. 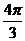 15. 6 16.
15. 6 16.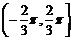
三、17. ,
,
又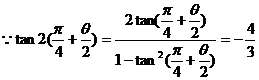 ,
∴tan
,
∴tan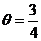 。
。
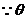 为锐角 ∴sin
为锐角 ∴sin 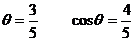 ,
,
∴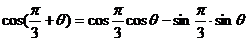
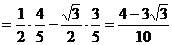 .
.
18.⑴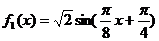 。
。
⑵设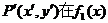 上,则P′点关于x=8对称点
上,则P′点关于x=8对称点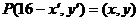
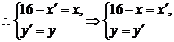
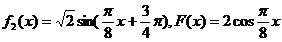 ,
,
单增区间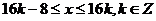 。
。
19.解:⑴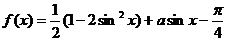
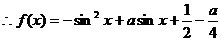

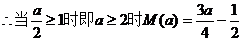
当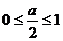 即
即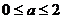 时
时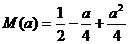
当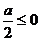 即
即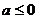 时
时
⑵当 时
,
时
,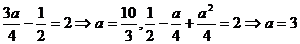 或
或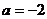 (舍)
(舍) 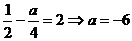
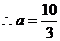 或
或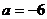
20.⑴由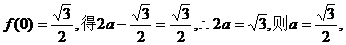
由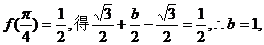
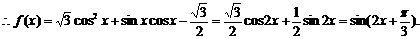
∴函数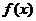 的最小正周期T=
的最小正周期T=
⑵由
∴f(x)的单调递减区间是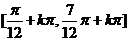
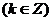 .
.
⑶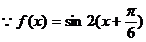 ,∴奇函数
,∴奇函数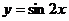 的图象左移
的图象左移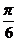 即得到
即得到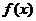 的图象,
的图象,
故函数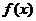 的图象右移
的图象右移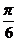 后对应的函数成为奇函数.
后对应的函数成为奇函数.
(注:第⑶问答案不唯一,教师阅卷时可灵活处理.)
21.解:由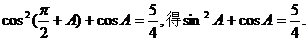
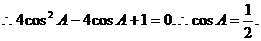
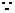 A是△ABC的内角,
A是△ABC的内角,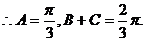
由正弦定理知sinB+sinC=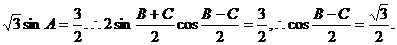
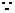 B、C是△ABC的内角,
B、C是△ABC的内角,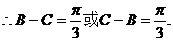
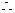 B=
B=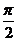 ,C=
,C=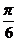 或C=
或C=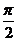 ,B=
,B=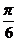 .
.
22.⑴假设有两个不同的点(a,b),(c,d)对应同一函数,即 与
与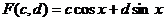 相同,即
相同,即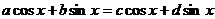 为一切实数x成立.
为一切实数x成立.
令x=0,得a=c;令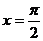 ,得b=d这与(a,b),(c,d)是两个不同点矛盾,假设不成立.
,得b=d这与(a,b),(c,d)是两个不同点矛盾,假设不成立.
故不存在两个不同点对应同函数。
⑵当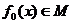 时,可得常数a0,b0,使
时,可得常数a0,b0,使 =
=
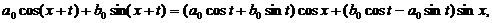
因为 为常数,设
为常数,设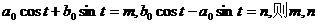 是常数.
是常数.
所以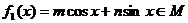 。
。
⑶设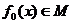 ,由此得
,由此得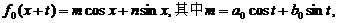
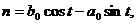 在映射F之下,
在映射F之下,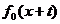 的原象是(m,n),则M1的原象是
的原象是(m,n),则M1的原象是
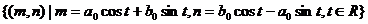 .
.
消去t得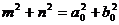 ,即在映射F之下,M1的原象
,即在映射F之下,M1的原象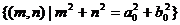 是以原点为圆心,
是以原点为圆心,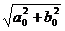 为半径的圆.
为半径的圆.