
具有斜率的弦中点问题,一般设曲线上两点为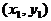 ,
,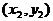 ,代入方程,然后两方程相减,再应用中点关系及斜率公式,消去四个参数。
,代入方程,然后两方程相减,再应用中点关系及斜率公式,消去四个参数。
例1 给定双曲线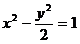 。过A(2,1)的直线与双曲线交于两点
。过A(2,1)的直线与双曲线交于两点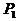 及
及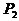 ,求线段
,求线段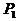
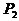 的中点P的轨迹方程。
的中点P的轨迹方程。
分析:设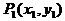 ,
,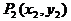 代入方程得
代入方程得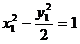 ,
,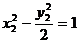 。
。
两式相减得
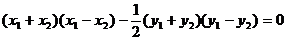 。
。
又设中点P(x,y),将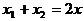 ,
,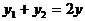 代入,当
代入,当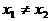 时得
时得
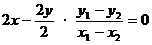 。
。
又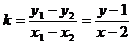 ,
,
代入得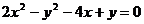 。
。
当弦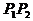 斜率不存在时,其中点P(2,0)的坐标也满足上述方程。因此所求轨迹方程是
斜率不存在时,其中点P(2,0)的坐标也满足上述方程。因此所求轨迹方程是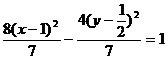 。
。
例2 已知椭圆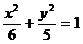 ,通过点(1,1)引一弦,使它在这点被平分,求此弦所在的直线方程。
,通过点(1,1)引一弦,使它在这点被平分,求此弦所在的直线方程。
略解:有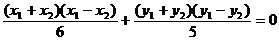 ,代入得
,代入得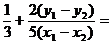
0,得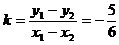 。
。
从而直线方程是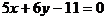 。
。
此题将椭圆变为双曲线、抛物线都是同一方法。
椭圆或双曲线上一点P,与两个焦点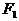 、
、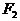 构成的三角形问题,常用正、余弦定理搭桥。
构成的三角形问题,常用正、余弦定理搭桥。
例3 设P(x,y)为椭圆 上任一点,
上任一点,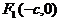 ,
,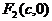 为焦点,
为焦点,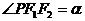 ,
,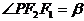 。
。
(1)求证离心率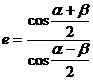 ;
;
(2)求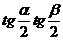 的值;
的值;
(3)求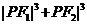 的最值。
的最值。
分析:(1)设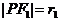 ,
,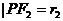 ,由正弦定理得
,由正弦定理得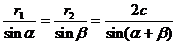 。
。
得 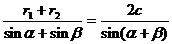 ,
,
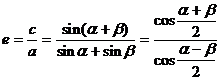 。
。
(2)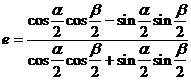 ,采用合分比定理得
,采用合分比定理得
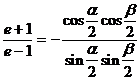 ,
,
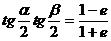 。
。
(3)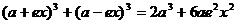 。
。
当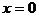 时,最小值是
时,最小值是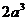 ;
;
当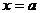 时,最大值是
时,最大值是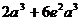 。
。
在曲线上两点关于某直线对称问题,分三步:求两点所在的直线,求这两直线的交点,使这交点在圆锥曲线形内。
例4 已知椭圆C的方程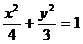 ,试确定m的取值范围,使得对于直线
,试确定m的取值范围,使得对于直线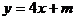 ,椭圆C上有不同两点关于直线对称。
,椭圆C上有不同两点关于直线对称。
分析:椭圆上两点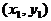 ,
,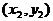 ,代入方程,相减得
,代入方程,相减得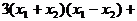
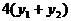
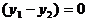 。
。
又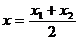 ,
,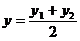 ,
,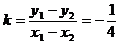 ,代入得
,代入得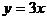 。
。
又由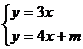 解得交点
解得交点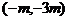 。
。
交点在椭圆内,则有
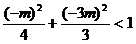 。
。
得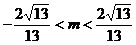 。
。
例5 为了使抛物线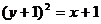 上存在两点关于直线
上存在两点关于直线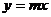 对称,求m的取值范围。
对称,求m的取值范围。
略解:两点所在直线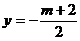 与
与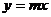 联立求出交点
联立求出交点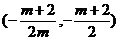 ,代入抛物线内,有
,代入抛物线内,有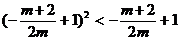 ,解得
,解得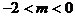 。
。
圆锥曲线两焦半径互相垂直问题,常用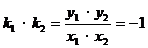 来处理。
来处理。
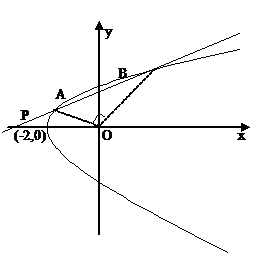
例6 已知直线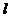 的斜率为
的斜率为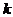 ,且过点
,且过点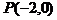 ,抛物线
,抛物线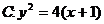 ,直线
,直线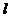 与抛物线C有两个不同的交点(如图)。
与抛物线C有两个不同的交点(如图)。
(1)求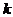 的取值范围;
的取值范围;
(2)直线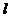 的倾斜角
的倾斜角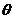 为何值时,A、B与抛物线C的焦点连线互相垂直。
为何值时,A、B与抛物线C的焦点连线互相垂直。
分析:(1)直线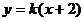 代入抛物线方程得
代入抛物线方程得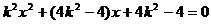 ,
,
由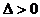 ,得
,得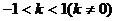 。
。
(2)由上面方程得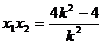 ,
,
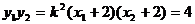 ,焦点为
,焦点为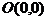 。
。
由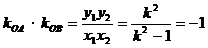 ,得
,得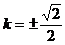 ,
,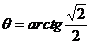 或
或
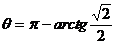 。
。
例7 经过坐标原点的直线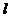 与椭圆
与椭圆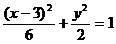 相交于A、B两点,若以AB为直径的圆恰好通过椭圆左焦点F,求直线
相交于A、B两点,若以AB为直径的圆恰好通过椭圆左焦点F,求直线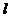 的倾斜角。
的倾斜角。
分析:左焦点F(1,0), 直线y=kx代入椭圆得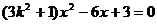 ,
,
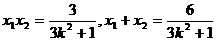 ,
,
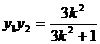 。
。
由AF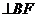 知
知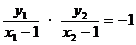 。将上述三式代入得
。将上述三式代入得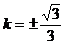 ,
,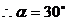 或
或 。
。
基本知识点:
(1)求解直线与圆锥曲线的位置关系的基本方法是解方程组,进而转化为一元二次方程后利用判别式,应特别注意数形结合的办法。
(2)注意韦达定理的应用。
弦长公式:斜率为k的直线被圆锥曲线截得弦AB,若A、B两点的坐标分别是A(x1,y1),B(x2,y2)则
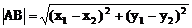
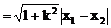

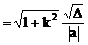
(3)注意斜率不存在的情况的讨论和焦半径公式的使用。
(4)有关中点弦问题
<1>已知直线与圆锥曲线方程,求弦的中点及与中点有关的问题,常用韦达定理。
<2>有关弦的中点轨迹,中点弦所在直线方程,中点坐标问题,有时采用“差分法”可简化运算。
(5)有关圆锥曲线的对称问题
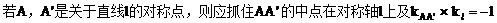
这两个关键条件,同时要记住一些特殊的对称关系,如关于坐标轴对称,关于点对称,关于直线y=±x+b对称。
(6)圆锥曲线中的有关最值问题,常用代数法和几何法解决。
<1>若命题的条件和结论具有明显的几何意义,一般可用图形性质来解决。
<2>若命题的条件和结论体现明确的函数关系式,则可建立目标函数(通常利用二次函数,三角函数,均值不等式)求最值。
[例题选讲]
例1. 已知抛物线y2=2px(p>0)。过动点M(a,0)且斜率为l的直线l与该抛物线交于不同的两点A、B
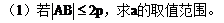
(2)若线段AB的垂直平分线交AB于Q,交x轴于点N,试求三角形MNQ的面积。
解: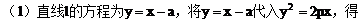
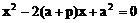
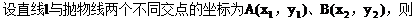
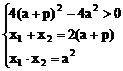
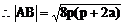
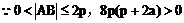
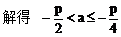
(2)设Q(x3,y3)由中点坐标公式得
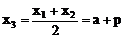
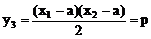
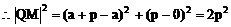
又三角形MNQ为等腰直角三角形
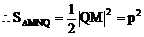
例2. 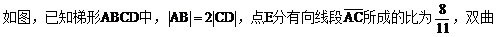 线过C、D、E三点,且以A、B为焦点,求双曲线的离心率。(2000年,全国高考)
线过C、D、E三点,且以A、B为焦点,求双曲线的离心率。(2000年,全国高考)
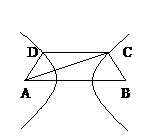
解:以AB的垂直平分线为y轴,直线AB为x轴,建立直角坐标系xOy,则CD⊥y轴,因为双曲线经过点C、D,且以A、B为焦点,由双曲线的对称性知C、D关于y轴对称。
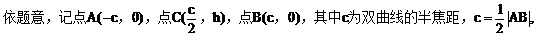
h是梯形的高。
由定比分点坐标公式,得点E的坐标为
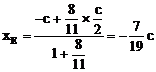
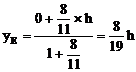

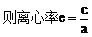
由点C、E在双曲线上,得
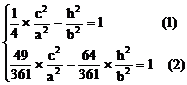
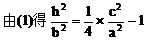
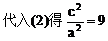
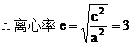
小结:此题涉及解析几何的最根本问题:如何建立坐标系,这也是对学生基本能力的考查,坐标系是一种工具,如果用得好,可以给解题带来方便,但考试时我们不可能对各种情况进行讨论,一般而言,可从对称的角度去考虑。
例3. 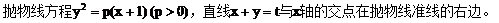
(1)求证:直线与抛物线总有两个不同交点
(2)设直线与抛物线的交点为A、B,且OA⊥OB,求p关于t的函数f(t)的表达式。
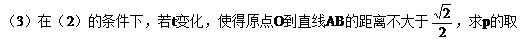 值范围。(1997年.上海高考)
值范围。(1997年.上海高考)
(1)证明:抛物线的准线为
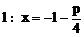
由直线x+y=t与x轴的交点(t,0)在准线右边,得
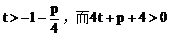
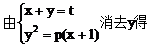
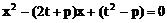
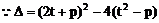
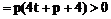
故直线与抛物线总有两个交点。
(2)解:设点A(x1,y1),点B(x2,y2)
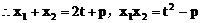
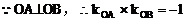
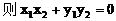
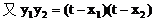
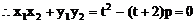
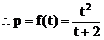
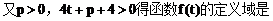
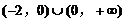
(3)解: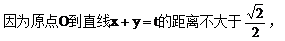
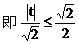
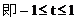
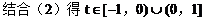
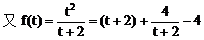
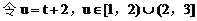
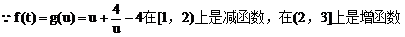
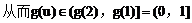
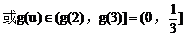
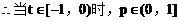
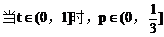
例4. 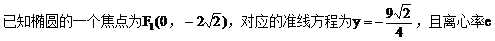

(1)求椭圆方程;
(2)是否存在直线l,使l与椭圆交于不同的两点M、N,且线段MN恰被直线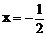 平分,若存在,求出l的倾斜角的范围;若不存在,请说明理由。
平分,若存在,求出l的倾斜角的范围;若不存在,请说明理由。
(1)解: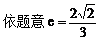
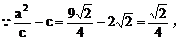
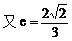
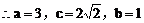
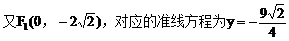

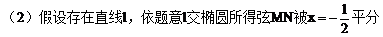
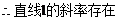
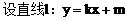
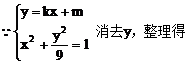

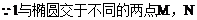
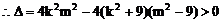
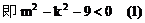
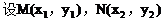
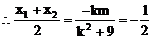
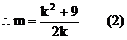
把(2)代入(1)式中得:
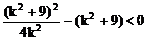
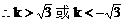
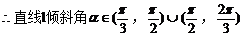
例5. 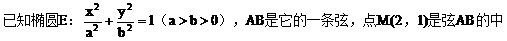 点,若以M(2,1)为焦点,椭圆E的右准线为相应准线的双曲线C和直线AB交于点N(4,-1),且椭圆的离心率e与双曲线离心率e1之间满足ee1=1,
点,若以M(2,1)为焦点,椭圆E的右准线为相应准线的双曲线C和直线AB交于点N(4,-1),且椭圆的离心率e与双曲线离心率e1之间满足ee1=1,
(1)求椭圆E的离心率e;
(2)求双曲线C的方程。
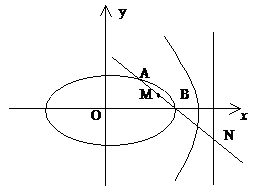
解:(1)因为点M(2,1),点N(4,-1)
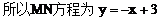
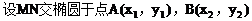
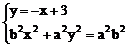
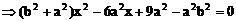
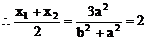
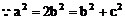
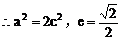
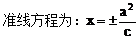
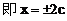
(2)因为ee1=1
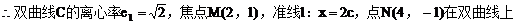
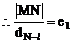
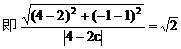
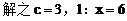
设双曲线C上一点P(x,y)
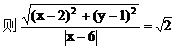
化简得双曲线C的方程:
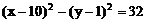
例6. 已知抛物线y2=x上有一条长为l的动弦AB,求AB的中点M到y轴的最短距离。
解:设中点M的坐标为(x,y),利用对称性可设A(x+u,y+v),B(x-u,y-v),依题意有
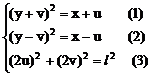
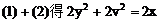
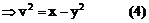

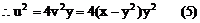
将(4)(5)代入(3)得:
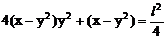
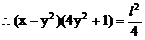
此即M点的方程
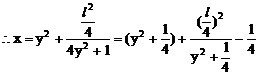
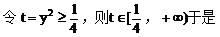
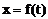
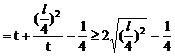
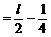
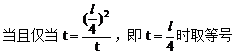

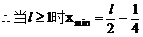
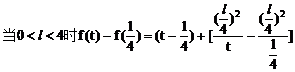
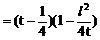
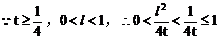
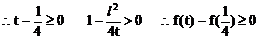

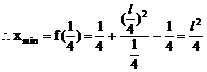
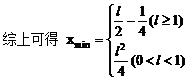
在教学中,学生普遍觉得解析几何问题的计算量较大。事实上,如果我们能够充分利用几何图形、韦达定理、曲线系方程,以及运用“设而不求”的策略,往往能够减少计算量。下面举例说明。
解析几何的研究对象就是几何图形及其性质,所以在处理解析几何问题时,除了运用代数方程外,充分挖掘几何条件,并结合平面几何知识,这往往能减少计算量。
例1. 已知直线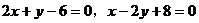 及
及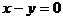 ,求它们所围成的三角形的外接圆方程。
,求它们所围成的三角形的外接圆方程。
解:由直线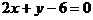 与
与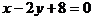 的斜率分别为
的斜率分别为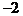 和
和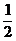 ,得此两条直线互相垂直,即此三角形为直角三角形。
,得此两条直线互相垂直,即此三角形为直角三角形。
由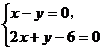 及
及 ,可求得直角三角形的斜边所在的两个顶点分别为
,可求得直角三角形的斜边所在的两个顶点分别为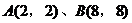 。所求三角形的外接圆,即为以A(2,2)和B(8,8)为直径端点的圆,其方程为
。所求三角形的外接圆,即为以A(2,2)和B(8,8)为直径端点的圆,其方程为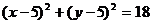
评注:此题若不首先利用三角形是直角三角形这一中间结论,而先求三角形的三个顶点,再解三元一次方程组求圆的一般方程,将会大大增加计算量。
例2. 已知点P(5,0)和圆O: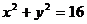 ,过P作直线
,过P作直线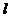 与圆O交于A、B两点,求弦AB中点M的轨迹方程。
与圆O交于A、B两点,求弦AB中点M的轨迹方程。
解: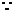 点M是弦AB中点,
点M是弦AB中点,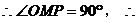 点M是在以OP为直径的圆周上,此圆的圆心为
点M是在以OP为直径的圆周上,此圆的圆心为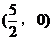 ,半径为
,半径为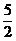 ,所以其方程为
,所以其方程为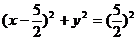 ,即
,即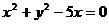 。同时,点M又在圆
。同时,点M又在圆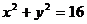 的内部,
的内部,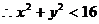 ,即
,即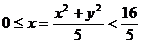 ,所以所求的轨迹方程为
,所以所求的轨迹方程为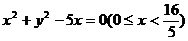
评注:此题若不能挖掘利用几何条件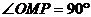 ,点M是在以OP为直径的圆周上,而利用参数方程等方法,计算量将很大,并且比较麻烦。
,点M是在以OP为直径的圆周上,而利用参数方程等方法,计算量将很大,并且比较麻烦。
例3. 求与 轴相切,圆心在直线
轴相切,圆心在直线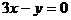 上,且被直线
上,且被直线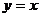 截得的弦长等于
截得的弦长等于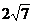 的圆的方程。
的圆的方程。
解:因圆心在直线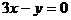 上,故可设圆心
上,故可设圆心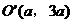
又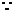 圆与
圆与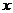 轴相切,
轴相切,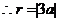 ,
,
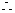 此时可设圆方程为
此时可设圆方程为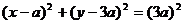
(运用已知条件,找出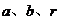 间联系,尽可能把未知量的个数减少,这对简化计算很有帮助。)
间联系,尽可能把未知量的个数减少,这对简化计算很有帮助。)
又圆被直线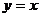 截得的弦长为
截得的弦长为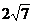 。考虑由圆半径、半弦、弦心距组成的直角三角形,只要将弦心距用
。考虑由圆半径、半弦、弦心距组成的直角三角形,只要将弦心距用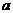 表示出来,便可利用勾股定理求得
表示出来,便可利用勾股定理求得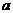 。
。
弦心距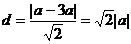
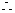
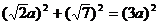 ,解得
,解得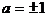
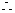 当
当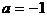 时,
时,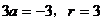 ,圆方程为
,圆方程为
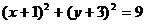
当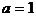 时,
时,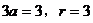 ,圆方程为
,圆方程为
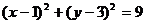
评注:此题若不充分利用圆的半径、半弦、弦心距组成的直角三角形,而用弦长公式,将会增大运算量。
例4. 设直线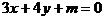 与圆
与圆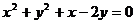 相交于P、Q两点,O为坐标原点,若
相交于P、Q两点,O为坐标原点,若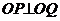 ,求
,求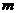 的值。
的值。
解: 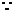 圆
圆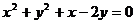 过原点,并且
过原点,并且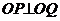 ,
,
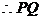 是圆的直径,圆心的坐标为
是圆的直径,圆心的坐标为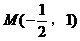
又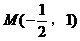 在直线
在直线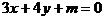 上,
上,
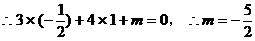 即为所求。
即为所求。
评注:此题若不充分利用一系列几何条件:该圆过原点并且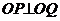 ,PQ是圆的直径,圆心在直线
,PQ是圆的直径,圆心在直线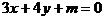 上,而是设
上,而是设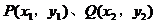 再由
再由 和韦达定理求
和韦达定理求 ,将会增大运算量。
,将会增大运算量。
我们经常设出弦的端点坐标而不求它,而是结合韦达定理求解,这种方法在有关斜率、中点等问题中常常用到。
例5. 已知中心在原点O,焦点在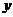 轴上的椭圆与直线
轴上的椭圆与直线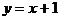 相交于P、Q两点,且
相交于P、Q两点,且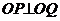 ,
,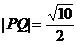 ,求此椭圆方程。
,求此椭圆方程。
解:设椭圆方程为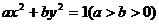 ,直线
,直线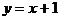 与椭圆相交于P
与椭圆相交于P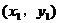 、
、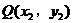 两点。
两点。
由方程组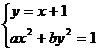 消去
消去 后得
后得
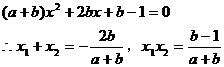
由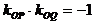 ,得
,得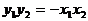 (1)
(1)
又P、Q在直线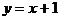 上,
上,
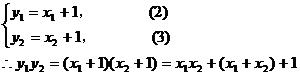
把(1)代入,得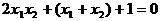 ,
,
即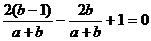
化简后,得
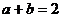 (4)
(4)
由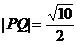 ,得
,得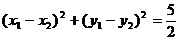
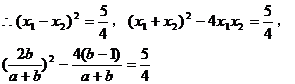
把(2)代入,得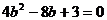 ,解得
,解得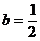 或
或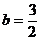
代入(4)后,解得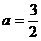 或
或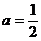
由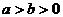 ,得
,得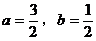 。
。
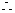 所求椭圆方程为
所求椭圆方程为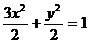
评注:此题充分利用了韦达定理及“设而不求”的策略,简化了计算。
例6. 若双曲线方程为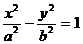 ,AB为不平行于对称轴且不过原点的弦,M为AB中点,设AB、OM的斜率分别为
,AB为不平行于对称轴且不过原点的弦,M为AB中点,设AB、OM的斜率分别为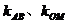 ,则
,则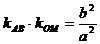
解:设A(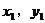 ),B(
),B(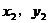 )则M(
)则M(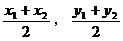 )
)
又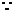 A、B分别在
A、B分别在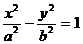 上,则有
上,则有
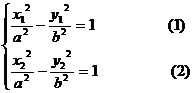
由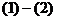 得
得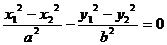 ,
,
即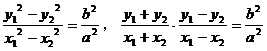 ,
,
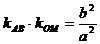
评注:此题充分利用了中点坐标公式斜率公式及“设而不求”的策略,简化了计算。
利用曲线系方程可以避免求曲线的交点,因此也可以减少计算。
例7. 求经过两已知圆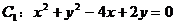 和
和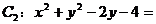 0的交点,且圆心在直线
0的交点,且圆心在直线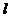 :
: 上的圆的方程。
上的圆的方程。
解:设所求圆的方程为:
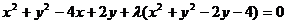
即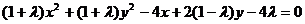 ,
,
其圆心为C(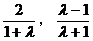 )
)
又C在直线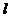 上,
上,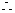
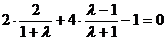 ,解得
,解得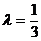 ,代入所设圆的方程得
,代入所设圆的方程得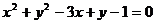 为所求。
为所求。
评注:此题因利用曲线系方程而避免求曲线的交点,故简化了计算。
近几年的高考数学试题,都有运算量大的特点,解析几何部分显得尤为突出,而在解析几何题中,又着重体现在求线段的长。若求线段长的计算方法不当,就会大大增加运算量,直接影响高考成绩。经笔者多年摸索,找到几种计算线段长的简便方法,写出来,供大家参考。
一般地,求直线与圆锥曲线相交的弦AB长的方法是:
把直线方程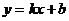 代入圆锥曲线方程中,得到型如
代入圆锥曲线方程中,得到型如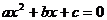 的方程,方程的两根设为
的方程,方程的两根设为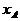 ,
,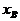 ,判别式为△,则
,判别式为△,则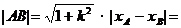
 。记住了结果 ,在计算中,直接代
。记住了结果 ,在计算中,直接代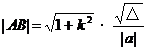 ,就能减少配方、开方等运算过程。
,就能减少配方、开方等运算过程。
例1 求直线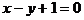 被椭圆
被椭圆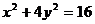 所截得的线段AB的长。
所截得的线段AB的长。
解:把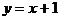 代入椭圆方程
代入椭圆方程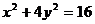 得到
得到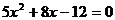 。
。
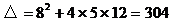 ,
,
则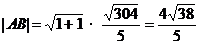 。
。
1. 求直线与圆的相交弦
因圆比较特殊,故求弦长不采用方法一,可用下面的方法,使运算简单。
设直线方程为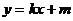 ,圆的方程为
,圆的方程为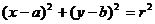 ,圆心为
,圆心为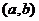 ,直线与圆相交于A、B,圆心到直线的距离为
,直线与圆相交于A、B,圆心到直线的距离为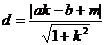 ,则
,则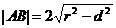 。
。
例2 求圆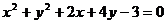 截得直线
截得直线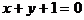 的线段长。
的线段长。
解:由原方程得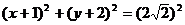 ,圆心为(-1,-2),则
,圆心为(-1,-2),则
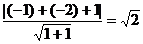 ,从而截得线段长
,从而截得线段长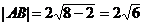 。
。
2. 求过圆锥曲线焦点的弦
圆锥曲线的定义都涉及焦点,结合图形运用圆锥曲线的定义,可回避复杂运算。
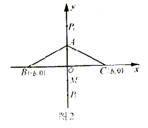
例3 如图1,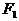 、
、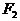 是椭圆
是椭圆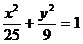 的两个焦点,AB是经过
的两个焦点,AB是经过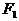 的弦,若
的弦,若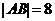 ,则
,则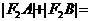 _______________。
_______________。
解:由定义可知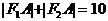 ,
,
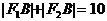 ,
,
则 。
。
又由图可知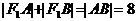 ,
,
因此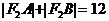 。
。
注:此题如果不结合图形用定义,就很难计算出结果。

3. 运用两种曲线组合构成的特殊位置关系,巧妙简化运算
例4 已知圆F的方程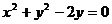 ,抛物线的顶点在原点,焦点是圆心F,过F引直线
,抛物线的顶点在原点,焦点是圆心F,过F引直线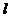 与抛物线和圆依次交于A、B、C、D四点,设
与抛物线和圆依次交于A、B、C、D四点,设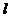 的倾斜角为
的倾斜角为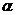 ,当
,当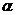 为何值时,线段
为何值时,线段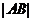 ,
,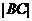 ,
,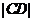 成等差数列。
成等差数列。
解:依题意知圆心F(0,1),半径为1,抛物线的方程: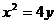 ,
,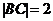 (如图2)。
(如图2)。
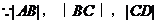 成等差数列,
成等差数列,
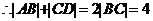 ,
,
即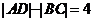 ,
,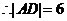 。
。
设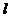 的方程为:
的方程为: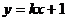 ,代入
,代入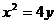 得
得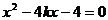 。
。
由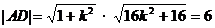 ,
,
解得 ,
,
故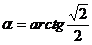 或
或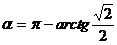 。
。
注:如果此题直接计算三段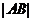 ,
,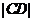 ,
,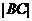 的长,而不结合图形得关系式
的长,而不结合图形得关系式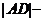
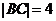 ,会加大运算量。
,会加大运算量。
1. 用三角形相似比,把平面上两点间的距离转化为数轴上两点间的距离
例5 直线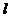 与
与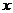 轴不垂直,与抛物线
轴不垂直,与抛物线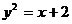 交于A、B两点,与椭圆
交于A、B两点,与椭圆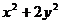
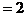 交于C、D两点,与
交于C、D两点,与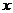 轴交于点
轴交于点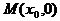 ,若
,若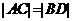 ,求
,求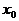 的范围。
的范围。
解:设直线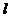 的方程为
的方程为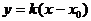 ,又设
,又设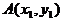 、
、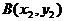
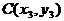 、
、
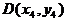 。
。
由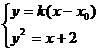 ,
,
得到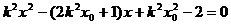 。
。
当 ,
(1)
,
(1)
由韦达定理得
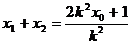 ,
,
由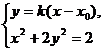
得到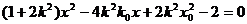 。
。
 (2)
(2)
有 。
。
要使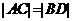 ,只需AB的中点与CD的中点坐标相同即可。由
,只需AB的中点与CD的中点坐标相同即可。由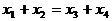 ,得
,得
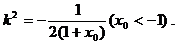 (3)
(3)
把(3)分别代入(1)、(2)可求得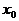 的范围为(-2,-1)。
的范围为(-2,-1)。
注:此题如果不转化,就找不到关系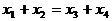 ,花费再多时间都难以解出。
,花费再多时间都难以解出。
2. 利用圆锥曲线的定义,把到焦点的距离转化为到准线的距离
例6 点A(3,2)为定点,点F是抛物线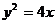 的焦点,点P在抛物线
的焦点,点P在抛物线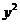
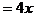 上移动,若
上移动,若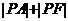 取得最小值,求点P的坐标。
取得最小值,求点P的坐标。
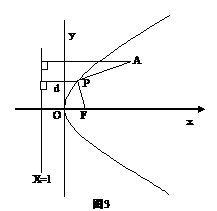
解:抛物线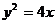 的准线方程为
的准线方程为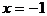 ,设P到准线的距离为
,设P到准线的距离为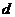 ,则
,则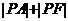
=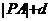 。要使
。要使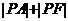 取得最小值,由图3可知过A点的直线与准线垂直时,
取得最小值,由图3可知过A点的直线与准线垂直时,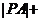
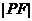 取得最小值,把
取得最小值,把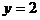 代入
代入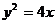 ,得P(1,2)。
,得P(1,2)。
利用直线参数方程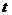 的几何意义,计算直线上经过同一点的两条线段的长。
的几何意义,计算直线上经过同一点的两条线段的长。
例7 过点A(-2,4)引倾斜角为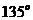 的直线交抛物线
的直线交抛物线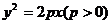 于
于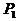
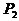 两点,若
两点,若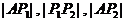 成等比数列,求P的值。
成等比数列,求P的值。
解:设直线的参数方程为
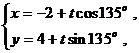
代入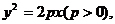 得
得
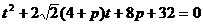 ,
,
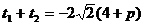 ,
,
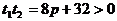 。
。
由参数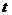 的几何意义,得
的几何意义,得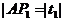 ,
,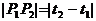 ,
,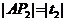 。
。
根据题意得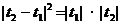 ,
,
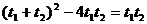 ,
,
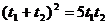 ,于是
,于是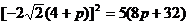 ,即
,即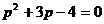 ,又
,又
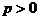 ,得
,得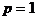 。
。
在过原点的几条线段成一定角的关系中,用极坐标会使运算简便。
例8 P、Q是双曲线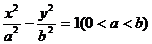 上的两点,若
上的两点,若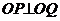 ,求证:
,求证:
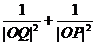 为定值。
为定值。
解:将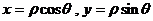 代入
代入
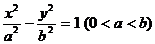 ,
,
有 。
。
设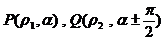 ,
,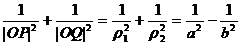 为定值。
为定值。
上面五种方法及例证充分说明,灵活掌握求线段长的简便算法,会加快你的解题速度,从而提高数学成绩,以利高考。
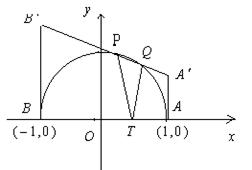
例1
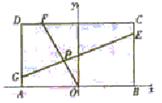
已知点T是半圆O的直径AB上一点,AB=2、OT=t (0<t<1),以AB为直腰作直角梯形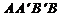 ,使
,使 垂直且等于AT,使
垂直且等于AT,使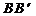 垂直且等于BT,
垂直且等于BT,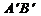 交半圆于P、Q两点,建立如图所示的直角坐标系.
交半圆于P、Q两点,建立如图所示的直角坐标系.
(1)写出直线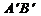 的方程;
的方程;
(2)计算出点P、Q的坐标;
(3)证明:由点P发出的光线,经AB反射后,反射光线通过点Q.
讲解: 通过读图, 看出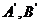 点的坐标.
点的坐标.
(1 ) 显然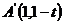 ,
, 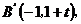 于是 直线
于是 直线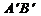
的方程为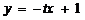 ;
;
(2)由方程组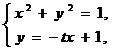
 解出
解出
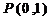 、
、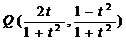 ;
;
(3)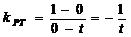 ,
,
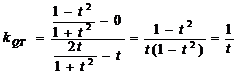 .
.
由直线PT的斜率和直线QT的斜率互为相反数知,由点P发出的光线经点T反射,反射光线通过点Q.
需要注意的是, Q点的坐标本质上是三角中的万能公式, 有趣吗?
例2
已知直线l与椭圆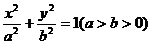 有且仅有一个交点Q,且与x轴、y轴分别交于R、S,求以线段SR为对角线的矩形ORPS的一个顶点P的轨迹方程.
有且仅有一个交点Q,且与x轴、y轴分别交于R、S,求以线段SR为对角线的矩形ORPS的一个顶点P的轨迹方程.
讲解:从直线 所处的位置, 设出直线
所处的位置, 设出直线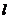 的方程,
的方程,
由已知,直线l不过椭圆的四个顶点,所以设直线l的方程为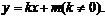
代入椭圆方程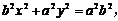 得
得
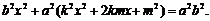
化简后,得关于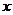 的一元二次方程
的一元二次方程
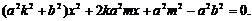
于是其判别式
由已知,得△=0.即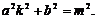 ①
①
在直线方程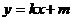 中,分别令y=0,x=0,求得
中,分别令y=0,x=0,求得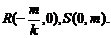
令顶点P的坐标为(x,y), 由已知,得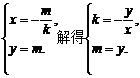
代入①式并整理,得
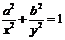 , 即为所求顶点P的轨迹方程.
, 即为所求顶点P的轨迹方程.
方程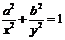 形似椭圆的标准方程, 你能画出它的图形吗?
形似椭圆的标准方程, 你能画出它的图形吗?
例3已知双曲线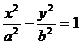 的离心率
的离心率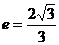 ,过
,过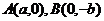 的直线到原点的距离是
的直线到原点的距离是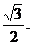
(1)求双曲线的方程;
(2)已知直线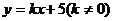 交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
讲解:∵(1)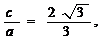 原点到直线AB:
原点到直线AB: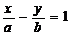 的距离
的距离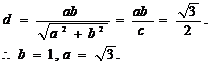 .
.
故所求双曲线方程为

(2)把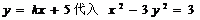 中消去y,整理得
中消去y,整理得 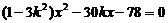 .
.
设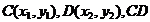 的中点是
的中点是 ,则
,则
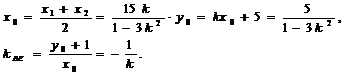
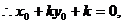
即
故所求k=±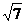 .
.
为了求出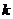 的值, 需要通过消元, 想法设法建构
的值, 需要通过消元, 想法设法建构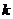 的方程.
的方程.
例4 已知椭圆C的中心在原点,焦点F1、F2在x轴上,点P为椭圆上的一个动点,且∠F1PF2的最大值为90°,直线l过左焦点F1与椭圆交于A、B两点,△ABF2的面积最大值为12.
(1)求椭圆C的离心率;
(2)求椭圆C的方程.
讲解:(1)设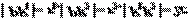 , 对
, 对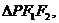 由余弦定理, 得
由余弦定理, 得
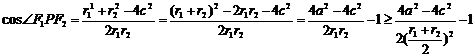
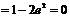 ,
,
解出
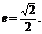
(2)考虑直线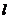 的斜率的存在性,可分两种情况:
的斜率的存在性,可分两种情况:
i) 当k存在时,设l的方程为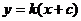 ………………①
………………①
椭圆方程为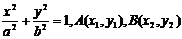
由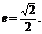 得
得 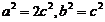 .
.
于是椭圆方程可转化为 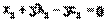 ………………②
………………②
将①代入②,消去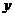 得
得 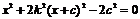 ,
,
整理为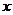 的一元二次方程,得
的一元二次方程,得 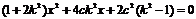 .
.
则x1、x2是上述方程的两根.且
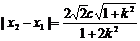 ,
,
|
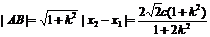 ,
,
 AB边上的高
AB边上的高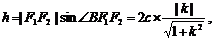
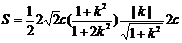
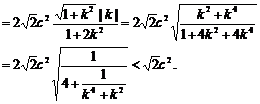
ii) 当k不存在时,把直线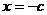 代入椭圆方程得
代入椭圆方程得
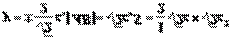
由①②知S的最大值为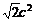 由题意得
由题意得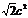 =12 所以
=12 所以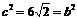
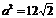
故当△ABF2面积最大时椭圆的方程为: 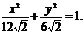
下面给出本题的另一解法,请读者比较二者的优劣:
设过左焦点的直线方程为: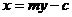 …………①
…………①
(这样设直线方程的好处是什么?还请读者进一步反思反思.)
椭圆的方程为: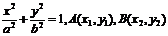
由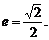 得:
得: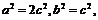 于是椭圆方程可化为:
于是椭圆方程可化为: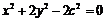 ……②
……②
把①代入②并整理得: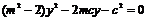
于是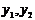 是上述方程的两根.
是上述方程的两根.
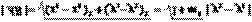
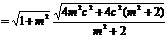
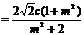 ,
,
AB边上的高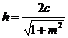 ,
,
从而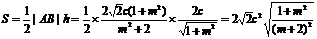
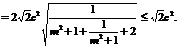
当且仅当m=0取等号,即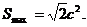
由题意知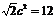 ,
于是
,
于是 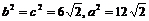 .
.
故当△ABF2面积最大时椭圆的方程为: 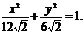
例5 已知直线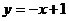 与椭圆
与椭圆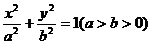 相交于A、B两点,且线段AB的中点在直线
相交于A、B两点,且线段AB的中点在直线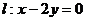 上.
上.
(1)求此椭圆的离心率;
(2 )若椭圆的右焦点关于直线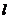 的对称点的在圆
的对称点的在圆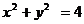 上,求此椭圆的方程.
上,求此椭圆的方程.
讲解:(1)设A、B两点的坐标分别为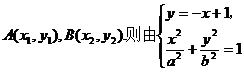 得
得

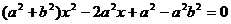 ,
,
根据韦达定理,得
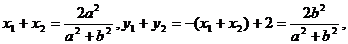
∴线段AB的中点坐标为(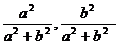 ).
).
由已知得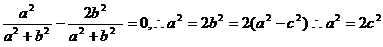
故椭圆的离心率为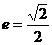 .
.
(2)由(1)知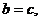 从而椭圆的右焦点坐标为
从而椭圆的右焦点坐标为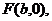 设
设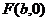 关于直线
关于直线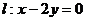 的对称点为
的对称点为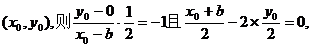
解得 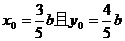
由已知得
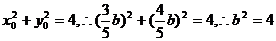
故所求的椭圆方程为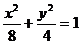 .
.
例6 已知⊙M: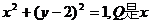 轴上的动点,QA,QB分别切⊙M于A,B两点,
轴上的动点,QA,QB分别切⊙M于A,B两点,
(1)如果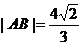 ,求直线MQ的方程;
,求直线MQ的方程;
(2)求动弦AB的中点P的轨迹方程.
讲解:(1)由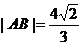 ,可得
,可得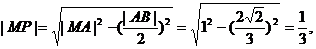 由射影定理,得
由射影定理,得 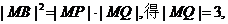 在Rt△MOQ中,
在Rt△MOQ中,
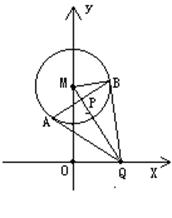
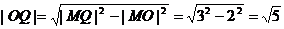 ,
,
故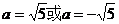 ,
,
所以直线AB方程是
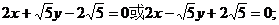
(2)连接MB,MQ,设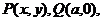 由
由
点M,P,Q在一直线上,得
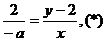 由射影定理得
由射影定理得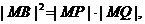
即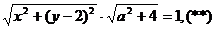 把(*)及(**)消去a,并注意到
把(*)及(**)消去a,并注意到 ,可得
,可得
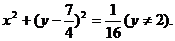
适时应用平面几何知识,这是快速解答本题的要害所在,还请读者反思其中的奥妙.
例7
如图,在Rt△ABC中,∠CBA=90°,AB=2,AC=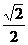 。DO⊥AB于O点,OA=OB,DO=2,曲线E过C点,动点P在E上运动,且保持|
PA |+| PB |的值不变.
。DO⊥AB于O点,OA=OB,DO=2,曲线E过C点,动点P在E上运动,且保持|
PA |+| PB |的值不变.
(1)建立适当的坐标系,求曲线E的方程;
(2)过D点的直线L与曲线E相交于不同的两点M、N且M在D、N之间,设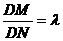 ,
,
试确定实数 的取值范围.
的取值范围.
讲解: (1)建立平面直角坐标系, 如图所示 .
 ∵| PA |+| PB |=| CA
|+| CB
|
y
∵| PA |+| PB |=| CA
|+| CB
|
y

|
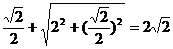
|
 ∴动点P的轨迹是椭圆 .
∴动点P的轨迹是椭圆 .

∵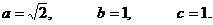
∴曲线E的方程是 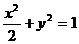 .
.
(2)设直线L的方程为
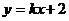 , 代入曲线E的方程
, 代入曲线E的方程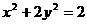 ,得
,得
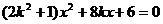
设M1(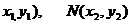 ,
则
,
则
|
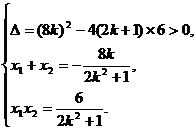
i) L与y轴重合时,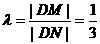
ii) L与y轴不重合时,
由①得 
又∵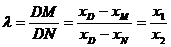 ,
,
∵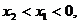 或
或 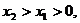
∴0< <1 ,
<1 ,
∴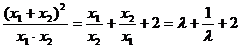 .
.
∵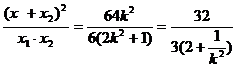
而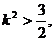 ∴
∴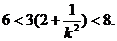
∴

∴
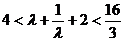 ,
, 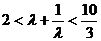 ,
,
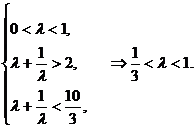
∴ 的取值范围是
的取值范围是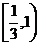 .
.
值得读者注意的是,直线L与y轴重合的情况易于遗漏,应当引起警惕.
例8
直线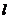 过抛物线
过抛物线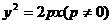 的焦点,且与抛物线相交于A
的焦点,且与抛物线相交于A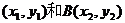 两点.
两点.
(1)求证: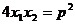 ;
;
(2)求证:对于抛物线的任意给定的一条弦CD,直线l不是CD的垂直平分线.
讲解: (1)易求得抛物线的焦点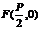 .
.
若l⊥x轴,则l的方程为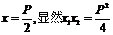 .
.
若l不垂直于x轴,可设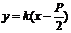 ,代入抛物线方程整理得
,代入抛物线方程整理得
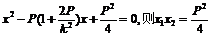 .
.
综上可知 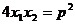 .
.
(2)设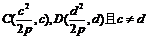 ,则CD的垂直平分线
,则CD的垂直平分线 的方程为
的方程为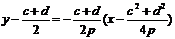
假设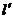 过F,则
过F,则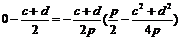 整理得
整理得
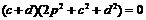
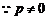
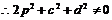 ,
,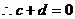 .
.
这时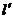 的方程为y=0,从而
的方程为y=0,从而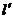 与抛物线
与抛物线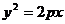 只相交于原点. 而l与抛物线有两个不同的交点,因此
只相交于原点. 而l与抛物线有两个不同的交点,因此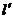 与l不重合,l不是CD的垂直平分线.
与l不重合,l不是CD的垂直平分线.
此题是课本题的深化,你能够找到它的原形吗?知识在记忆中积累,能力在联想中提升. 课本是高考试题的生长点,复课切忌忘掉课本!
例9 某工程要将直线公路l一侧的土石,通过公路上的两个道口A和B,沿着道路AP、BP运往公路另一侧的P处,PA=100m,PB=150m,∠APB=60°,试说明怎样运土石最省工?
讲解: 以直线l为x轴,线段AB的中点为原点对立直角坐标系,则在l一侧必存在经A到P和经B到P路程相等的点,设这样的点为M,则
|MA|+|AP|=|MB|+|BP|,
即 |MA|-|MB|=|BP|-|AP|=50,
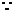
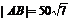 ,
,
∴M在双曲线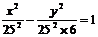 的右支上.
的右支上.
故曲线右侧的土石层经道口B沿BP运往P处,曲线左侧的土石层经道口A沿AP运往P处,按这种方法运土石最省工.
相关解析几何的实际应用性试题在高考中似乎还未涉及,其实在课本中还可找到典型的范例,你知道吗?
解析几何解答题在历年的高考中常考常新, 体现在重视能力立意, 强调思维空间, 是用活题考死知识的典范. 考题求解时考查了等价转化, 数形结合, 分类讨论, 函数与方程等数学思想, 以及定义法, 配方法, 待定系数法, 参数法, 判别式法等数学通法.
Ⅰ.求曲线的方程
1.曲线的形状已知
这类问题一般可用待定系数法解决。
例1 (1994年全国)
已知直线L过原点,抛物线C 的顶点在原点,焦点在x轴正半轴上。若点A(-1,0)和点B(0,8)关于L的对称点都在C上,求直线L和抛物线C的方程。
分析:曲线的形状已知,可以用待定系数法。
设出它们的方程,L:y=kx(k≠0),C:y2=2px(p>0).
设A、B关于L的对称点分别为A/、B/,则利用对称性可求得它们的坐标分别为:
A/(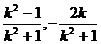 ),B/(
),B/(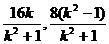 )。因为A/、B/均在抛物线上,代入,消去p,得:k2-k-1=0.解得:k=
)。因为A/、B/均在抛物线上,代入,消去p,得:k2-k-1=0.解得:k=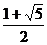 ,p=
,p=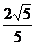 .
.
所以直线L的方程为:y=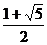 x,抛物线C的方程为y2=
x,抛物线C的方程为y2=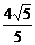 x.
x.
例2 (1993年全国)
在面积为1的△PMN中,tanM=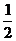 ,tanN=-2,建立适当的坐标系,求出以M、N为焦点且过点P的椭圆方程。
,tanN=-2,建立适当的坐标系,求出以M、N为焦点且过点P的椭圆方程。
分析:此题虽然与例1一样都是求形状已知的曲线方程问题,但不同的是例1是在给定的坐标系下求曲线的标准方程,而此题需要自己建立坐标系。为使方程简单,应以MN所在直线为x轴,以MN的垂直平分线为y轴。这样就可设出椭圆的标准方程,其中有两个未知数。
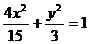
2.曲线的形状未知-----求轨迹方程
例3 (1994年全国)
 已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1,
动点M到圆C的切线长与|MQ|的比等于常数
已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1,
动点M到圆C的切线长与|MQ|的比等于常数 (
( >0),求动点M的轨迹方程,并说明它是什么曲线。
>0),求动点M的轨迹方程,并说明它是什么曲线。
分析:如图,设MN切圆C于点N,则动点M组成的集合是:
P={M||MN|= |MQ|},由平面几何知识可知:|MN|2=|MO|2-|ON|2=|MO|2-1,将M点坐标代入,可得:(
|MQ|},由平面几何知识可知:|MN|2=|MO|2-|ON|2=|MO|2-1,将M点坐标代入,可得:( 2-1)(x2+y2)-4
2-1)(x2+y2)-4 2x+(1+4
2x+(1+4 2)=0.
2)=0.
当 =1时它表示一条直线;当
=1时它表示一条直线;当 ≠1时,它表示圆。
≠1时,它表示圆。
这种方法叫做直接法。
 例4 (1999年全国)
例4 (1999年全国)
给出定点A(a,0)(a>0)和直线L:x=-1,B是直线L上的动点,∠BOA的角平分线交AB于点C,求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系。
分析:设C(x,y),B(-1,b).则直线OB的方程为:y=-bx.由题意:点C到OA、OB的距离相等,且点C在线段AB上,所以
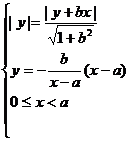
 y2[(1-a)x2-2ax+(1+a)y2]=0
y2[(1-a)x2-2ax+(1+a)y2]=0
若,y≠0,则(1-a)x2-2ax+(1+a)y2=0(0<x<a);若y=0,则b=0,∠AOB=180º,点C的坐标为(0,0),也满足上式。所以,点C的轨迹方程为(1-a)x2-2ax+(1+a)y2=0(0≤x<a)。
当a=1时,方程表示抛物线弧;当0<a<1时,方程表示椭圆弧;当a>1时,方程表示双曲线一支的弧。
一般地,如果选择了m个参数,则需要列出m+1个方程。
例5 (1995年全国)
已知椭圆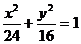 和直线L:
和直线L: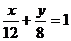 ,P是直线L上一点,射线OP交椭圆于点R,又点Q在OP上,且满足|OQ| |OP|=|OR|2,当点P在L上移动时,求点Q的轨迹方程,并说明轨迹是什么曲线。
,P是直线L上一点,射线OP交椭圆于点R,又点Q在OP上,且满足|OQ| |OP|=|OR|2,当点P在L上移动时,求点Q的轨迹方程,并说明轨迹是什么曲线。
分析:设Q(x,y),P(xP,yP),R(xR,yR), 则
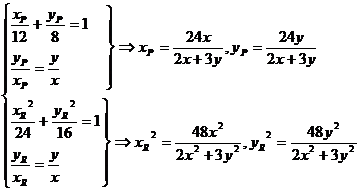 ,代入
,代入
 ,得:
,得: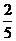 (x-1)2+
(x-1)2+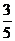 (y-1)2=1.
(y-1)2=1.
注意:若将点P、Q、R分别投影到x轴上,则式子 可用|x| |xP|=|xR2|代替,这样就简单多了。
可用|x| |xP|=|xR2|代替,这样就简单多了。
Ⅱ.研究圆锥曲线有关的问题
1.有关最值问题
例6 (1990年全国)
设椭圆中心为坐标原点,长轴在x上,离心率,已知点P(0,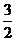 )到这个椭圆上的点的最远距离是
)到这个椭圆上的点的最远距离是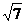 ,求这个椭圆方程,并求椭圆上到点P的距离等于
,求这个椭圆方程,并求椭圆上到点P的距离等于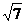 的点的坐标。
的点的坐标。
分析:最值问题,函数思想。关键是将点P到椭圆上点的距离表示为某一变量是函数,然后利用函数的知识求其最大值。
设椭圆方程为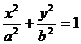 ,则由e=
,则由e=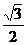 得:a2=4b2,所以x2=4b2-4y2.
得:a2=4b2,所以x2=4b2-4y2.
设Q(x,y)是椭圆上任意一点,则:
|PQ|=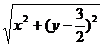 =
=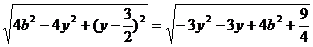 (-b
(-b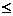 y
y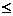 b).
b).
若b<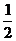 ,则-
,则-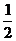 <-b,当y=-b时|PQ|max=
<-b,当y=-b时|PQ|max=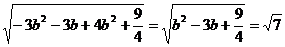 .
.
解得:b=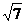 -
-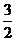 >
>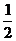 与b<
与b<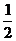 矛盾;若b
矛盾;若b
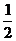 ,则当y=-
,则当y=-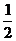 时|PQ|max=
时|PQ|max=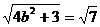 ,解得:b=1,a=2.
,解得:b=1,a=2.
2.有关范围问题
例7 (2001春季高考题)
已知抛物线y2=2px(p>0),过M(a,0)且斜率为1的直线L与抛物线交于不同的两点A、B,|AB|≤2p。
(1)求a的取值范围;
 (2)若线段AB的垂直平分线交x轴于点N,求△NAB面积的最大值。
(2)若线段AB的垂直平分线交x轴于点N,求△NAB面积的最大值。
分析:这是一道直线与圆锥曲线位置关系的问题,对于(1),可以设法得到关于a的不等式,通过解不等式求出a的范围,即:“求范围,找不等式”。或者将a表示为另一个变量的函数,利用求函数的值域求出a的范围;对于(2)首先要把△NAB的面积表示为一个变量的函数,然后再求它的最大值,即:“最值问题,函数思想”。
解:(1)直线L的方程为:y=x-a,将y=x-a 代入抛物线方程y2=2px,得:设直线L与抛物线两交点的坐标分别为A(x1,y1),B(x2,y2),则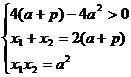 ,又y1=x1-a,y2=x2-a,
,又y1=x1-a,y2=x2-a,
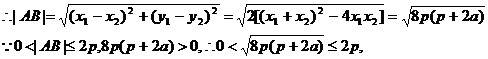 解得:
解得:
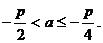
(2)设AB的垂直平分线交AB与点Q,令其坐标为(x3,y3),则由中点坐标公式得:

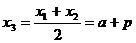 ,
,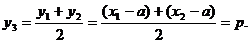
所以|QM|2=(a+p-a)2+(p-0)2=2p2.又△MNQ为等腰直角三角形,所以|QM|=|QN|=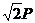 ,所以S△NAB=
,所以S△NAB=
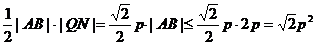 ,即△NAB面积的最大值为
,即△NAB面积的最大值为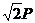 2。
2。
例8 (1992年高考题)
已知椭圆
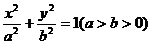 ,A,B是椭圆上的两点,线段AB的垂直平分线与x轴相交于点P(x0,0),证明:
,A,B是椭圆上的两点,线段AB的垂直平分线与x轴相交于点P(x0,0),证明:
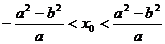 .
.
分析:欲证x0满足关于参数a、b的不等式,须从题中找出不等关系,由椭圆的性质可知,椭圆上的点的坐标满足如下条件:-a≤x≤a,因此问题转化为寻求x0与x的关系。
由题设知,点P在线段AB的垂直平分线上,所以|AP|=|BP|,若设A(x1,y1),B(x2,y2),则有:(x1-x0)2-y12=(x2-x0)2-y22,因为点A、B在椭圆上,所以,
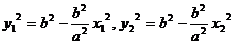 ,从而由-a≤x1≤a,-a≤x2≤a,可得:
,从而由-a≤x1≤a,-a≤x2≤a,可得:
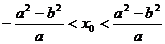
例9 (2000年高考题)
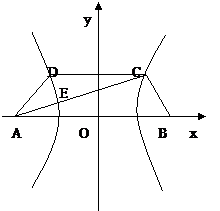
已知梯形ABCD中,|AB|=2|CD|,点E满足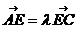 ,双曲线过C、D、E三点,且以A、B为焦点,当
,双曲线过C、D、E三点,且以A、B为焦点,当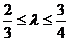 时,求双曲线离心率e的取值范围。
时,求双曲线离心率e的取值范围。
 分析:显然,我们只要找到e与
分析:显然,我们只要找到e与 的关系,然后利用解不等式或求函数的值域即可求出e的范围。
的关系,然后利用解不等式或求函数的值域即可求出e的范围。
解:如图建立坐标系,这时CD⊥y轴,
因为双曲线经过点C、D,且以A、B为焦点,由双曲线的对称性知C、D关于y轴对称。
依题意,记A(-C,0),C(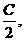 h),E(x0,y0),其中c=
h),E(x0,y0),其中c=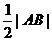 为双曲线的半焦距,h是梯形的高。
为双曲线的半焦距,h是梯形的高。
由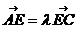 ,即(x0+c,y0)=
,即(x0+c,y0)=
 (
(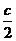 -x0,h-y0)得:x0=
-x0,h-y0)得:x0=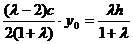 .设双曲线的方程为
.设双曲线的方程为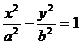 ,则离心率e=
,则离心率e=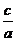 。由点C、E在双曲线上,将点C、E的坐标和e=
。由点C、E在双曲线上,将点C、E的坐标和e=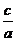 代入双曲线的方程得
代入双曲线的方程得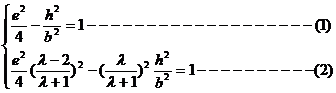
将(1)式代入(2)式,整理得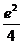 (4-4
(4-4 )=1+2
)=1+2 ,故
,故 =1
=1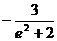 .
.
依题设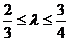 得
得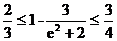 ,解得
,解得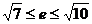 .
.
所以双曲线的离心率的取值范围是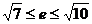 .
.
例10 已知抛物线y2=2px (p≠0)上存在关于直线x+y=1对称的相异两点,求p的取值范围。
分析:解决本题的关键是找到关于p的不等式。
设抛物线上关于直线x+y=1对称的两点是M(x1,y1)、N(x2,y2),设直线MN的方程为y=x+b.代入抛物线方程,得:x2+(2b-2p)x+b2=0.则x1+x2=2p-2b,y1+y2=( x1+x2)+2b=2p.则MN的中点P的坐标为 (p-b,p).因为点P在直线x+y=1上,所以2p- b=1,即b=2p-1。
又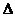 =(2b-2p)2-4b2=4p2-8bp>0,将b=2p-1代入得:4p2-8p(2p-1)>0,3p2-2p<0.解得:
=(2b-2p)2-4b2=4p2-8bp>0,将b=2p-1代入得:4p2-8p(2p-1)>0,3p2-2p<0.解得:
0<p< .
.
是否存在常数a、b、c,使函数f(x)=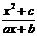 满足下列条件:
满足下列条件:
(1)函数f(x)是奇函数;
(2);f(1)<f(3) ;
(3)不等式0≤f(x)≤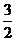 的解集是[-2,-1]∪[2,4]?
的解集是[-2,-1]∪[2,4]?
若存在,则求出不等式f(-2+sinθ) ≤m对任意θ∈R恒成立的实数m的取值范围;若不存在,说明理由。
解:由函数f(x)是奇函数得:b=0。又不等式0≤f(x)≤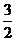 的解集是[-2,-1]∪[2,4],所以-2、-1、2、4是程f(x)=0与f(x)=
的解集是[-2,-1]∪[2,4],所以-2、-1、2、4是程f(x)=0与f(x)=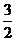 的根,从而:
的根,从而:
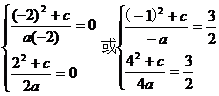 ,解得:a=2,c=-4,故:
,解得:a=2,c=-4,故:
f(x)= 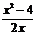 。
。
1.已知圆 的弦长为
的弦长为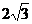 时,则a= ( C )
时,则a= ( C )
A.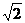 B.
B.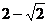 C.
C.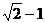 D.
D.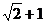
2.(03全国)已知双曲线中心在原点且一个焦点为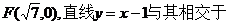 M、N两点,MN中点的横坐标为
M、N两点,MN中点的横坐标为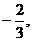 则此双曲线的方程是( D )
则此双曲线的方程是( D )
A.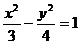 B.
B.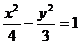
C.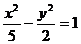 D.
D.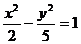
3 (03天津)不等式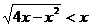 的解集是 ( C )
的解集是 ( C )
A.(0,2) B.(2,+∞)
C.(2,4) D.(-∞,0)∪(2,+∞)
4.(03天津)抛物线y=ax2 的准线方程是y=2,则a的值为 ( B )
A.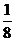 B.-
B.-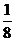 C.8 D.-8
C.8 D.-8
5(03江苏)如果函数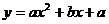 的图象与x轴有两上交点,则点(a,b)在aOb平面上的区
的图象与x轴有两上交点,则点(a,b)在aOb平面上的区
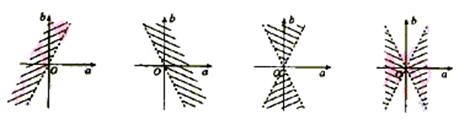 域(不包含边界)为 ( )C
域(不包含边界)为 ( )C
A. B. C. D.
6.(03江苏)抛物线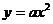 的准线方程是y=2,则a的值为 ( B )
的准线方程是y=2,则a的值为 ( B )
A.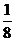 B.-
B.- C.8 D.-8
C.8 D.-8
7.(03江苏)设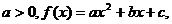 曲线
曲线 在点
在点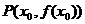 处切线的倾斜角的取值范
处切线的倾斜角的取值范
围为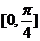 ,则P到曲线
,则P到曲线 对称轴距离的取值范围为 ( B )
对称轴距离的取值范围为 ( B )
A.[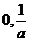 ] B.
] B.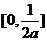 C.
C.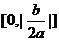 D.
D.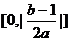
8.(03江苏)已知双曲线中心在原点且一个焦点为F(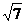 ,0)直线y=x-1与其相交于M、N两点,MN中点的横坐标为
,0)直线y=x-1与其相交于M、N两点,MN中点的横坐标为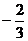 ,则此双曲线的方程是 ( D )
,则此双曲线的方程是 ( D )
A.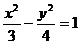 B.
B.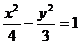 C.
C.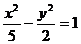 D.
D.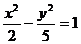
9.(03江苏)已知长方形四个顶点A(0,0),B(2,0),C(2,1)和D(0,1).一质点从AB的中点P0沿与AB夹角为θ的方向射到BC上的点P1后,依次反射到CD、DA和AB上的点P2、P3和P4(入射角等于反射角).设P4的坐标为(x4,0).若1< x4<2,则tanθ的取值范围是 ( C )
A.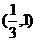 B.
B.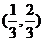 C.
C.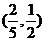 D.
D.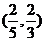
10(03广东)(双曲线虚轴的一个端点为M,两个焦点为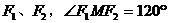 ,则双曲线的离心率为( )B
,则双曲线的离心率为( )B
A. 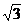 B.
B.
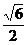 C.
C.
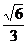 D.
D.
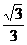
11 (03广东)(已知圆C: 及直线L:
及直线L: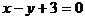 当直线L被C截得的弦长为23时,则
当直线L被C截得的弦长为23时,则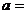 ( )C
( )C
A. 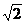 B.
B.
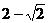 C.
C.
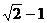 D.
D.
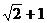
12(03广东)(不等式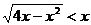 的解集是________
的解集是________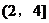
13. (03年上海)已知定点A(0,1),点B在直线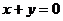 上运动,当线段AB最短时,点B的坐标是_________。
上运动,当线段AB最短时,点B的坐标是_________。 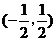
14. (03年上海)设集合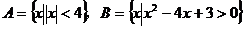 ,则集合
,则集合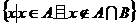 =__________________。
=__________________。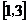
15(03年上海) 给出问题: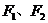 是双曲线
是双曲线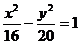 的焦点,点P在双曲线上。若点P到焦点F1的距离等于9,求点P到焦点F2的距离。某学生的解答如下:双曲线的实轴长为8,由
的焦点,点P在双曲线上。若点P到焦点F1的距离等于9,求点P到焦点F2的距离。某学生的解答如下:双曲线的实轴长为8,由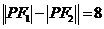 ,即
,即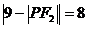 ,得
,得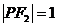 或17。
或17。
该学生的解答是否正确?若正确,请将他的解题依据填在下面空格内;若不正确,将正确结果填在下面空格内。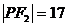
16(03年上海)(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分。
如图,某隧道设计为双向四车道,车道总宽22米,要求通行车辆限高4.5米,隧道全长2.5千米,隧道的拱线近似地看成半个椭圆形状。
(1)若最大拱高h为6米,则隧道设计的拱宽l是多少?
(2)若最大拱高h不小于6米,则应如何设计拱高h和拱宽l,才能使半个椭圆形隧道的土方工程量最小?
(半个椭圆的面积公式为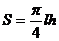 。柱体体积为:底面积乘以高。本题结果均精确到0.1米)
。柱体体积为:底面积乘以高。本题结果均精确到0.1米)

[解](1)如图建立直角坐标系,则点P(11,4.5)
椭圆方程为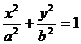
将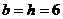 与点P坐标代入椭圆方程,得
与点P坐标代入椭圆方程,得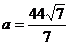 ,此时
,此时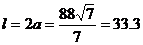
因此隧道的拱宽约为33.3米。
(2)[解一]由椭圆方程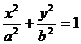
得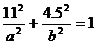
因为 ,即
,即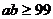 ,且
,且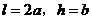
所以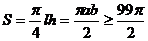
当S取最小值时,有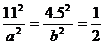 ,得
,得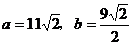
此时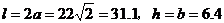
故当拱高约为6.4米,拱宽约为31.1米时,土方工程量最小
[解二]由椭圆方程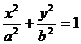 ,得
,得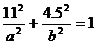
于是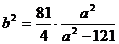

即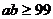 ,当S取最小值时,有
,当S取最小值时,有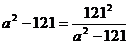
得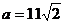 ,
,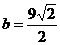 ,以下同解一
,以下同解一
17. (03年上海)(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分5分,第3小题满分7分。
在以O为原点的直角坐标系中,点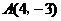 为
为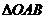 的直角顶点,已知
的直角顶点,已知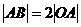 ,且点B的纵坐标大于零。
,且点B的纵坐标大于零。
(1)求向量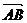 的坐标。
的坐标。
(2)求圆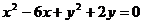 关于直线OB对称的圆的方程。
关于直线OB对称的圆的方程。
(3)是否存在实数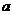 ,使抛物线
,使抛物线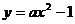 上总有关于直线OB对称的两个点?若不存在,说明理由;若存在,求
上总有关于直线OB对称的两个点?若不存在,说明理由;若存在,求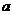 的取值范围。
的取值范围。
解](1)设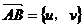 ,则由
,则由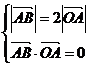 ,即
,即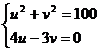 ,得
,得
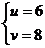 ,或
,或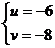
因为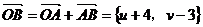
所以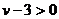 ,得
,得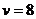 ,故
,故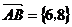
(2)由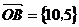 ,得B(10,5),于是直线OB方程:
,得B(10,5),于是直线OB方程: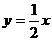
由条件可知圆的标准方程为: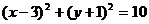
得圆心(3,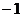 ),半径为
),半径为
设圆心(3,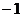 )关于直线OB的对称点为(x,y),则
)关于直线OB的对称点为(x,y),则
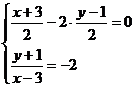 ,得
,得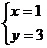
故所求圆的方程为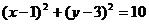
(3)设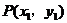 ,
,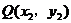 为抛物线上关于直线OB对称的两点,则
为抛物线上关于直线OB对称的两点,则
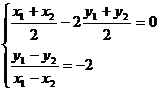 ,得
,得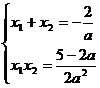
即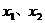 为方程
为方程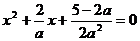 的两个相异实数
的两个相异实数
18.(03广东)(每小题满分14分)
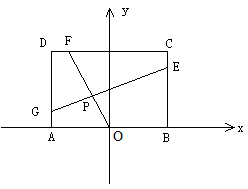
已知常数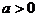 ,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且
,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且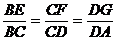 ,P为GE与OF的交点(如图)。问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由。
,P为GE与OF的交点(如图)。问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由。
解:根据题设条件,首先求出点P坐标满足的方程,据此再判定是否存在两定点,使得P到两定点距离的和为定值。
按题意有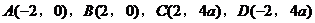
设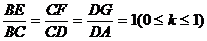
由此有
直线OF的方程为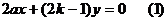
直线CE的方程为: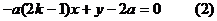
从(1)(2)消去参数k,得点P(x,y)坐标满足方程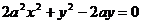
整理得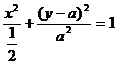
当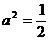 时,点P的轨迹为圆弧,所以不存在符合题意的两点。
时,点P的轨迹为圆弧,所以不存在符合题意的两点。
当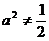 时,点P的轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长。
时,点P的轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长。
当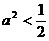 时,点P到椭圆两个焦点
时,点P到椭圆两个焦点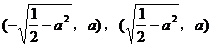 的距离之和为定值
的距离之和为定值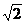
当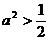 时,点P到椭圆两个焦点
时,点P到椭圆两个焦点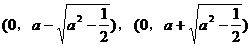 的距离之和为定值2a。
的距离之和为定值2a。
19.(03天津)(本小题满分14分)
已知常数a>0,向量c=(0,a),i=(1,0),经过原点O以c+λi为方向向量的直线与经过定点A(0,a)以i-2λc为方向向量的直线相交于点P,其中λ∈R.试问:是否存在两个定点E、F,使得|PE|+|PF|为定值.若存在,求出E、F的坐标;若不存在,说明理由.
20.本小题主要考查平面向量的概念和计算,求轨迹的方法,椭圆的方程和性质,利用方程判定曲线的性质,曲线与方程的关系等解析几何的基本思想和综合解题能力,满分14分。
解:根据题设条件,首先求出点P坐标满足的方程,据此再判断是否存在两定点,使得点P到两定点距离的和为定值.
∵i=(1,0),c=(0,a), ∴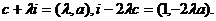
因此,直线OP和AP的方程分别为  y=ax和y-a=-2
y=ax和y-a=-2 ax .
ax .
消去参数 ,得点P(x,y)的坐标满足方程y (y-a)=-2a2x2 ,
,得点P(x,y)的坐标满足方程y (y-a)=-2a2x2 ,
整理得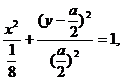 ①
①
因为a>0,所以得:
(i)当a=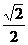 时,方程①是圆方程,故不存在合乎题意的定点E和F;
时,方程①是圆方程,故不存在合乎题意的定点E和F;
(ii)当0<a<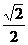 时,方程①表示椭圆,焦点E
时,方程①表示椭圆,焦点E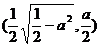 和
和
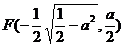 为合乎题意的两个定点;
为合乎题意的两个定点;
(iii)当a>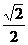 时,方程①表示椭圆,焦点E
时,方程①表示椭圆,焦点E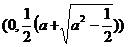 和F
和F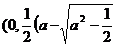 ))为合乎题意的两个定点.
))为合乎题意的两个定点.
21.(03天津)(本小题满分15分)
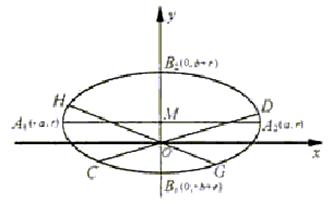
如图,椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心为M(0,r)(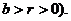
(Ⅰ)写出椭圆的方程,求椭圆的焦点坐标及离心率;
(Ⅱ)直线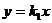 交椭圆于两点
交椭圆于两点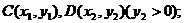 直线
直线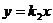 交椭圆于两点
交椭圆于两点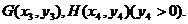 求证:
求证: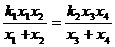 ;
;
(Ⅲ)对于(Ⅱ)中的C,D,G,H,设CH交x轴于点P,GD交x轴于点Q.
求证:|OP|=|OQ|. (证明过程不考虑CH或GD垂直于x轴的情形)
18.本小主要考查直线与椭圆等基本知识,考查分析问题和解决问题的能力.满分15分.
(Ⅰ)解:椭圆方程为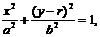 焦点坐标为
焦点坐标为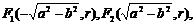
离心率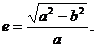
(Ⅱ)证明:将直线CD的方程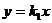 代入椭圆方程,得
代入椭圆方程,得
整理得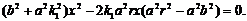 根据韦达定理,得
根据韦达定理,得
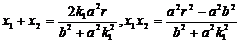 所以
所以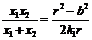 ①
①
将直线GH的方程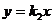 代入椭圆方程,同理可得
代入椭圆方程,同理可得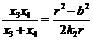 ,
,
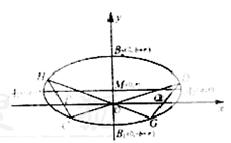 由①,②得
由①,②得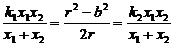 所以结论成立.
所以结论成立.
(Ⅲ)证明:设点P(p,0),点Q(q,0),由C、P、H共线,
得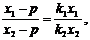 解得
解得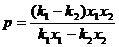 ,
,
由D、Q、G共线,同理可得
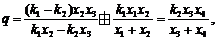
变形得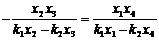
即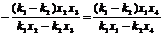
所以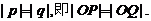
22.(03天津)(本小题满分14分)
有三个新兴城镇,分别位于A,B,C三点处,且AB=AC=a,BC=2b.今计划合建一个中心医院,为同时方便三镇,准备建在BC的垂直平分线上的P点处,(建立坐标系如图)
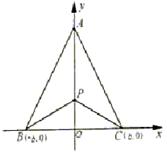 (Ⅰ)若希望点P到三镇距离的平方和为最小,
(Ⅰ)若希望点P到三镇距离的平方和为最小,
点P应位于何处?
(Ⅱ)若希望点P到三镇的最远距离为最小,
点P应位于何处?
23.(03天津)本小题主要考查函数,不等式等基本知识,考查运用数学知识分析问题和解决问题的能力.满分14分.
(Ⅰ)解:由题设可知,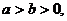 记
记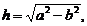 设P的坐标为(0,
设P的坐标为(0,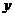 ),则P至三镇距离的平方和为
),则P至三镇距离的平方和为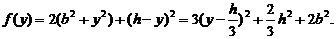 所以,当
所以,当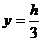 时,函数
时,函数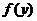 取得最小值. 答:点P的坐标是
取得最小值. 答:点P的坐标是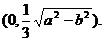
(Ⅱ)解法一:P至三镇的最远距离为 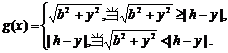
由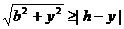 解得
解得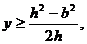 记
记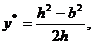 于是
于是
 当
当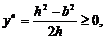 即
即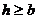 时,
时,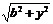 在[
在[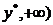 上是增函数,而
上是增函数,而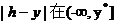 上是减函数. 由此可知,当
上是减函数. 由此可知,当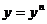 时,函数
时,函数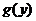 取得最小值. 当
取得最小值. 当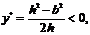 即
即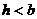 时,函数
时,函数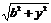 在[
在[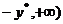 上,当
上,当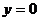 时,取得最小值
时,取得最小值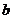 ,而
,而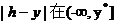 上为减函数,且
上为减函数,且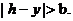 可见, 当
可见, 当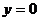 时, 函数
时, 函数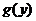 取得最小值. 答当
取得最小值. 答当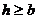 时,点P的坐标为
时,点P的坐标为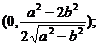 当
当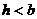 时,点P的坐标为(0,0),其中
时,点P的坐标为(0,0),其中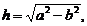
解法二:P至三镇的最远距离为 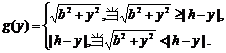 由
由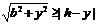 解得
解得
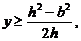 记
记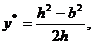 于是
于是

当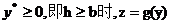 的图象如图
的图象如图 ,因此,当
,因此,当 时,函数
时,函数 取得最小值.
取得最小值.
 当
当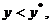 即
即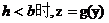 的图象如图
的图象如图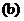 ,因此,当
,因此,当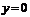 时,函数
时,函数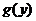 取得最小值.
取得最小值.
答:当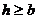 时,点P的坐标为
时,点P的坐标为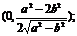 当
当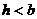 ,点P的坐标为(0,0),其中
,点P的坐标为(0,0),其中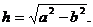
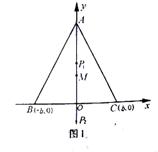
解法三:因为在△ABC中,AB=AC=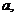 所以△ABC的外心M在射线AO上,其坐标为
所以△ABC的外心M在射线AO上,其坐标为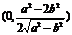 ,
,
 且AM=BM=CM. 当P在射线MA上,记P为P1;当P在射线MA的反向延长线上,记P为P2,
且AM=BM=CM. 当P在射线MA上,记P为P1;当P在射线MA的反向延长线上,记P为P2,
若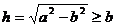 (如图1),则点M在线段AO上,
(如图1),则点M在线段AO上,
这时P到A、B、C三点的最远距离为
P1C和P2A,且P1C≥MC,P2A≥MA,所以点P与外心M
重合时,P到三镇的最远距离最小.
 若
若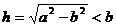 (如图2),则点M在线段AO外,这时
(如图2),则点M在线段AO外,这时
P到A、B、C三点的最远距离为P1C或P2A,
且P1C≥OC,P2A≥OC,所以点P与BC边中点O重合时,
P到三镇的最远距离最小为 .
.
答:当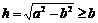 时,点P的位置在△ABC的外心
时,点P的位置在△ABC的外心
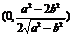 ;当
;当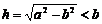 时,点P的位置在原点O.
时,点P的位置在原点O.
24.(03全国)(本小题满分14分)
 已知常数
已知常数 在矩形ABCD中,AB=4,BC=4
在矩形ABCD中,AB=4,BC=4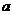 ,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且
,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且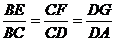 ,P为GE与OF的交点(如图),问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.
,P为GE与OF的交点(如图),问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.
21.根据题设条件,首先求出点P坐标满足的方程,据此再判断是否存在的两定点,使得点P到两点距离的和为定值.
按题意有A(-2,0),B(2,0),C(2,4a),D(-2,4a)设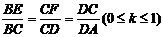
由此有E(2,4ak),F(2-4k,4a),G(-2,4a-4ak)直线OF的方程为: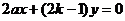 ①
①
直线GE的方程为: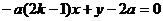 ②
②
从①,②消去参数k,得点P(x,y)坐标满足方程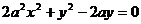
整理得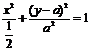 当
当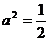 时,点P的轨迹为圆弧,所以不存在符合题意的两点.
时,点P的轨迹为圆弧,所以不存在符合题意的两点.
当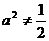 时,点P轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长。
时,点P轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长。
当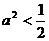 时,点P到椭圆两个焦点(
时,点P到椭圆两个焦点(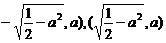 的距离之和为定值
的距离之和为定值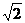 。
。
当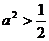 时,点P 到椭圆两个焦点(0,
时,点P 到椭圆两个焦点(0,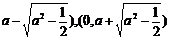 的距离之和为定值2
的距离之和为定值2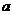 .
.
[模拟试题]
1. 过抛物线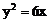 的焦点F,作弦
的焦点F,作弦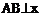 轴于A、B两点,则弦长
轴于A、B两点,则弦长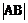 等于( )
等于( )
A. 6
B. 18 C. 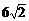 D.
36
D.
36
2. 若直线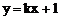 与焦点在x轴上的椭圆
与焦点在x轴上的椭圆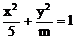 总有公共点,则实数m的取值范围是( )
总有公共点,则实数m的取值范围是( )
A. (0,5) B. (1,5) C. 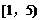 D.
D. 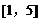
3. 直线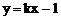 与抛物线
与抛物线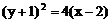 只有一个公共点,则k的值为________。
只有一个公共点,则k的值为________。
4. 直线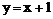 被椭圆
被椭圆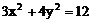 所截得的弦的中点坐标是( )
所截得的弦的中点坐标是( )
A. 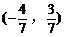 B.
B. 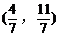 C.
C. 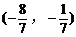 D.
D. 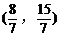
5. 过点A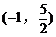 引抛物线
引抛物线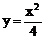 的一条弦,使该弦被A点平分,则该弦所在直线方程为(
)
的一条弦,使该弦被A点平分,则该弦所在直线方程为(
)
A. 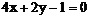 B.
B. 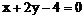
C. 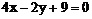 D.
D. 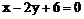
6. 曲线C: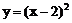 关于直线
关于直线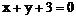 对称的曲线
对称的曲线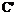 的方程_________。
的方程_________。
7. 设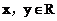 且
且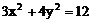 ,则
,则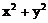 的最大值与最小值分别是( )
的最大值与最小值分别是( )
A. 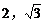 B.
B. 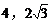 C. 4,3 D. 8,6
C. 4,3 D. 8,6
8. P是抛物线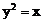 上的点,F是抛物线的焦点,则点P到F与P到A
上的点,F是抛物线的焦点,则点P到F与P到A 的距离之和的最小值是( )
的距离之和的最小值是( )
A. 3
B. 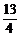 C.
4 D.
C.
4 D. 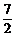
9. 已知抛物线C: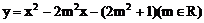
(1)求证:抛物线C与x轴交于一定点M;
(2)若抛物线与x轴正半轴交于N,与y轴交于P,求证:PN的斜率是一个定值;
(3)当m为何值时,三角形PMN的面积最小,并求此最小值。
高考数学总复习第六讲:解析几何 高考解析几何试题一般共有4题(2个选择题, 1个填空题, 1个解答题), 共计30分左右, 考查的知识点约为20个左右. 其命题一般紧扣课本, 突出重点, 全面考查. 选择题和填空题考查直线, 圆, 圆锥曲线, 参数方程和极坐标系中的基础知识. 解答题重点考查圆锥曲线中的重要知识点, 通过知识的重组与链接, 使知识形成网络, 着重考查直线与圆锥曲线的位置关系, 求解有时还要用到平几的基本知识, 这点值得考生在复课时强化.参考答案
[试题答案]
1. A 2.
C 3. 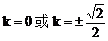 4.
A 5. B 6.
4.
A 5. B 6. 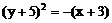
7. C 8. B
9. 证明:(1)令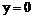 ,得
,得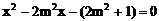
即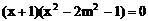
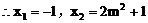
所以抛物线交x轴于定点M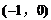
(2)由(1)知,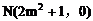 在抛物线方程中
在抛物线方程中
又令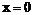 得
得
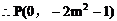
所以直线PN的斜率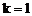 是一个定值。
是一个定值。
(3)由(2)知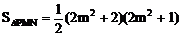
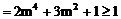
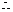 当
当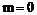 时,
时,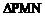 的面积最小,其最小面积为1。
的面积最小,其最小面积为1。