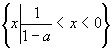例1:求函数求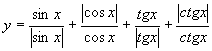 的值域.
分析:根据绝对值的定义
的值域.
分析:根据绝对值的定义
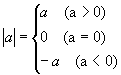 及题设中函数的表达式可知,要分别对绝对值号中的sinx,cosx,tgx,ctgx按照其大于零,小于零(不能为零)来讨论,以去掉绝对值号.而决定三角函数值正负的因素是角x所在的象限,故按角x的终边所在的象限为分类标准,进行分类讨论:
解 (1)角x在第一象限时,
及题设中函数的表达式可知,要分别对绝对值号中的sinx,cosx,tgx,ctgx按照其大于零,小于零(不能为零)来讨论,以去掉绝对值号.而决定三角函数值正负的因素是角x所在的象限,故按角x的终边所在的象限为分类标准,进行分类讨论:
解 (1)角x在第一象限时,
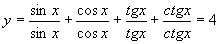 (2) 角x在第二象限时,
(2) 角x在第二象限时,
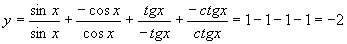 (3) 角x在第三象限时,
(3) 角x在第三象限时,
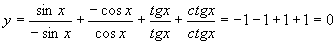 (4) 角x在第四象限时,
(4) 角x在第四象限时,
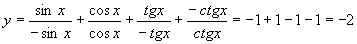 综上所述:函数的值域{4,0,-2}
说明:数学中的概念有些是含有不同种类的,当题目涉及这样的概念时,必须按给出概念的分类方式进行分类讨论,才能使解答完整无误.
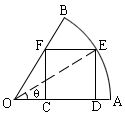
例2,已知扇形的圆心角为60°,半径为5cm,求这个扇形的内接长方形的最大面积.图
解:如图一,内接长方形CDEF的面积为:S=ED.EF ,
ED=OE.sinθ=5sinθ
在△EFO中,运用正弦定理,得
综上所述:函数的值域{4,0,-2}
说明:数学中的概念有些是含有不同种类的,当题目涉及这样的概念时,必须按给出概念的分类方式进行分类讨论,才能使解答完整无误.
例2,已知扇形的圆心角为60°,半径为5cm,求这个扇形的内接长方形的最大面积.图
解:如图一,内接长方形CDEF的面积为:S=ED.EF ,
ED=OE.sinθ=5sinθ
在△EFO中,运用正弦定理,得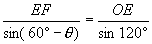 ∴
∴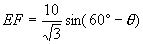 ∴
∴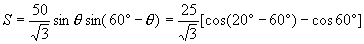 ∴
∴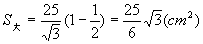 如图二.取
如图二.取  的中点M,连接OM分扇形为两个小扇形,在这二个小扇形中,各有原内接长方形的一半,∴内接长方形的面积为一个小扇形中内接长方形面积的2倍.
即
的中点M,连接OM分扇形为两个小扇形,在这二个小扇形中,各有原内接长方形的一半,∴内接长方形的面积为一个小扇形中内接长方形面积的2倍.
即
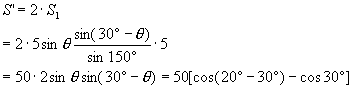 ∴
∴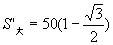
 再比较S大与S大′的大小
再比较S大与S大′的大小
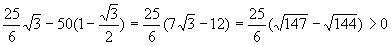
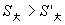
综上,所求扇形的最大内接长方形的面积为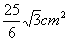 .
说明:本题是由图形的位置及形状不能确定引起的分类讨论,其原因在于扇形内接长方形相对于扇形的位置不确定,故而求出两种位置下的面积而后判断最大为多少.
例3 已知直角坐标平面上点Q(2,0)和圆C,x2+y2=1,动点M到圆C的切线长与|MQ|的比等于常数
.
说明:本题是由图形的位置及形状不能确定引起的分类讨论,其原因在于扇形内接长方形相对于扇形的位置不确定,故而求出两种位置下的面积而后判断最大为多少.
例3 已知直角坐标平面上点Q(2,0)和圆C,x2+y2=1,动点M到圆C的切线长与|MQ|的比等于常数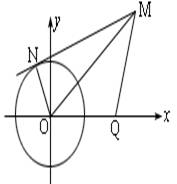 λ(λ>0)求动点M的轨迹方程,说明它表示什么曲线.
λ(λ>0)求动点M的轨迹方程,说明它表示什么曲线.
解 如图,设直线MN切圆O于N,则动点M组成的集合是
P={M||MN|=λ|MQ|}(其中λ>0)
∵圆半径|ON|=1,∴|MN|2=|MO|2-|ON|2=|MO|2-1
设点M的坐标为(x,y),则
 整理得:
整理得: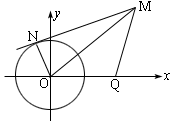
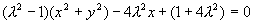
检验,坐标适合这个方程的点都属于集合P,故这个方程为所求的轨迹方程.
当λ=1时,方程化为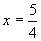 ,它表示一条直线,该直线与x轴垂直且交x轴于点
,它表示一条直线,该直线与x轴垂直且交x轴于点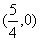 当λ≠1时,方程化为
当λ≠1时,方程化为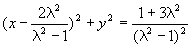 它表示圆,该圆圆心的坐标为
它表示圆,该圆圆心的坐标为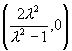 ,半径为
,半径为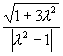 说明:本题在求出轨迹方程之后,在判定为何曲线时,因参数引起了分类讨论:一些问题中的数学表达式中因含有会导致不同结论的参数,从而需对参数分情况讨论为,求得问题的结果.
例4 已知a>1,解关于x的不等式:
说明:本题在求出轨迹方程之后,在判定为何曲线时,因参数引起了分类讨论:一些问题中的数学表达式中因含有会导致不同结论的参数,从而需对参数分情况讨论为,求得问题的结果.
例4 已知a>1,解关于x的不等式:
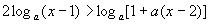 解:原不等式
解:原不等式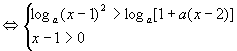
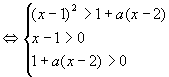
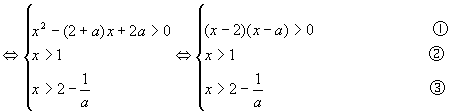 (i)当1<a<2时,由①得:x<a或x>2
∵
(i)当1<a<2时,由①得:x<a或x>2
∵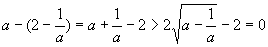 ∴
∴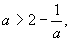 又∵
又∵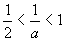 ∴
∴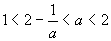 ∴解集为
∴解集为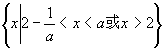 (ii)当a=2时,由①得x≠2,由③得
(ii)当a=2时,由①得x≠2,由③得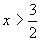 ∴解集为
∴解集为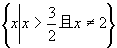 (iii)当a>2时,由①得,
x<2或x>a
∵
(iii)当a>2时,由①得,
x<2或x>a
∵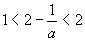 ∴解集为
∴解集为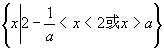 说明:本题中参数a,在求解集过程中,不同的取值,影响解集,故而要分类讨论,这是变形所需.
例5 某城市用水收费方法是:水费=基本费+超额费+排污费,若每月水量不超过最低限量am3时,只付基本费8元和每户每定额排污费c元;若用水量超过am3时,除了付给同上的基本费和排污费外,超过部分每方米付b元的超额费.已知每户每月的排污费不超过4元,该市一家庭今年第一季度的用水量和支付费用如下表所示:
解:设每月用水量为xm3,支付费用为y元.
则
说明:本题中参数a,在求解集过程中,不同的取值,影响解集,故而要分类讨论,这是变形所需.
例5 某城市用水收费方法是:水费=基本费+超额费+排污费,若每月水量不超过最低限量am3时,只付基本费8元和每户每定额排污费c元;若用水量超过am3时,除了付给同上的基本费和排污费外,超过部分每方米付b元的超额费.已知每户每月的排污费不超过4元,该市一家庭今年第一季度的用水量和支付费用如下表所示:
解:设每月用水量为xm3,支付费用为y元.
则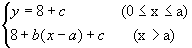
|
月份
|
用水量(m3)
|
水费(元)
|
|
1 |
8 |
9 |
|
2 |
15 |
19 |
|
3 |
13 |
15 |
由题意知0<c≤4,8+c≤12.
故第2、3月份用水量15
am3,13 am3大于最低用水限量am3
将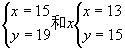 分别代入
分别代入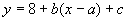 中,得
中,得
 ①
再分析1月份用水量是否超过最低限量am3
不妨设8>a,
将
①
再分析1月份用水量是否超过最低限量am3
不妨设8>a,
将 中,得
9=8+2(8–a)+c,
得2a=c+15 ②
∴1月份用水量不超过最低限量.
又∵y=8+c
∴9=8+c,c=1
∴a=10,b=2,c=1
说明:本题为实际应用问题,在解题过程中,隐含着分类讨论:a>8,a=8,a<8,根据条件,逐一讨论,使问题得以解决.
例6 设a>0,且a≠1,解关于x的不等式:
中,得
9=8+2(8–a)+c,
得2a=c+15 ②
∴1月份用水量不超过最低限量.
又∵y=8+c
∴9=8+c,c=1
∴a=10,b=2,c=1
说明:本题为实际应用问题,在解题过程中,隐含着分类讨论:a>8,a=8,a<8,根据条件,逐一讨论,使问题得以解决.
例6 设a>0,且a≠1,解关于x的不等式:
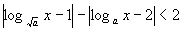 解:原不等式
解:原不等式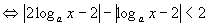 当0<a<1时,
原不等式
当0<a<1时,
原不等式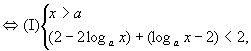 或(Ⅱ)
或(Ⅱ)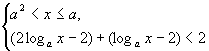 或(Ⅲ)
或(Ⅲ)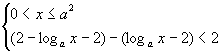 解不等式组(Ⅰ),得
解不等式组(Ⅰ),得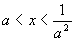 ;
解不等式组(Ⅱ),得
;
解不等式组(Ⅱ),得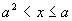 解不等式组(Ⅲ),无解.
∴原不等式的解集为
解不等式组(Ⅲ),无解.
∴原不等式的解集为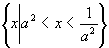 当a>1时,
原不等式
当a>1时,
原不等式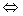 (Ⅰ)
(Ⅰ)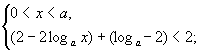 或(Ⅱ)
或(Ⅱ)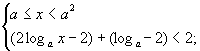 或(Ⅲ)
或(Ⅲ)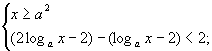 解不等式组(Ⅰ),得
解不等式组(Ⅰ),得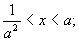 解不等式组(Ⅱ),得a≤x<a2;
不等式(Ⅲ)无解
∴原不等式的解集是
解不等式组(Ⅱ),得a≤x<a2;
不等式(Ⅲ)无解
∴原不等式的解集是 说明:本题在对a进行分类的过程中,又对x进行分类,以丢掉绝对值符号,是多次分类:
例7 设
说明:本题在对a进行分类的过程中,又对x进行分类,以丢掉绝对值符号,是多次分类:
例7 设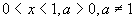 ,比较
,比较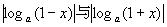 的大小.
分析:本题可用比差法,但要对a进行分类讨论,而用商比较法,可以不再进行分类讨论,解起来简单了.
解∵0<x<1
∴
的大小.
分析:本题可用比差法,但要对a进行分类讨论,而用商比较法,可以不再进行分类讨论,解起来简单了.
解∵0<x<1
∴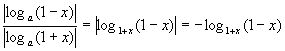
 ∴
∴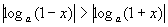 说明:分类讨论的目的是为了解决问题,但要视情况而定,若能不分类即可把问题解决就不要分类讨论
说明:分类讨论的目的是为了解决问题,但要视情况而定,若能不分类即可把问题解决就不要分类讨论
.1.已知不共面的三条直线a、b、c,a∥b∥c,过a作平面α,使b、c到α的距离相等,则满足条件的平面α有( )
(A)1个
(B)2个 (C)4个
(D)无数个
2.函数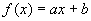 与它的反函数是同一函数的充要条件是( )
(A)a=1,b=0
(B) a=-1,b=0
(C)a=±1,b=0
(D)a=1,b=0 或a=-1,b∈R
3.已知k是常数,若双曲线
与它的反函数是同一函数的充要条件是( )
(A)a=1,b=0
(B) a=-1,b=0
(C)a=±1,b=0
(D)a=1,b=0 或a=-1,b∈R
3.已知k是常数,若双曲线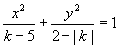 的焦距与k值R无关,则k的取值范围是(
)
(A)-2<k≤2
(B)k>5
(C)-2<k≤0
(D)0≤k<2
4.已知数列{an}前n次之和Sn满足
的焦距与k值R无关,则k的取值范围是(
)
(A)-2<k≤2
(B)k>5
(C)-2<k≤0
(D)0≤k<2
4.已知数列{an}前n次之和Sn满足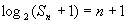 ,则an=_________.
5.直线m过点P(-2,1),点A(-1,-2)到直线m的距离等于1,则直线m的方程为________.
6.根据实数k的不同取值,讨论直线y=k(x+1)与双曲线
,则an=_________.
5.直线m过点P(-2,1),点A(-1,-2)到直线m的距离等于1,则直线m的方程为________.
6.根据实数k的不同取值,讨论直线y=k(x+1)与双曲线
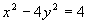 的公共点个数.
7.已知数列{an}和函数
的公共点个数.
7.已知数列{an}和函数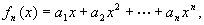 当n为正偶数时,
当n为正偶数时,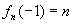 ;当n为 正奇数时,
;当n为 正奇数时,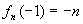 .求{an}的通项公式.
8.设a>0,a≠1,解关于x的不等式.
.求{an}的通项公式.
8.设a>0,a≠1,解关于x的不等式.
高考数学总复习第二讲:分类讨论 分类又称逻辑划分.分类讨论即是一种数学思维方法,也是一种重要的解题策略,常常能起到简化问题、解决问题的作用. 数字的解题过程,实质是一个变形过程,往往需要一些条件的限制,从而引起分类讨论. 分类讨论的关键问题就是:对哪个变量分类,如何分类. 分类的原则:由分类的定义,分类应满足下列要求: (1) 保证各类对象即不重复又不遗漏. (2) 每次分类必须保持同一分类标准. 应用分类讨论解决数学问题的一步骤: 参考答案
三、习题解答
1.B)提示:两种情况:过a与b、c所确定平面平行,或过a与b、c所确定平面相交.
2.选(D),提示: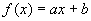 的反函数为
的反函数为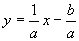 ,依题意
,依题意
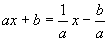 ∴
∴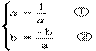 由①得a=±1,当a=1时,b=0,当a=
-1时,b∈R.
3.选(C)提示:表示双曲线,则
由①得a=±1,当a=1时,b=0,当a=
-1时,b∈R.
3.选(C)提示:表示双曲线,则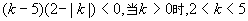 ,此时,
,此时,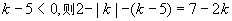 ,不合题意,当k≤0时,-2<k≤0,此时,
,不合题意,当k≤0时,-2<k≤0,此时,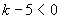 ,则
,则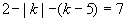 ,与k无关.
4.
,与k无关.
4.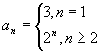 提示:由
提示:由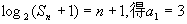 且
且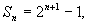 当n≥2时,
当n≥2时,
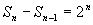 ,若
,若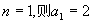 ,
∴
,
∴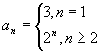 5.4x+3y+5=0,或x=-2
提示:直线m的斜率不存在时,方程为x=-1,满足条件,当斜率存在时,设其方程为y-1=k(x+2),由点到直线的距离公式,可得
5.4x+3y+5=0,或x=-2
提示:直线m的斜率不存在时,方程为x=-1,满足条件,当斜率存在时,设其方程为y-1=k(x+2),由点到直线的距离公式,可得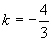 6.解:由
6.解:由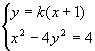 消去y整理得
消去y整理得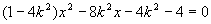 当
当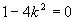 时,
时,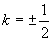 ,此时直线
,此时直线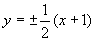 分别与双曲线的渐近线平行,它仍分别与双曲线的一支交于一点
当
分别与双曲线的渐近线平行,它仍分别与双曲线的一支交于一点
当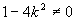 时,
时,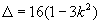 ∴当
∴当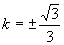 时,直线
时,直线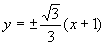 分别与双曲线只有一个公共点;
当
分别与双曲线只有一个公共点;
当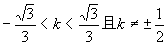 时,直线与双曲线有两个公共点;
当
时,直线与双曲线有两个公共点;
当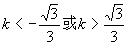 时,直线与双曲线无交点.
7.解 当n为正偶数时,
时,直线与双曲线无交点.
7.解 当n为正偶数时,
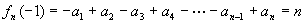 此时n-1为为正奇数,则
此时n-1为为正奇数,则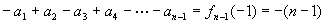 ∴
∴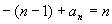 ∴
∴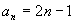 当n为正奇数时,(n>1)
当n为正奇数时,(n>1)
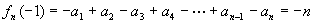 此时n-1为为正偶数,则
此时n-1为为正偶数,则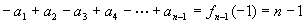 ∴
∴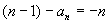 ,解得
,解得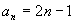 而当n=1时,由已知得
而当n=1时,由已知得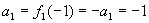 ∴
∴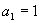 故数列
故数列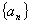 的通项公式为
的通项公式为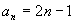 8.解:原不等式
8.解:原不等式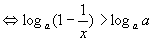 当
当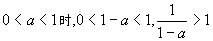 原不等式
原不等式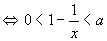
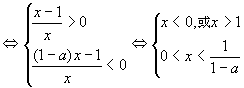 ∴原不等式的解集是
∴原不等式的解集是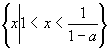 ;
当
;
当 原不等式
原不等式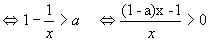
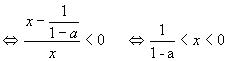 ∴原不等式的解集为
∴原不等式的解集为