向量考点有8个即:向量.向量的加法与减法,实数与向量的积.平面向量的坐标表示.线段的定比分点.平面向量的数量积.平面两点间的距离.平移.
除了平面向量的基本定理要求是了解,其余皆为理解与掌握.
三角有16个考点即:角的概念的推广.弧度制.任意角的三角函数.单位圆中的三角函数线.同角三角函数的基本关系式.正弦、余弦的诱导公式.两角和与差的正弦、余弦、正切.二倍角的正弦、余弦、正切.正弦函数、余弦函数的图象和性质.周期函数.正切函数的图象和性质.已知三角函数值求角.正弦定理.余弦定理.斜三角形解法.
三角考点与往年的区别不大,主要是删除应用计算器解三角形,而用计算器解三角形过去也从未考查.
考纲中明确要求⑴了解正弦函数余弦函数正切函数图象和性质, 会用描点法作图.但是大家都知道,近几年高考题对三角函数图象的考查却远远超出大纲中的要求.但对周期及最小正周期是了解.
⑵对和角与差角和倍角公式要求是掌握,近两年的高考试题在三角变换的要求明显降了下来.
从新教材开始的新高考命题统计看(见下表),对向量与三角的考查立足于基础题和中档题.位置一般在选择的前位和解答题的前三个.
04年全国14套试卷每一套解答题的第一题都是有关三角或向量,不是三角求值,就是三角函数,或向量与三角相结合.而小题主要是三角函数图象性质,或是利用诱导公式与倍角公式进行三角变形求值.但新教材与老教材最明显的区别就在于降低了三角变形要求.这在新高考中得到了充分的体现.
如03年江苏卷19题已知函数f(x)=sin(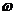
x+
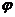
)是R上的偶函数,其图象关于点(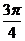
,0)对称,且在区间[0,
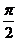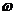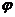]上是单调函数,求和的值
03新课程理17已知函数f(x)=2sinx(sinx+cosx)
Ⅰ、求函数f(x)的最小正周期和最大值
Ⅱ、在给出的坐标系中画出函数y=f(x)在区间[o,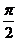]上的图象
(04天津17题)已知tan(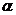
+
)=
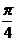Ⅰ、求tan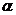值
Ⅱ、求
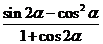的值
(04江苏17题)已知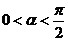
,
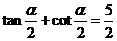,求
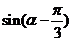的值.
以上考题,都表明了删除繁杂的三角变形,但三角公式还是要熟练的.如江苏17题若不知半角的切公式,应用常规的切化弦亦可以.从江苏03年的第19题可知对三角函数的要求却远远超出考纲中的了解.
向量是新增内容,从新高考命题思路看,主要是把向量作为工具与三角或解几立几相结合进行考查.或在小题中对向量的概念基本运算进行考查.命题的重点在向量的坐标式与向量的几何形式与向量的矢量式三种.
如去年(湖北的第19题)如图在Rt△ABC中, 已知BC=a,若长为2a的线段PQ以点A为中点,问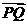
与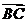
的夹角取何值时, 
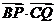的值最大并求出这个最大值.
(江苏16题)平面向量a,b中,已知a=(4,-3),|b|=1,且a•b=5则向量b.
这些考题说明对向量的要求围绕考纲要求设计考题.但向量的三种形式进行了全方位的考查.因此对向量的复习要围绕考纲进行设计试题.
|
|
2004年全理 |
2004全新理 |
2004天津 |
2004江苏 |
2003年新江苏 |
|
选择题 |
3(向量)、9(图象) |
5(切图象)、9(向量数量积)、10、11(周期) |
3(向量)、9(三角单调性)、12(周期应用) |
2 |
|
|
填空题 |
|
|
|
16(向量) |
|
|
解答题 |
17三角变形求值 |
17解三角形 |
17求值22向量与解几 |
17三角求值 |
|
纵观近三年的新教材考题,对三角的要求不会超出已有的水平,如三角变形,侧重于和差倍半,不是求值,就是解斜三角形.对三角函数的考查已远远超出考纲要求.即使考到也不会比较03年江苏试题19题难的.我个人认为应加大对斜三角形解法的关注度.
对向量的考查,仍然要关注向量的坐标运算和它们的几何意义,加强数与形相结合的关注度,同时也要对向量的矢量运算给以足够的重视.
由于这两章的知识考查的层次要求比较明确,因此在有限的第二轮复习中,对这两章的复习主要瞄准高考要求,不要盲目挖深,浪费不必要的宝贵时间.
① 立足小题,做好基本概念题.如三角函数定义与几何意义,三角求值三角函数图象及其性质等.而向量主要有向量的概念,及加减法的运算和几何意义实数与向量积的意义,向量数量积的运算及其几何意义等.
② 用专项训练的形式进行集中练习,通过练习,发现学生存在问题,针对存在的问题进行重点讲评,其后再编制纠正练习,让学生再练习.
③ 做好向量与解析几何的结合题,尤其是共线,定比分点等.主要复习措施教师要将这类题进行专题收集,学生进行专项练习,仍然要在做中找方法,提炼有效的解题思想与策略.
④ 做好向量在立几中的应用引导.因为我们选的是9.2A,没有空间向量知识,但是有的问题利用向量手段比较方便.但学生没有这方面的知识,如果你把这部分知识补充给学生,恐怕学生也难以做到应用自如.尤其空间几何体中没有空间直角坐标标架,点的坐标难以设定时.如何把握向量的科学应用的度?我个人认为:在异面直线所成角和垂直时应用向量的矢量式进行应用指导,鼓励学生在不好平移时,尤其是平移后的三角形不好解时应用.在探索性线线垂直或线面垂直应用向量的数量积进行探索.不涉及空间向量的坐标运算.
⒈高考题回顾.
(04全理9)为了得到函数y=sin(2x-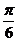
)的图象,可以将函数y=cos2x的图象
A向右平移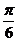个单位长度B向右平移
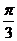个单位长度
C向左平移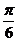个单位长度D向左平移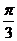个单位长度
(04福建理17)设函数f(x)=a.b,其中向量a=(2cosx,1),b=(cosx,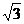
sin2x),x∈R.
Ⅰ、若f(x)=1-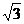且x∈[
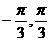],求x;
Ⅱ、若函数y=2sin2x的图象按向量c=(m,n)(|m|<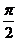)平移后得到函数y=f(x)的图象,求实数m,n的值.
从这两道高考原题,找到这两章复习的章法.解略.
⒉高考题选讲
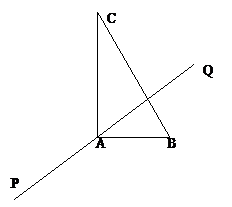
例1(04湖北理,19)如若图,在Rt△ABC中,已知BC=a,若长为2a的线段PQ以点A为中点,问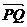
与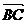
的夹角θ取何值时,
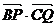的值最大?并求出这个最大值.
选此题意图是向量的矢量式运算法则,正是我们容易忽略的.去年湖北考生大多是应用向量的坐标运算，即建系设点，但是难在于如何将点P与点Q坐标表示出来.若能跳出坐标运算,选用向量的矢量式就容易多了.一方面这一题中人直角标架,学生容易切入.另一方面也说明向量的矢量式运算学生不习惯.
解
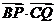
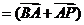
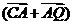
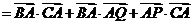
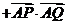
A为PQ的中点, 
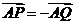
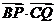=0+(
)
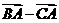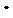
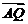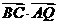-a2=
- a2=
-a2cosθ-
a2
故当θ=0°时最大,最大值为0.
思路二：以A为坐标原点以AB为x轴建立直角坐标系，则B(b,0),C(0,c),b2+c2=a2
设P(x,y)则Q点(-x,-y),x2+y2=a2
,
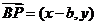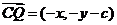
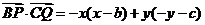=-x2-y2+bx-cy=
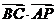-a2=a2cosθ-a2
下同前.
反思:
本题考查了向量的数量积运算,给出的形,要能把形转化成数,选择数量还是矢量,把学生的思维水平分成不同的层次.体现了命题人的良苦用心.
从学生的答题实际,反映了学生对向量学习的低层.除了坐标运算,不知坐标时,就无从下手,而这一题的关键在于对以A为中点条件处理直接决定了解题能否成功.而这正是学生转化的难点.平时在对学生训练时要给学生搭建‘数’与‘形’转化的桥梁.
例2(04天津理,17)已知tan(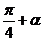
)=
,
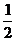求tan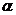的值;
求
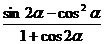的值.
分析:①利用两角和的正切公式即易求得tanα的值
②思路一:将sin2α,cos2α转化为α的单角形式,然后分子分母同除以cos2α,使表达式中只含tanα,再利用①可求得
思路二利用①的结果可得出sinα与cosα的一个等量关系,又sin2α+cos2α=1从而可求得cos2α的值而cos2α=2cos2α-1,sin2α=2sinα.cosα所以sin2αcos2α的值也可以求出.
思路三:可以先化简,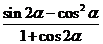 
再求值.
反思:本题考查了两角和的正切公式倍角公式同角关系等基础知识,考查了基本运算能力和基本方法.显然解题的入口宽,方法多,但是不同的方法所用的时间不一样,也反映了学生学习的层次.
因此在三角复习中,一定要学生有明确的变形方向,找到有效的方法,不能仅满足于会,在‘会’的基础上还要能‘优’.
例3(04北京15)在△ABC中,sinA+cosA=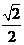
,AC=2,AB=3,求tanA的值和△ABC的面积.
此题是北京解答题的第一题,从它所处的位置可以知道属容易题.本题考查了解斜三角形.由已知sinA+cosA=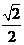可以求出tanA,再应用面积公式直接可以求出面积.从理论上是可行的,但实际状况学生由已知sinA+cosA=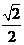,求不出sinA与cosA.因为数字不可爱.所以送分拿不到.
思路一:由sinA+cosA=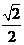两边平方可sin2A=-,从而可以得到sinA-cosA=
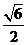,sinA=
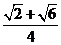,cosA=
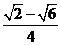,即可.
思路二:sin2A=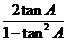
求出
⒊向量与解几的结合在解几中进行
⒋向量与立几结合
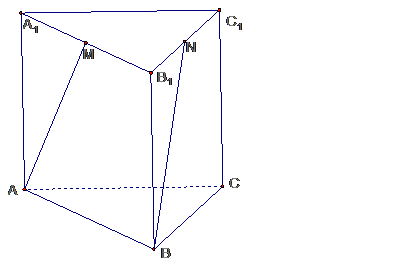
如图正三棱柱ABC-A1B1C1,侧棱AA1=2AB,MN分别是棱A1B1和B1C1的中点,求异面直线AM与BN所成角
若M为中点,N点在B1C1上移动,当N在何处时,AM⊥BN.
⒌1例题
2选题目的
3解
4解题回顾
wangaibin8978@