
1、(2002全国8)正六棱柱ABCDEF-A1B1C1D1E1F1底面边长为1,侧棱长为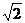 ,则这个棱柱的侧面对角线E1D与BC1所成的角是( )
,则这个棱柱的侧面对角线E1D与BC1所成的角是( )
A、90° B、60° C、45° D、30°
[评注]主要考查正六棱柱的性质,以及异面直线所成角的求法。
2、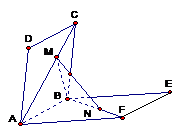 (2002全国18)如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=NB=a(0<a<
(2002全国18)如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=NB=a(0<a<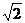 )
)
 (1)求MN的长;
(1)求MN的长;
(2)当a为何值时,MN的长最小;
(3)当MN长最小时,求面MNA与面
MNB所成的二面角的大小。
 [评注]考查线面关系,二面角函数最值等基础知识,考查空间想象力和推理能力。
[评注]考查线面关系,二面角函数最值等基础知识,考查空间想象力和推理能力。
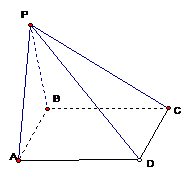
3、(2002全国19)如图,四棱锥P-ABCD的底面是边长为a的正方形,PB⊥面ABCD。
(1)若面PAD与面ABCD所成的二面角为60°,
求这个四棱锥的体积;
(2)证明无论四棱锥的高怎样变化,面PAD与面
PCD所成的二面角恒大于90°。
[评注]考查线面关系和二面角概念,以及空间想象力和逻辑推理能力。
4、(02全国文22)(一)给出两块面积相同的正三角形纸片,要求用其中一块剪拼成一个正三棱锥模型,使它们的全面积都与原三角形面积相等,请设计一种剪拼法,分别用虚线标示在图(1)(2)中,并作简要说明。

(二)试比较你剪拼的正三棱锥与正三棱柱的体积的大小。
(三)如果给出的是一块任意三角形的纸片,如图(3)要求剪拼成一个直三棱柱模型,使它的全面积与给出的三角形面积相等,请设计一种剪拼方法,用虚线标出在图3中,并作简要说明。
[评注]主要考查空间想象能力,动手操作能力,探究能力和灵活运用所学知识解决现实问题的能力。
5、(2002年上海14)已知直线l、m、平面α、β,且l⊥α,m β,给出下列四个命题。
β,给出下列四个命题。
(1)α∥β,则l⊥m (2)若l⊥m,则α∥β
(3)若α⊥β,则l∥m (4)若l∥m,则α⊥β
[评注]主要考查线面关系的判断。
6、(2002上海4)若正四棱锥的底面边长为2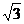 cm,体积为4cm3,则它的侧面与底面所成的二面角的大小是________.
cm,体积为4cm3,则它的侧面与底面所成的二面角的大小是________.
[评注]主要考查正棱锥中有关量的计算,以及二面角的求法。
7、(03全国15)在平面几何里,有勾股定理:“设△ABC的两边AB、AC互相垂直,则AB2+AC2=BC2”,拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面面积与底面积的关系,可以得出正确结论是:“设三棱锥A-BCD的一个侧面ABC、ACD、ADB两两互相垂直,则________”.
[评注]主要考查三棱锥基本知识,考查运用联想、类比、猜想的手法进行探索的能力。
8、(03年江苏7)棱长为a的正方体中,连结相邻面的中心,以这些线段为棱的八面体的体积为( )
A、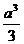 B、
B、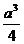 C、
C、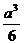 D、
D、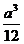
[评注]考查多面体积的计算方法。
9、(2003年江苏12)一个四面体的所有棱长都为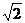 ,四个顶点在同一球面上,则此球的表面积为( )
,四个顶点在同一球面上,则此球的表面积为( )
A、3π B、4π C、3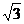 π D、6π
π D、6π
[评注]考查几何组合体知识以及多面体与球的计算问题。
10、对于四面体ABCD,给出下列四个命题①若AB=AC,BD=CD,则BC⊥AD;②若AB=CD,AC=BD,则BC⊥AD;③若AB⊥AC,BD⊥CD,则BC⊥AD;④AB⊥CD, BD⊥AC,则BC⊥AD;其中真命题的序号是_______________.
[评注]考查多面体中线线关系的判断。
11、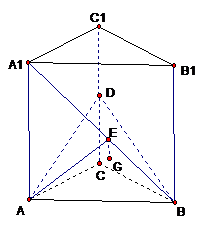 (2003年江苏19)如图,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD重心G。
(2003年江苏19)如图,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD重心G。
(1)求A1B与平面ABD所成的角大小;
(2)求点A1到平面AED的距离。
12、(2003年上海14)在下列条件中,可判断平面α与β平行的是( )
A、α、β都垂直于平面γ
B、α内存在不共线的三点到β的距离相等
C、l、m是α内两条直线,且l∥β,m∥β
D、l、m是两条异面直线,且l∥α,m∥α, l∥β,m∥β
[评注]主要考查线面、面面位置关系等基本知识,考查分析判断能力。
13、(2003年上海5)在正四棱锥P-ABCD中,若侧面与底面所成的二面角的大小为60°,则异面直线PA与BC所成角的大小等于____________.
[评注]主要考查异面直线所成角的度数的求法,正四棱锥的性质等基本知识,考查运算能力。
14、(2003年上海18)如图,已知平行六面体ABCD-A1B1C1D1中,A1A⊥平面ABCD,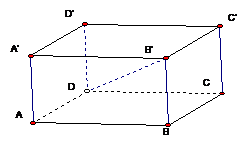 AB=4,AD=2,若B1D⊥BC,直线B1D与
AB=4,AD=2,若B1D⊥BC,直线B1D与
平面ABCD的所成的角等于30°,
求平行六面体ABCD-A1B1C1D1的体积。
[评注]主要考查平行六面体等基本知识。
15、(04年全国理16)已知a、b为不垂直的异面直线,α是一个平面,则a、b在α上的射影有可能的是
①两条平行直线 ②两条互相垂直的直线
③同一条直线 ④一条直线及其外一点
在上面结论中,正确结论的编号是_____________(写出所有正确结论的编号)
[评注]主要考查线面关系的判断。
16、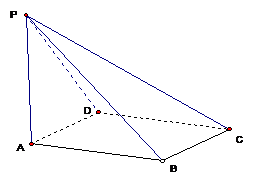 (04全国理20)如图,已知四棱锥P-ABCD,PB⊥AD,
(04全国理20)如图,已知四棱锥P-ABCD,PB⊥AD,
侧面PAD为边长等于2的正三角形,底面ABCD为菱形,
侧面PAD与底面ABCD所成的二面角为120°.
(1)求点P到平面ABCD的距离;
(2)求面APB与面CPB所成二面角的大小.
[评注]主要考查线面关系,点面距离及二面角的求法,以及空间想象力和逻辑推时能力。
17、(04全国理10)已知正四面体ABCD的表面积为S,其四个面的中心分别为E、F、G、H。设四面体EFGH的表面积为T,则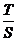 等于( )
等于( )
A、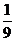 B、
B、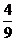 C、
C、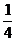 D、
D、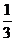
[评注]主要考查多面体表面积的求法。
18、(04江苏18)在棱长为4的正方体ABCD-A1B1C1D1中,O是正方形A1B1C1D1的中心,点P在棱CC1上,且CC1=4CP.
(1)求直线AP与平面BCC1B所成的角的大小(结果用反三角函数值表示);
(2)设O点在平面D1AP上射影是H,求证:D1H⊥AP;
(3)求点P到平面ABD1的距离.
[评注]本题主要考查线面角求法,线线垂直的判定方法,点面距及逻辑推理能力。
19、(04江苏4)一平面截一球得到直径是6cm的圆面,球心到这个平面的距离是4cm,则该球的体积是( )
A、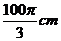 3 B、
3 B、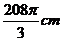 3
C、
3
C、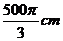 3
D、
3
D、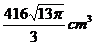
[评注]球的概念及性质,及球的体积计算公式。
二:近几年高考立几试题特点概述。
1,分值及难易程度。
近几年高考立几试题题量往往是两小(或三小)一大,均分在15到20多分之间,分值基本稳定,以容易题和中等题为主,偏难题一般作为选择题,大题都在前三题。考查方向始终把空间直线与直线、直线与平面、平面下平面的平行与垂直的性质与判定,考查的重点往往在角与距离的计算且算中有证。
(2)立几主客观题概述。
选择、填空题注重符号语言、文字语言、图形语言三种语言的相互转化,表现为对图形的识别,理解和加工。解答题形成一些规律,一般将几何元素集中于一个几何体中,即以一个多面体为依托,设置几个小问,设问形式以证明或计算为主。这方面上海高考卷普遍评价较好。从试卷命题来看,上海卷的立几部分也更体现上述精神,突出表现在:考查内容非常基本,各方面系数很稳定。选择题基本上考查线面关系的判定,更注重运用符号语言、文字语言、图形语言。今年取消了题型比例,上海高考卷更有研究的价值。希望大家更为关注。
(3)在稳定立体几何试题的同时,在创新方面也作了一些有益的尝试。如2003年把“平面勾股定理”拓展为“空间勾股定理”是首次出现的“研究性问题”,把平面几何题中的结论用模拟的方法推广到立体几何中,着重考查直觉、以及归纳猜想能力,由于考生平时少见少练这类试题,有利于推动研究性学习的开展,有利于营造公平竞争的环境,也有利于考查考试说明中新增的要求、即个性品质的要求。特别是在大题上进行了改革,使其更具有综合性、开放性,目的在于激发学生独立思考,从数学角度去发现和提出问题,并加以探索和研究,有利于提高学生的思维能力和创新意识,再者以立体几何题为试验,试图在改变试卷形式上有所突破。立体几何作为命题者的试验题,基本上每年都会出现。如2001年的第11题民房问题,2002年的第18题,综合运用代数函数求最值,2003年的第19题,借助于空间向量求角与距离,等等。
1、今年高考说明立几部分与04年相比,有几处小的调整。
①04年“了解三垂线定理及其逆定理” 05年改为“掌握三重线定理及逆定理。”
②今年删去了“了解多面体的欧拉公式”。
3“多面体,棱柱,棱锥,正多面体,球”调为“多面体,正多面体,棱柱,棱锥,球”
2、分析考试说明立几部分,命题内容虽有小的调整,但仍保持一定的稳定性与连续性,考查的重点仍是点线面的位置关系及空间距离和空间角,突出空间想象能力,突出突间图形的特点,侧重于空间元素位置关系和定性与定量考查。
3、立体几何第一部分线面关系的内容要求全是“掌握”,而第二部分很多概念只需“了解”,如多面体、凸面体、正多面体的概念,球的概念,要“掌握”的主要是这些几何体的性质以及球的表面积与体积公式。二轮复习重点仍在第一部分不能动摇。
4、纵观近几年高考立几部分相对比较稳定,高考试题中没有出现运用所学的立体几何知识来分析和解决较为复杂的和综合性的问题。我认为这种命题的格局今年仍不会改变。当然,不排除用其他知识来解决立体几何问题,如用代数知识来解决立几中的最值问题,也可综合运用三角、排列组合方法来解决立几中的其它问题等。
5、根据近几年高考立几解答题所选载体看,主要还是以常见的三棱柱,四棱柱,三棱锥,四棱锥为主,但要关注非常规放置问题,也要兼顾非规则多面体模型,由于江苏各所学校所选教材的具体情况不同而且近两年也不是以二选一模式,故解答题应是既能用空间向量知识解也能用传统知识解。平时在教学时留心三线垂直问题。
6、欧拉公式不会考。
1、二轮复习紧紧抓住立几第一部分不动摇,除了突出知识的主干体系,让学生整体把握好所学知识外,还应突出重点,不必面面俱到。复习时可安排三课时左右,集中解决三类问题:一是线面、面面关系;二是空间角;三是距离、面积与体积的计算,关注用代数方法解决立几的最值问题。
2、二轮复习更应注重变式训练,拓展,举一反三,在激发学生学习兴趣的同时,增加了容量,拓展了学生的思维空间。由于时间紧,任务重,更要注意时间的有效利用,比如为减少课堂画图时间,我们可以用一个四面体为载体,解决一系列问题,包括特征图形、特殊几何体,共点、共线、共面问题,线面关系的判定问题,各种角与距离、面积与体积的计算问题,“割”与“补”的方法,一些重点结论(公式)的问题,如cosα=cosβcosγ,cosα=s' /s,l2=a2+b2+c2等等,以基本图形带动一系列知识的复习,达到系统复习内容、突出重点的目的。
3、二轮复习是“转化”与“降维”思想, “割”与“补”思想的综合运用阶段。 “转化”思想,①常用等角定理或平行移动直线及平面的方法转化为所求角的位置,②常用平行线面间或平行平面间的距离相等为依据,转化为所求距离的位置,③常用割补法或等积变换解决有关距离或体积问题。
另外空间向量作为一种工具还会考查,或许会以定义形式给出来解决立体几何问题,所以对于平面向量与空间向量应当适当给予关注。
4、针对高考中常以判断题的形式考查元素关系问题,要在复习中运用运动变化的思想,让点或直线或平面在满足条件的情况下充分运动,要注意对定理条件的加强或减弱的变化来考查元素位置关系的变化,要注意考察其逆命题、否命题的对与错。通过反复比较分清是非。针对大题中的线面关系的证明题,要注意线线、线面、面面关系的相互转化,用定理时要先申明条件,再由定理得出相应的结论。作为空间中线面角与距离的计算,要明确角或距离的位置,学会用平移和补形的方法来寻找,尤其注意两“足”(斜足和垂足)的应用,而垂足的寻找通常用到面面垂直的性质定理,作为三垂线定理及其逆定理的运用,特别在求线与面成角和二面角时往往用此定理,先设法确定面的垂线,搭建用三垂线定理的结构。另外立体几何中的组合体问题近几年也常考,特别是球内的组合体问题,我们复习时要引导学生能认清基本图形,能画出截面图,并根据截面图来研究组合体中各元素的关系。还有图形的变化,特别是翻折与展开的问题,也应予适当的重视。
5、二轮复习,我们也要注意关注、搜集、分析学生一轮复习的学情,针对出现的问题做到有的放矢的复习并进行强化训练。
6、规范书写、应对网上阅卷
今年网上阅卷的选择题、填空题、解答题书写在一份答卷纸上,与以往高考的答题模式不一样。为了便于网上阅卷,要求考生在做图和书写时,要用50毫米的黑色签字笔,希望考生要强化适应训练。因为,高考的得分是以学生的书写为依据,书写规范不规范,会不会书写直接影响高考的评分。 五附三课时教案
垂直与平行
垂直与平行是高考的重点内容之一,考查内容灵活多样.本节主要帮助考生深刻理解线面平行与垂直、面面平行与垂直的判定与性质,并能利用它们解决一些问题.
例一:选择题与填空题
1.在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为4,则点A1到截面AB1D1的距离是( )
A.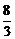 B.
B.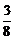 C.
C.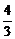 D.
D.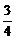
解析:如图,设A1C1∩B1D1=O1,∵B1D1⊥A1O1,B1D1⊥AA1,∴B1D1⊥平面AA1O1,故平面AA1O1⊥AB1D1,交线为AO1,在面AA1O1内过A1作A1H⊥AO1于H,则易知A1H长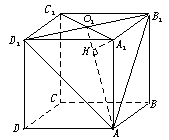 即是点A1到平面AB1D1的距离,在Rt△A1O1A中,A1O1=
即是点A1到平面AB1D1的距离,在Rt△A1O1A中,A1O1=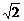 ,AO1=3
,AO1=3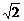 ,由A1O1.A1A=h.AO1,可得A1H=
,由A1O1.A1A=h.AO1,可得A1H=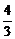 .
.
答案:C
2.在直二面角α-l-β中,直线a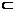 α,直线b
α,直线b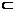 β,a、b与l斜交,则( )
β,a、b与l斜交,则( )
A.a不和b垂直,但可能a∥b B.a可能和b垂直,也可能a∥b
C.a不和b垂直,a也不和b平行 D.a不和b平行,但可能a⊥b
2.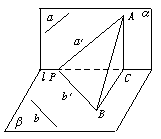 解析:如图,在l上任取一点P,过P分别在α、β内作a′∥a,b′∥b,在a′上任取一点A,过A作AC⊥l,垂足为C,则AC⊥β,过C作CB⊥b′交b′于B,连AB,由三垂线定理知AB⊥b′,∴△APB为直角三角形,故∠APB为锐角.
解析:如图,在l上任取一点P,过P分别在α、β内作a′∥a,b′∥b,在a′上任取一点A,过A作AC⊥l,垂足为C,则AC⊥β,过C作CB⊥b′交b′于B,连AB,由三垂线定理知AB⊥b′,∴△APB为直角三角形,故∠APB为锐角.
答案:C
3设X、Y、Z是空间不同的直线或平面,对下面四种情形,使“X⊥Z且Y⊥Z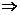 X∥Y”为真命题的是_________(填序号).
X∥Y”为真命题的是_________(填序号).
①X、Y、Z是直线 ②X、Y是直线,Z是平面 ③Z是直线,X、Y是平面 ④X、Y、Z是平面
、3.解析:①是假命题,直线X、Y、Z位于正方体的三条共点棱时为反例,②③是真命题,④是假命题,平面X、Y、Z位于正方体的三个共点侧面时为反例.
答案:②③
4.设a,b是异面直线,下列命题正确的是__.④_______.
①过不在a、b上的一点P一定可以作一条直线和a、b都相交
②过不在a、b上的一点P一定可以作一个平面和a、b都垂直
③过a一定可以作一个平面与b垂直
④过a一定可以作一个平面与b平行
例二:两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB,且AM=FN,求证:MN∥平面BCE.
命题意图:本题主要考查线面平行的判定,面面平行的判定与性质,以及一些平面几何的知识。
知识依托:解决本题的关键在于找出面内的一条直线和该平面外的一条直线平行,即线(内)∥线(外)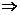 线(外)∥面.或转化为证两个平面平行.
线(外)∥面.或转化为证两个平面平行.
技巧与方法:证法一利用线面平行的判定来证明.证法二采用转化思想,通过证面面平行来证线面平行.
证法一:作MP⊥BC,NQ⊥BE,P、Q为垂足,则MP∥AB,NQ∥AB.
∴MP∥NQ,又AM=NF,AC=BF,
∴MC=NB,∠MCP=∠NBQ=45°
∴Rt△MCP≌Rt△NBQ
∴MP=NQ,故四边形MPQN为平行四边形
∴MN∥PQ
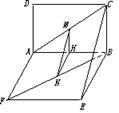
∵PQ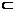 平面BCE,MN在平面BCE外,
平面BCE,MN在平面BCE外,
∴MN∥平面BCE.
证法二:如图过M作MH⊥AB于H,则MH∥BC,
∴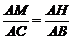
连结NH,由BF=AC,FN=AM,得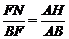
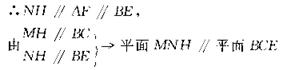
∴MN∥平面BCE.
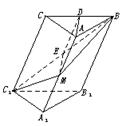 [例2]在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.
[例2]在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.
(1)若D是BC的中点,求证:AD⊥CC1;
(2)过侧面BB1C1C的对角线BC1的平面交侧棱于M,若AM=MA1,求证:截面MBC1⊥侧面BB1C1C;
(3)AM=MA1是截面MBC1⊥平面BB1C1C的充要条件吗?请你叙述判断理由.
命题意图:本题主要考查线面垂直、面面垂直的判定与性质,
知识依托:线面垂直、面面垂直的判定与性质.
技巧与方法:本题属于知识组合题类,关键在于对题目中条件的思考与分析,掌握做此类题目的一般技巧与方法,以及如何巧妙作辅助线.
(1)证明:∵AB=AC,D是BC的中点,∴AD⊥BC
∵底面ABC⊥平面BB1C1C,∴AD⊥侧面BB1C1C
∴AD⊥CC1.
(2)证明:延长B1A1与BM交于N,连结C1N
∵AM=MA1,∴NA1=A1B1
∵A1B1=A1C1,∴A1C1=A1N=A1B1
∴C1N⊥C1B1
∵底面NB1C1⊥侧面BB1C1C,∴C1N⊥侧面BB1C1C
∴截面C1NB⊥侧面BB1C1C
∴截面MBC1⊥侧面BB1C1C.
(3)解:结论是肯定的,充分性已由(2)证明,下面证必要性.
过M作ME⊥BC1于E,∵截面MBC1⊥侧面BB1C1C
∴ME⊥侧面BB1C1C,又∵AD⊥侧面BB1C1C.
∴ME∥AD,∴M、E、D、A共面
∵AM∥侧面BB1C1C,∴AM∥DE
∵CC1⊥AM,∴DE∥CC1
∵D是BC的中点,∴E是BC1的中点
∴AM=DE=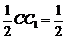 AA1,∴AM=MA1.
AA1,∴AM=MA1.
课堂小结:垂直和平行涉及题目的解决方法须熟练掌握两类相互转化关系:
1.平行转化

2.垂直转化

每一垂直或平行的判定就是从某一垂直或平行开始转向另一垂直或平行最终达到目的.
例如:有两个平面垂直时,一般要用性质定理,在一个平面内作交线的垂线,使之转化为线面垂直,然后进一步转化为线线垂直.