
2005年高考大纲数学学科的主体内容没有变化,与去年的考纲相比:
在能力要求部分比去年增加了对“四能力、一创新”的界定,比如究竟什么是运算能力等,过去的大纲未做过详细表述.考纲指出“运算能力是思维能力和运算技能的结合,运算包括对数字的计算、估值和近似的计算,对式子的组合变形与分解变形,对几何图形各几何量的计算求解等等.运算能力包括分析运算条件、探究运算方向、选择运算公式、确定运算程序等一系列过程中的思维能力,也包括在实施运算过程中遇到障碍而调整运算的能力”. 中心思想是要求考生能够“在运算当中,寻找解题的方法”,加大了对学生运算能力考查的要求.
在考试内容部分比去年删减了两处知识点:“能利用计算器解决解三角形的计算问题”,以及“了解多面体的欧拉公式”;在考试要求部分也有不少细微的变动,比如对“三垂线定理及其逆定理”的考查,由“了解”改成了“掌握”, 增加了“理解直线的倾斜角的概念”等等.《函数》这一章调整了一个知识点,把“函数的奇偶性”从下一章《三角函数》调了过来;改动了一个知识点,把“函数的应用举例”改成了“函数的应用”;增加了“了解函数的奇偶性的概念,掌握判断一些简单函数的奇偶性的方法” 的考试要求,对函数的意义、性质及综合应用的考查要求有了明显的提高.
在试卷结构部分第一次取消了选择题、填空题、解答题三种题型分值比例的限制,删去了容易题、中等题和难题的比例和这三类难度题的界定.而去年明确给出了“选择题40%、填空题10%、解答题50%”、“难度在0.7以上的是容易题,难度在0.4~0.7的试题为中等题,难度在0.4以下的为难题.三种试题的难度的比为3:5:2” ,这一改变为命题者对试卷难度的控制提供了较大的空间.这里还需要留意的是,考纲指出“试卷由容易题、中等题和难题组成,总体难度适当,并以中等题为主”, 去掉了去年 “以容易题和中档题为主”这句话中“容易题”这3个字,试卷整体难度预计会有所提高.
纵观近几年的新课程高考卷以及2004、2003年的江苏卷,函数的主干知识、知识的综合应用以及函数与方程思想等数学思想方法的考查,一直是高考的重点内容之一.在高考试卷上,与函数相关的试题所占比例始终在20%左右,且试题中既有灵活多变的客观性试题,又有一定能力要求的主观性试题.
(2004年,江苏卷8)若函数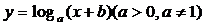 的图象过两点
的图象过两点
(-1,0)和(0,1),则
(A)a=2,b=2 (B)a=,b=2 (C)a=2,b=1 (D)a=,b=
(2003年,江苏卷6)函数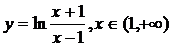 的反函数为
的反函数为
(A)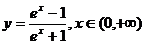 (B)
(B)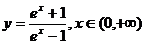
(C)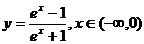 (D)
(D)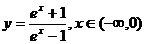
(2004年,江苏卷11)设k>1,f(x)=k(x-1)(x∈R) . 在平面直角坐标系xOy中,函数y=f(x)的图象与x轴交于A 点,它的反函数y=f -1(x)的图象与y轴交于B点,并且这两个函数的图象交于P点. 已知四边形OAPB的面积是3,则k等于
(A)3 (B) (C) (D)
(2003年,江苏卷9)已知方程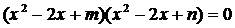 的四个根组成一个首项为
的四个根组成一个首项为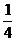 的等差数列,则
|m-n|=
的等差数列,则
|m-n|=
(A)1 (B)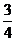 (C)
(C) (D)
(D)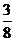
(2004年,江苏卷13)二次函数y=ax2+bx+c(x∈R)的部分对应值如下表:
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
y |
6 |
0 |
-4 |
-6 |
-6 |
-4 |
0 |
6 |
则不等式ax2+bx+c>0的解集是_______________________.
(2003年,江苏卷4)设函数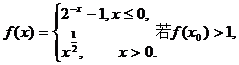 则x0的取值范围是
则x0的取值范围是
(A)(-1,1) (B)(-1,+∞)
(C)(-∞,-2)∪(0,+∞) (D)(-∞,-1)∪(1,+∞)
(2004年,江苏卷12)设函数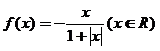 ,区间M=[a,b](a<b),集合N={
,区间M=[a,b](a<b),集合N={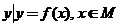 },则使M=N成立的实数对(a,b)有
},则使M=N成立的实数对(a,b)有
(A)0个 (B)1个 (C)2个 (D)无数多个
(2003年,江苏卷1)如果函数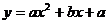 的图象与x轴有两个交点,则点(a,b)在aOb平面上的区域(不包含边界)为
的图象与x轴有两个交点,则点(a,b)在aOb平面上的区域(不包含边界)为

(2004年,江苏卷22)已知函数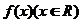 满足下列条件:对任意的实数x1,x2都有
满足下列条件:对任意的实数x1,x2都有 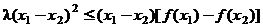
和 ,其中
,其中 是大于0的常数.
是大于0的常数.
设实数a0,a,b满足 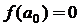 和
和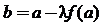
(Ⅰ)证明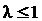 ,并且不存在
,并且不存在 ,使得
,使得 ;
;
(Ⅱ)证明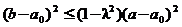 ;
;
(Ⅲ)证明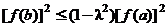 .
.
(2003年,江苏卷22) 设 如图,已知直线
如图,已知直线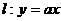 及曲线C:
及曲线C: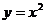 ,C上的点Q1的横坐标为
,C上的点Q1的横坐标为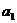 (
(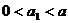 ).从C上的点Qn(n≥1)作直线平行于x轴,交直线
).从C上的点Qn(n≥1)作直线平行于x轴,交直线 于点
于点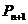 ,再从点
,再从点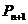 作直线平行于y轴,交曲线C于点Qn+1.
作直线平行于y轴,交曲线C于点Qn+1.
Qn (n=1,2,3,…)的横坐标构成数列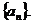
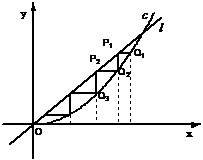 (Ⅰ)试求
(Ⅰ)试求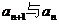 的关系,并求
的关系,并求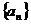 的通项公式;
的通项公式;
(Ⅱ)当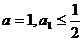 时,证明
时,证明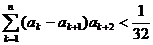 ;
;
(Ⅲ)当a=1时,证明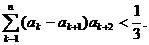
由于函数在高中数学中具有举足轻重的地位,它仍将是2005年高考的一个热点.对函数试题的设计依然会围绕几个基本初等函数和函数的性质、图像、应用考查函数知识;与方程、不等式、解几等内容相结合,考查函数知识的综合应用;在函数知识考查的同时,加强对函数方程、分类讨论、数形结合、等价转化等数学思想方法的考查.
1. 函数的奇偶性. 因为函数的奇偶性蕴涵着对称、变换、化归等丰富的数学知识和方法,今年考纲中新增加了“掌握判断一些简单函数的奇偶性的方法”这一考试要求,故而与函数的奇偶性有关的函数性质综合题应予以足够的关注.
例1.设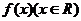 为奇函数,
为奇函数, 则
则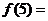
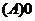
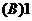
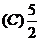
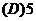
例2.已知定义域为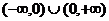 的函数
的函数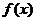 是偶函数,并且在
是偶函数,并且在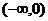 上是增函数,若
上是增函数,若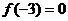 ,则
,则 的解集是
的解集是
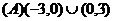

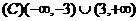
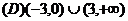
例3.函数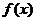 的定义域为
的定义域为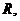 且
且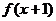 为奇函数,当
为奇函数,当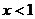 时,
时,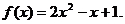 则当
则当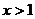 时,
时,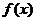 的单调减区间为
的单调减区间为
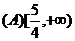
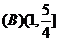
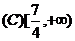
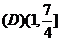
例4. 已知函数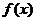 是奇函数,当
是奇函数,当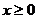 时,
时, ,设
,设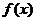 的反函数是
的反函数是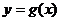 ,则
,则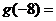
例5.如果函数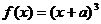 对任意实数
对任意实数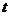 ,都有
,都有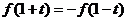 ,则
,则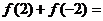
2.复合函数. 函数试题的设计始终围绕着几个基本初等函数,并通过这几个函数之间的串联、组合成为复合函数,达到对函数知识、方法和思想的深刻考查.因而对复合函数类问题,要掌握换元、分解、整体代入等方法,找到其母函数,从而化归为基本初等函数问题加以解决.
例6.若 ,要使
,要使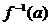 有意义,实数
有意义,实数 的取值范围是
的取值范围是
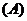

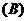
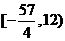
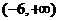
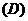
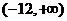
例7.若函数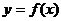 的图象可由函数
的图象可由函数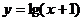 的图象绕坐标原点
的图象绕坐标原点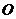 逆时针旋转
逆时针旋转 得到,则
得到,则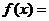
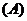
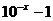
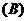
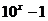
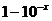
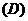
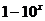
例8.已知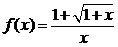 ,
, 、
、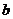 为两个不相等的正实数,则下列不等式正确的是
为两个不相等的正实数,则下列不等式正确的是
(A) (B)
(B)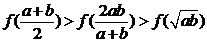
(C)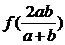

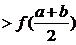 (D)
(D)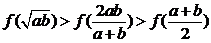
例9.已知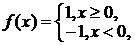 则不等式
则不等式 ≤5的解集是
.
≤5的解集是
.
例10.已知函数 ,有下列命题:①
,有下列命题:①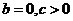 时,
时, 只有一个实数根②
只有一个实数根②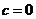 时,
时,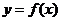 是奇函数③
是奇函数③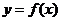 的图象关于点
的图象关于点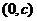 对称④方程
对称④方程 至多有3个实数根,则正确的命题的序号为
至多有3个实数根,则正确的命题的序号为
3.抽象函数.抽象函数问题是近几年高考中函数类问题的一个新的热点,由于具体函数与抽象函数之间是特殊化与一般化的关系,因而抽象函数问题的解决方法更加灵活多样,既可以采用特殊化方法,又可以回归函数的各种性质,有利于考查学生的抽象思维能力,故而应引起我们的高度重视.
例11.已知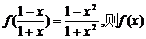 的解析式可取为
的解析式可取为
(A)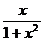 (B)
(B)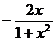 (C)
(C)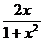 (D)
(D)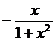
例12. 若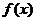 和g(x)都是定义在实数集R上的函数,且方程
和g(x)都是定义在实数集R上的函数,且方程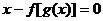 有实数解,则
有实数解,则 不可能是
不可能是
(A)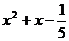 (B)
(B)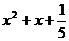 (C)
(C)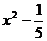 (D)
(D)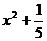
例13.给出四个函数,分别满足:
①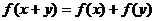 ②
②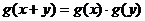
③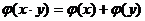 ④
④ 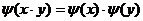

又给出四个函数的图像,则正确的匹配方案是
(A)①-a ②-b ③-c ④-d (B)①-b ②-c ③-a ④-d
(C)①-c ②-a ③-b ④-d (D)①-d ②-a ③-b ④-c
例14.已知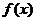 的定义域为
的定义域为 ,若
,若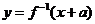 与
与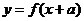 互为反函数且
互为反函数且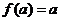 (
( 为非零常数),则
为非零常数),则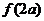 =
=
例15. 函数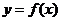 的定义域为
的定义域为 ,对于任意实数
,对于任意实数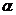 、
、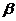 ,有:
,有:
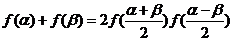 且
且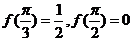
(1)求证: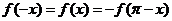
(2)若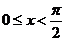 ,
,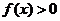 ,证明:
,证明: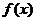 在
在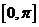 递减
递减
4.数学思想.数学思想能从整体上深层次认识数学的实质,对数学知识、数学方法的运用起到导向作用.对数学思想的教学在新授课和第一轮复习中通常处在“隐含、渗透”阶段,在第二轮复习中就应提升到“介绍、运用”阶段,应更加明确,更加系统,这是一个从模糊到清晰的质的飞跃。函数一章包含了考纲中明确考查的四种数学思想方法,即函数方程思想、分类讨论思想、数形结合思想和等价转化思想等,我们应努力使其成为学生解决函数问题的自觉的行动指南.
例16. 若方程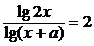 无解,则
无解,则
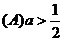


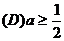
例17. 定义在R上的奇函数 为任意正实数,且
为任意正实数,且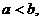 若
若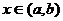 时,恒有
时,恒有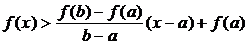 成立,则下列关系式中正确的是
成立,则下列关系式中正确的是
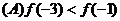
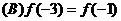
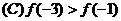
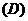 以上都不正确
以上都不正确
例18. 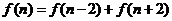 对一切大于1的正整数
对一切大于1的正整数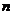 都成立,
都成立, 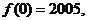 则
则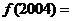
例19.实数 满足:
满足: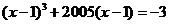 ,
,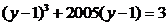 ,
,
则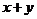 =
=
例20. 已知 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.
(1)求实数 的值组成的集合A;
的值组成的集合A;
(2)设关于x的方程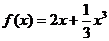 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式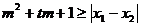 对任意
对任意 及
及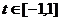 恒成立?若存在,求m的取值范围;若不存在,请说明理由.
恒成立?若存在,求m的取值范围;若不存在,请说明理由.
通过对近几年的新课程高考卷以及2004、2003年的江苏卷中函数类试题的研究,特提出复习建议如下:
1、重视对函数图像和性质的再现.要引导学生回归基础,多问问自己:函数的性质主要有哪些?具体的函数(二次函数、指数函数、对数函数、三角函数等)又有哪些性质呢?这些基本初等函数的图像清楚吗?图像的变换(平移、对称等)方法都掌握了吗?等等.
2.重视函数定义域在解决函数性质时的作用.在讨论函数的奇偶性、单调性时,在求函数的值域或最值时,在求函数的解析式或变形时,都不能丢掉函数的灵魂“定义域”.有些问题中定义域比较隐蔽,要引导学生学会认真审题,把隐含条件挖掘出来,在解有关函数应用题时还要结合实际意义去考虑.
3.解答函数类客观型试题时,要重视数形结合思想方法的应用.应用数形结合思想,就是充分考察问题的条件和结论之间的内在联系,即分析其代数意义又揭示其几何意义,借助于函数的图像,就可以直观地、快速地寻找解题思路,使问题得到解决.这就要求学生能熟练地掌握基本初等函数的图像特征.
4.重视函数与导数的结合.利用导数判定一些函数的单调性、求函数的极值和最值,这是研究函数性质的强有力的工具,并且具有普遍的适用性,也是新课程高考卷的一个热点内容.这就要求我们在复习中高度重视,尤其要加强对三次函数性质的探讨,因为三次函数求导后又与传统的重点内容二次函数相互联系.