
1.考试内容
(1)分类计数原理与分步计数原理,排列与组合.
(2)等可能性事件的概率,互斥事件有一个发生的概率,相互独立事件同时发生的概率.
2.考试要求
(1)掌握分类计数原理与分步计数原理,并能用它们分析和解决一些简单的应用问题.
(2)理解排列与组合的意义,掌握排列数与组合数的计算公式,掌握组合数的两个性质,并能用它们解决一些简单的应用问题.
(3)了解等可能性事件的概率的意义,会用排列组合公式计算一些等可能性事件的概率.
(4)了解互斥事件的意义,会用互斥事件的概率加法公式计算一些事件的概率.
(5)了解相互独立事件的意义,会用相互独立事件的概率乘法公式计算一些事件的概率,会计算事件在n次独立重复试验中恰好发生k次的概率.
排列与组合、概率与统计是高中数学的重要内容.一方面,这部分内容占用教学时数多达36课时,另一方面,这部分内容是进一步学习高等数学的基础知识,因此,它是高考数学命题的重要内容.从近三年全国高考数学(新材)试题来看,主要是考查排列与组合、概率与统计的基本概念、公式及基本技能、方法,以及分析问题和解决问题的能力.试题特点是基础和全面.题目类型有选择题、填空题、解答题,一般是两小(9分-10分)一大(12分),解答题通常是概率问题.试题难度多为低中档.为了支持高中数学课程的改革,高考数学命题对这部分将进一步重视,但题目数量、难度、题型将会保持稳定.
例1.(1999年全国)在一块并排10垄的田地中,选择2垄分别种植A、B两种作物,每种作物种植一垄,为有利于作物生长,要求A、B两种作物间的间隔不小于6垄,则不同的选垄方法共有_______种(用数字作答).
[解析]
A种植在左边第一垄时,B有3种不同的种植方法;
A种植在左边第二垄时,B有两种不同的种植方法;
A种植在左边第三垄时,B只有一种种植方法.
B在左边种植的情形与上述情形相同.
故共有2(3+2+1)=12种不同的选垄方法.
∴ 应填12.
例2.(2003年新教材)将3种作物种植在如图所示的5块试验田里,每一块种植一种作物且相邻的试验田不能种植同一作物,不同的种植方法共有______种(以数字作答).

[解析]
将5块试验田从左到右依次看作甲、乙、丙、丁、戊,3种作物依次看作A、B、C,则3种作物都可以种植在甲试验田里,由于相邻的试验田不能种植同一种作物,从而可知在乙试验田里只能有两种作物.同理,在丙、丁、戊试验田里也只能有两种作物可以种植.
由分步计数原理,不同的种植方法共有3×2×2×2=48种.
∴应填:48
 例3.(2003年全国高考题)某城市中心广场建造一个花圃,花圃分为6个部分(如图),现要栽种4种不同颜色的花,每部分栽种1种且相邻部分不能栽种同样颜色的花,不同的栽法有_______种.
例3.(2003年全国高考题)某城市中心广场建造一个花圃,花圃分为6个部分(如图),现要栽种4种不同颜色的花,每部分栽种1种且相邻部分不能栽种同样颜色的花,不同的栽法有_______种.
[解析]
由于第1、2、3块两两相邻,我们先安排这三块,给第1、2、3块种花时分别有4、3、2种种法,所以共有4×3×2=24种不同种法.
下面给第4块种花,若第4块与第6块同色,只有一种种植方法,则第5块只有2种种法,若第4块与第2块同色时,共有2×1=2种种法.
若第4块与第6块不同色,但第4块与第2块同色,则第6块有2种种植的方案,而第5块只有1种种法,共有2种不同的种植方法.
若第4块与第6块不同色,但第4块与第2块不同色,则第6块有1种种法,则第5块也有一种不同种法,所以第4块与第6块不同色时,有1种种法.
综上共有24×(2+2+1)=120种不同的种植方法.
例4.(2003年春季考试题)某班新年联欢会原定的5个节目已排成节目单,开演前又增加了两个新节目,如果将这两个节目插入原节目单中,那么不同的插法的种数为
A、42 B、30 C、20 D、12
[解析]
将两个新节目插入5个固定顺序节目单有两种情况:
(1)两个新节目相邻的插法种数为 ;
;
(2)两个节目不相邻的插法种数为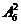 ;由分类计数原理共有
;由分类计数原理共有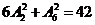 种方法,选A.
种方法,选A.
例5.(2004重庆)(本小题满分12分)
设甲、已、丙三人每次射击命中目标的概率分别为0.7、0.6和0.5。
(1)三人各向目标射击一次,求至少有一人命中目标的概率及恰有两人命中目标的概率;
(2)若甲单独向目标射击三次,求他恰好命中两次的概率.
解:(I)设AK表示“第k人命中目标”,k=1,2,3.
这里,A1,A2,A3独立,且P(A1)=0.7,P(A2)=0.6,P(A3)=0.5.
从而,至少有一人命中目标的概率为
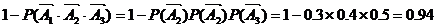
恰有两人命中目标的概率为

答:至少有一人命中目标的概率为0.94,恰有两人命中目标的概率为0.44
(II)设甲每次射击为一次试验,从而该问题构成三次重复独立试验.又已知在每次试验中事件“命中目标”发生的概率为0.7,故所求概率为
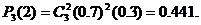
答:他恰好命中两次的概率为0.441.
例6.(2002年理科高考题)某单位6个员工借助互联网开展工作,每个员工上网的概率都是0.5(相互独立).
(Ⅰ)求至少3人同时上网的概率;
(Ⅱ)至少几人同时上网的概率小于0.3 ?
分析: (Ⅰ)至少3人同时上网的概率等于1减去至多2人同时上网的概率.即

(Ⅱ)至少4人同时上网的概率为:
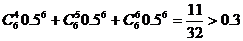
.至少5人同时上网的概率为:
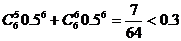
因此, 至少5人同时上网的概率小于0.3.
思路:如果在1次试验中某事件发生的概率是P,那么在n次独立重复试验中这个事件恰好发生K次的概率为 .
.
例7.(2004湖南)(本小题满分12分)
甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为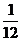 ,甲、丙两台机床加工的零件都是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为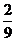 .
.
(Ⅰ)分别求甲、乙、丙三台机床各自加工零件是一等品的概率;
(Ⅱ)从甲、乙、丙加工的零件中各取一个检验,求至少有一个一等品的概率.
解:(Ⅰ)设A、B、C分别为甲、乙、丙三台机床各自加工的零件是一等品的事件.
|
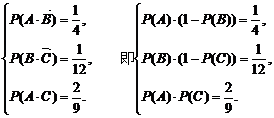
由①、③得 代入②得 27[P(C)]2-51P(C)+22=0.
代入②得 27[P(C)]2-51P(C)+22=0.
解得  (舍去).
(舍去).
将  分别代入 ③、② 可得
分别代入 ③、② 可得 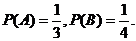
即甲、乙、丙三台机床各加工的零件是一等品的概率分别是
(Ⅱ)记D为从甲、乙、丙加工的零件中各取一个检验,至少有一个一等品的事件,
则 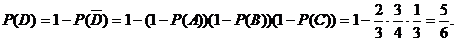
故从甲、乙、丙加工的零件中各取一个检验,至少有一个一等品的概率为
概率和统计是一门专门“研究偶然现象统计规律性”的学科。有着广泛的应用背景。近几年来新课程卷高考试卷也把概率统计的基本知识和方法:随机事件、等可能事件、互斥事件、相互独立事件、独立重复实验等概念及相应的计算等列为考察的重点,作为必考内容。
1. 概率的定义:一般地,在大量重复进行同一实验时,事件A发生的频率m/n总是接近某个常数,在它附近摆动,这个常数叫事件A的概率。
2. 等可能事件的概率:P(A)=m/n.
3. 互斥事件:不可能同时发生的事件。互斥事件A,B中有一个发生的概率为:P(A+B)=P(A)+P(B)。特别地
4. 相互独立事件:如果一个事件是否发生对另一个事件发生的概率没有影响。独立事件A,B同时发生的概率:P(A•B)=P(A)•P(B)。
5. n次独立重复实验中事件A发生k次的概率: 。
。
复习这部分内容及解答此类问题首先必须使学生明确判断两点:(1)对于每个随机实验来说,所有可能出现的实验结果数n必须是有限个;(2)出现的所有不同的实验结果数m其可能性大小必须是相同的。只有在同时满足(1)、(2)的条件下,运用等可能事件的概率计算公式P(A)=m/n得出的结果才是正确的。而事件间得的“互相排斥”与“相互独立”是学生理解的一个难点,能否准确判断事件之间是否互相排斥或相互独立,正确理解“和事件”或“积事件”的意义,是考查的又一个重点,学生常因为混淆不清而导致计算错误。在同一实验中两事件的“互相排斥”是指两个事件不可能同时发生;两事件“相互独立”是指一个事件发生与否对另一个事件发生的概率没有影响。在实际运用中我们常常不是根据定义来判断事件的独立性,而是应用实验的方法,由实验的独立性去判断事件的独立性。而在应用题背景条件下,能否把一个复杂事件分解为若干个互相排斥或相互独立、既不重复又不遗漏的简单事件是解答这类应用题的关键,也是考查学生分析问题、解决问题的能力的重要环节。
例题1:某零件从毛坯到成品,一共要经过6道自动加工工序。如果各道工序出次品的概率依次为0.01、0.02、0.03、0.03、0.05、0.05,那么这种零件的次品率是多少?
错解:设第i道工序出次品的事件为Ai,i=1、2、…、6,Ai是互斥事件,则Ai中至少有一个事件发生就为次品,故这种零件的次品率为P(A1+A2+…+A6)=P(A1)+P(A2)+…+P(A6)=0.19。
分析:错误原因是将相互独立的事件看成互斥事件。由题意可知,只有同时经过6道工序才能将事件完成,不能只考虑一道工序是否通过。
设第i道工序出现次品的事件记为Ai,i=1、2、…、6,它们相互独立但不互斥,则Ai中至少有一个事件发生就出现次品,所以该种零件的次品率为P(A1+A2+…+A6)
=1-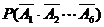

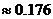 。
。
又如:某家庭电话在家中有人时,打进的电话响第1声时被接的概率为0.1,响第2声时被接的概率为0.3,响第3声时被接的概率为0.4,响第4声时被接的概率为0.1。那么该电话在前4声内被接的概率是多少?
例题2、从原点出发的某质点M,按照向量 移动的概率为2/3,按照向量
移动的概率为2/3,按照向量 移动的概率为1/3。设M可到达点(0,n)的概率为Pn。
移动的概率为1/3。设M可到达点(0,n)的概率为Pn。
(1)求P1 ,P2;
(2)求证: ;
;
(3)求Pn的表达式。
解析:(1)点M到达点(0,1)的概率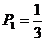 ,点M到达点(0,2)的事件由两个互斥的事件组成:①“点M先按向量
,点M到达点(0,2)的事件由两个互斥的事件组成:①“点M先按向量 移动到达点(0,1),再按向量
移动到达点(0,1),再按向量 平移到达点(0,2)”,此时概率为
平移到达点(0,2)”,此时概率为 ;②“点M按向量
;②“点M按向量 移动直接到达(0,2)”,此时的概率为
移动直接到达(0,2)”,此时的概率为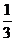 。于是所求的概率为:
。于是所求的概率为:
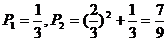 。
。
(2)M点到达(0,n+2)由两个互斥的事件组成:①“从点(0,n+1)按向量 移动”,此时概率为
移动”,此时概率为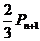 ;②“从点(0,n)按向量
;②“从点(0,n)按向量 移动”此时概率为
移动”此时概率为 。于是
。于是 ,即
,即 。
。
(3)由(2)可知,数列{Pn+2-Pn+1}是以P2-P1=1/9为首项,公比为-1/3的等比数列,即 ,故
,故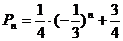 。
。
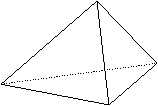
例题3、设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的。现投掷骰子根据其点数决定棋子是否移动:若投出的点数是奇数,则棋子不动;若投出的点数是偶数,棋子移动到另一个顶点。若棋子的初始位置在顶点A,回答下列问题。
(1)投了2次骰子,棋子才到达顶点B的概率是多少?
(2)投了3次骰子,棋子恰好在顶点B的概率是多少?
分析:棋子从顶点A移动到顶点B,C,D的概率都是1/6,而不移动的概率是3/6=1/2。
 (1)分两种情形:①第一次不动,第二次移到B,即
(1)分两种情形:①第一次不动,第二次移到B,即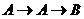 ;②两次都动,即
;②两次都动,即
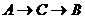 或
或 ,故投了2次骰子,棋子才到达顶点B的概率为
,故投了2次骰子,棋子才到达顶点B的概率为
 。
。
(2)①两次停在相同顶点: 、
、
 、
、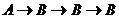 ;②一次停在相同顶点:
;②一次停在相同顶点: 、
、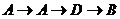 、
、 、
、 、
、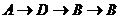 、
、 ;③每次都向其它顶点移动:
;③每次都向其它顶点移动: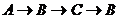 、
、
 、
、 、
、 、
、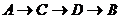 、
、 、
、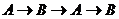 。故投3次骰子,棋子恰好在顶点B的概率是
。故投3次骰子,棋子恰好在顶点B的概率是 。
。
1.(2004辽宁)有两排座位,前排11个座位,后排12个座位,现安排2人就座,规定前排中间的3个座位不能坐,并且这2人不左右相邻,那么不同排法的种数是 ( )
A.234 B.346 C.350 D.363
2.(2004湖南)从正方体的八个顶点中任取三个点为顶点作三角形,其中直角三角形的个数为 A.56 B.52 C.48 D.40 ( )
3.(2002全国理)从正方体的6个面中选取3个面,其中有2个面不相邻的选法共有( )
A.8种 B.12种 C.16种 D.20种
4.(2004福建)某校高二年级共有六个班级,现从外地转入4名学生,要安排到该年级的两个班级且每班安排2名,则不同的安排方案种数为 ( )
A.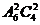 B.
B.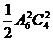 C.
C. D.
D.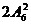
5.(2002全国春招)从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同工作.若其中甲、乙两名支援者都不能从事翻译工作,则选派方案共有 ( )
(A)280种 (B)240种 (C)180种 (D)96种
6.(2004广东)一台X型号自动机床在一小时内不需要工人照看的概率为0.8000,有四台这中型号的自动机床各自独立工作,则在一小时内至多2台机床需要工人照看的概率是
A.0.1536 B. 0.1808 C. 0.5632 D. 0.9728 ( )
7.(2004江苏)将一颗质地均匀的骰子(它是一种各面上分别标有点数1,2,3,4,5,6的正方体玩具)先后抛掷3次,至少出现一次6点向上的概率是 ( )
A. B. C. D.
8.(2004辽宁)甲、乙两人独立地解同一问题,甲解决这个问题的概率是p1,乙解决这个问题的概率是p2,那么恰好有1人解决这个问题的概率是 ( )
A. B.
B. C.
C. D.
D.
9.(2004重庆)已知盒中装有3只螺口与7只卡口灯炮,这些灯炮的外形与功率都相同且灯口向下放着,现需要一只卡口灯炮使用,电工师傅每次从中任取一只并不放回,则他直到第3次才取得卡口灯炮的概率为 ( )
A. B.
B. C.
C.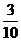 D.
D.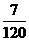
10.(2004北京)从长度分别为1,2,3,4,5的五条线段中,任取三条的不同取法共有n种。在这些取法中,以取出的三条线段为边可组成的钝角三角形的个数为m,则 等于 ( )
等于 ( )
A. B.
B.  C.
C.  D.
D. 
11.(2004湖北)将标号为1,2,…,10的10个球放入标号为1,2,…,10的10个盒子内,每个盒内放一个球,则恰好有3个球的标号与其所在盒子的标号不一致的放入方法共
有 种.(以数字作答)
12.(2000广东)乒乓球队的10名队员中有3名主力队员,派5名参加比赛。3名主力队 员要安排在第一、三、五位置,其余7名队员选2名安排在第二、四
位置,那么不同的出场安排共有_ __种(用数字作答)。
13. (2003广东省)如图,一个地区分为5个行政区域,
(2003广东省)如图,一个地区分为5个行政区域,
现给地图着色,要求相邻区域不得
使用同一颜色,现有4种颜色可
供选择,则不同的着色方法共有
种.(以数字作答)
14.(2004广东)某班委会由4名男生与3名女生组成,现从中选出2人担任正副班长,其中至少有1名女生当选的概率是 (用分数作答)
15.(2004辽宁)口袋内装有10个相同的球,其中5个球标有数字0,5个球标有数字1,若从袋中摸出5个球,那么摸出的5个球所标数字之和小于2或大于3的概率是 .
16.(2004上海文科)若在二项式(x+1)10的展开式中任取一项,则该项的系数为奇数的概率是 . (结果用分数表示)
17.(2000江西、天津)从含有500个个体的总体中一次性地抽取25个个体,假定其中每个个体被抽到的概率相等,那么总体中的每个个体被抽取的概率等于 。
18.(2001上海春招)在大小相同的6个球中,2个红球,4个是白球.若从中任意选取3 个,则所选的3个球中至少有1个红球的概率是___ ___.(结果用分数表示)
19.(2004福建)某射手射击1次,击中目标的概率是0.9.他连续射击4次,且各次射击是否击中目标相互之间没有影响.有下列结论:
①他第3次击中目标的概率是0.9;②他恰好击中目标3次的概率是0.93×0.1;
③他至少击中目标1次的概率是1-0.14.
其中正确结论的序号是 (写出所有正确结论的序号).
20.(2003年全国)有三种产品,合格率分别是0.90,0.95和0.95.各抽取一件进行检验。
(Ⅰ)求恰有一件不合格的概率;
(Ⅱ)求至少有两件不合格的概率。(精确到0.001)
附录:考前热身答案
11.240 ;12.252 ;13.72 ;14. ;15.
;15.
16. ; 17.0.05 ; 18.
; 17.0.05 ; 18.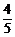 ;19.
①③
;19.
①③
20.分析:设抽到合格产品的事件分别为A,B,C,则
P(A)=0.90 P(B)=P(C)=0.95
P( )=0.10 P(
)=0.10 P( )=P(
)=P( )=0.05
)=0.05
(Ⅰ)因为A,B,C相互独立,故恰有一件不合格的概率为:
P(A.B. )+_P(A.
)+_P(A. .C)+P(
.C)+P( .B.C)
.B.C)
=P(A).P(B).P( )+P(A).P(
)+P(A).P( ).P(C)+P(
).P(C)+P( ).P(B).P(C)
).P(B).P(C)
=0.90×0.95×0.05+0.90×0.05×0.95+0.10×0.95×o.95
=0.176
(Ⅱ)至少有两件不合格的概率为:
P(A. .
. )+P(
)+P( .B.
.B. )+P(
)+P( .
. .C)+P(
.C)+P( .
. .
. )
)
=0.90×0.05×0.05+0.10×0.95×0.05+0.10×0.05×0.95+0.10×0.05×0.05
=0.012
思路:1.正确分清互斥事件与相互独立事件是解决此类问题的关键.
2.只有当事件A,B互斥时,才能运用公式P(A+B)=P(A)+P(B);只有当事件A,B相互独立时,才能运用公式P(A.B)=P(A).P(B).