1.不等式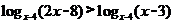 的解集是(
)
的解集是(
)
(A)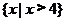 (B)
(B)
(C)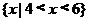 (D)
(D)
2.不等式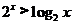 的解集是(
)
的解集是(
)
(A)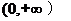 (B)
(B)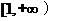 (C)R (D)ф
(C)R (D)ф
3.不等式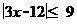 的整数解的个数是(
)
的整数解的个数是(
)
(A)7 (B)6 (C)5 (D)4
4.设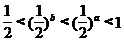 ,则(
)
,则(
)
(A)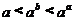 (B)
(B)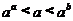 (C)
(C)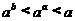 (D)
(D)
5.若实数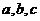 满足
满足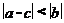 ,则下列不等式中成立的是(
)
,则下列不等式中成立的是(
)
(A)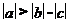 (B)
(B)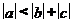 (C)
(C)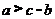 (D)
(D)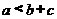
6.若不等式 成立的充分条件是
成立的充分条件是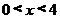 ,则
,则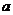 的取值范围是(
)
的取值范围是(
)
(A)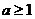 (B)
(B)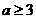 (C)
(C)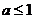 (D)
(D)
7.若关于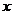 的不等式
的不等式 在R上恒成立,则
在R上恒成立,则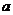 的最大值是(
)
的最大值是(
)
(A)0 (B)1 (C)-1 (D)2
8.设 、
、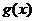 都是定义在
都是定义在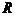 上的奇函数,不等式
上的奇函数,不等式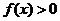 的解集为
的解集为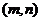 ,不等式
,不等式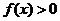 的解集为
的解集为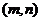 ,不等式
,不等式 的解集为
的解集为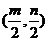 ,其中
,其中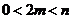 ,则不等式
,则不等式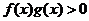 的解集为(
)
的解集为(
)
(A) 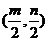 (B)
(B)
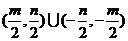
(C) 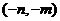 (D)
(D)

9.若奇函数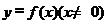 。当
。当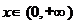 时,
时, ,则不等式
,则不等式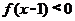 的解集是(
)
的解集是(
)
(A)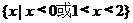 (B)
(B)
(C)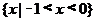 (D)
(D)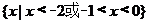
10.若关于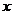 的方程
的方程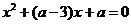 的两根均为正数,则实数
的两根均为正数,则实数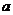 的范围是(
)
的范围是(
)
(A)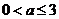 (B)
(B) 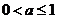 (C)
(C) (D)
(D)
 或
或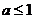
11.已知 ,则下列不等式中正确的是(
)
,则下列不等式中正确的是(
)
(A) (B)
(B)
(C)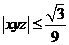 (D)
(D)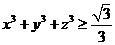
12.定义在R上的奇函数 为减函数,设
为减函数,设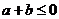 ,给出下列不等式:
,给出下列不等式:
①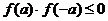 ②
②
③ ④
④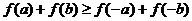
其中正确的不等式序号是( )
(A) ①②④ (B) ①④ (C) ②④ (D) ①③
13、若对实数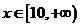 恒有
恒有 ,则实数m的取值范围是___________。
,则实数m的取值范围是___________。
14、不等式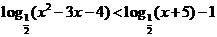 的解集是______________________。
的解集是______________________。
15、已知一个不等式①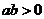 ,②
,② ,③
,③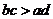 ,以其中的两个作条件,余下的一个作结论,则可组成_______________个正确命题。
,以其中的两个作条件,余下的一个作结论,则可组成_______________个正确命题。
16、直角 的三边为a、b、c,且c>b>a,设
的三边为a、b、c,且c>b>a,设 、
、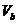 、
、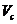 分别表示以a、b、c为轴旋转所成旋转体的体积,则
分别表示以a、b、c为轴旋转所成旋转体的体积,则 、
、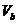 、
、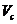 之间的大小关系是____________________。
之间的大小关系是____________________。
17.解不等式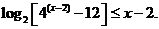
18.解关于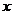 的不等式
的不等式
19.已知不等式 的解集为A,不等式
的解集为A,不等式 的解集为B,且
的解集为B,且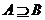 ,求实数
,求实数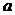 的取值范围。
的取值范围。
2005年 专题复习三 不等式及其应用 [高考要点] 1. 系统地掌握不等式的性质; 2. 掌握不等式证明的常用方法; 3. 掌握均值不等式:及其在求最值方面的用途(注意“正、定、等”三个条件的内涵)。 4. 掌握整式不等式、分式不等式、无理不等式、指数不等式和对数不等式的解法。 5. 掌握含绝对值不等式的基本性质,会解含绝对值的不等式。 [例题选讲] [例1] 已知,解关于的等式 [例2] 已知函数 (1)当时,解不等式; (2)如果对满足的一切实数,都有,求的取值范围。参考答案
(参考答案)1~12、DAAAB
BBDAB CB 13、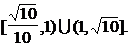 14、
14、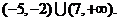 15、3个.
16、
15、3个.
16、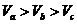
17、
18、 或
或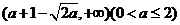
19、