
《排列、组合、二项式定理和概率》
1、排列数、组合数的计算、化简、证明等;会解排列、组合应用题,掌握常见应用题的处理思路。
2、掌握二项式定理,会用展开式通项求有关展开式的问题。
3、理解随机事件的概率,会求等可能事件的概率,能用加法公式和乘法公式求互斥事件和相互独立事件同时发生的概率。
1、分类计数原理和分步计数原理是排列组合的基础和核心,既可用来推导排列数、组合数公式,也可用来直接解题。它们的共同点都是把一个事件分成若干个分事件来进行计算。只不过利用分类计算原理时,每一种方法都可能独立完成事件;如需连续若干步才能完成的则是分步。利用分类计数原理,重在分“类”,类与类之间具有独立性和并列性;利用分步计数原理,重在分步;步与步之间具有相依性和连续性。比较复杂的问题,常先分类再分步。
2、排列数与组合数都是计算完成事件方法个数的公式,排列数是研究排列(既取又排)个数的公式,组合数是研究组合(只取不排)个数的公式,是否有序是它们之间的本质区别。
排列数公式: ,当m=n时,
,当m=n时,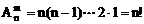 ,其中m,n∈N+,m≤n,规定0!=1
,其中m,n∈N+,m≤n,规定0!=1
组合数公式: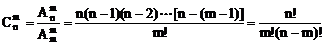
组合数性质: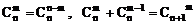 ,规定
,规定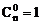 ,其中m,n∈N+,m≤n
,其中m,n∈N+,m≤n
3、处理排列组合应用题的规律
(1)两种思路:直接法,间接法
(2)两种途径:元素分析法,位置分析法
(3)对排列组合的混合题,一般先选再排,即先组合再排列。弄清要完成什么样的事件是前提
(4)基本题型及方法:捆绑法,插空法,错位法,分组分配法,均匀分组法,逆向思考法等
4、二项式定理
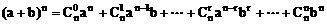
通项公式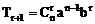 ,r=0,1,2,…,n
,r=0,1,2,…,n
二项式系数的性质:
(1)对称性,在展开式中,与首末两端“等距离”的两个二项式系数相等,即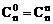 ,
,
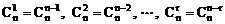 ;
;
(2)增减性与最大值:在二项式展开式中,二项式系数先增后减,且在中间取得最大值,当n是偶数时,中间一项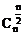 最大;当n是奇数时,中间两项
最大;当n是奇数时,中间两项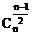 ,
,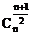 相等,且为最大值;
相等,且为最大值;
(3)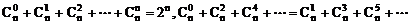
5、概率
(1)概率是频率的近似值,两者是不同概念
(2)等可能事件中概率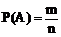 ,P(A)∈[0,1]
,P(A)∈[0,1]
(3)互斥事件A,B中有一个发生的概率:加法公式P(A+B)=P(A)+P(B)
特例: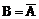 时,
时,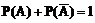 ,即对立事件的概率和为1
,即对立事件的概率和为1
(4)相互独立事件A,B同时发生的概率P(A.B)=P(A)P(B)
(5)事件A在n次独立重复试验中恰好发生k次的概率Pn(k)=CnkPk(1-P)n-k,其中P为事件A在一次试验中发生的概率,此式为二项式[(1-P)+P]n展开的第k+1项
例1、用n种不同颜色为下列两块广告牌着色(如图),要求在①,②,③,④个区域中相邻(有公共边界)的区域不用同一种颜色。
(1)若n=6,为甲着色时共有多少种不同方法?
(2)若为乙着色时共有120种不同方法,求n。
解:完成着色这件事,共分四个步骤,可依次考虑为①、②、③、④着色时各自的方法数,再由乘法原理确定决的着色方法数。因此
(1)为①着色有6种方法,为②着色有5种方法,为③着色有4种方法,为④着色也只有4种方法。
∴ 共有着色方法6×5×4×4=480种
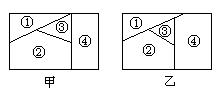 (2)与①的区别在于与④相邻的区域由两块变成了三块,同理,不同的着色方法数是n(n-1)(n-2)(n-3)
(2)与①的区别在于与④相邻的区域由两块变成了三块,同理,不同的着色方法数是n(n-1)(n-2)(n-3)
由n(n-1)(n-2)(n-3)=120
∴ (n2-3n)(n2-3n+2)-120=0
即(n2-3n)2+2(n2-3n)-12×10=0
∴ n2-3n-10=0
∴ n=5
例2、计算下列各题:
(1)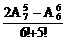
(2)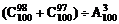
(3)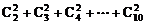
解:(1)原式=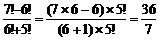
(2)原式=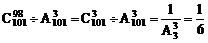
(3)原式=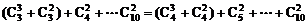
=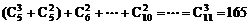
例3、按以下要求分配6本不同的书,各有几种分法?
(1)平均分给甲、乙、丙三人,每人2本;
(2)平均分成三份,每份2本;
(3)甲、乙、丙三人一人得1本,一人得2本,一人得3本;
(4)分成三份,一份1本,一份2本,一份3本;
(5)甲、乙、丙三人中,一人得4本,另二人每人得1本;
(6)分成三份,一份4本,另两份每份1本;
(7)甲得1本,乙得1本,丙得4本(均只要求列式)
解:(1)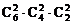 ;
;
(2)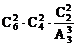
(3)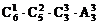
(4)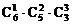
(5)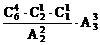
(6)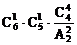
(7)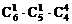
评注:有关排列组合混合题常常是先组合再排列。
例4、四面体的顶点和各棱中点共有10个点,在其中取4个不共面的点,不同的取法共有( )
A、150种 B、147种 C、144种 D、141种
解:从10个点中任取4个点有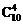 种取法,其中4点共面的情况有三类。第一类,取出的4个点位于四面体的同一个面内,有
种取法,其中4点共面的情况有三类。第一类,取出的4个点位于四面体的同一个面内,有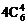 种;第二类,取任一条棱上的3个点及该棱对棱的中点,这4点共面,有6种;第三类,由中位线构成的平行四边形(其两组对边分别平行于四面体相对的两条棱),它的4个点共面,有3种。以上三种情况不合要求应减掉,所以不同的取法共有
种;第二类,取任一条棱上的3个点及该棱对棱的中点,这4点共面,有6种;第三类,由中位线构成的平行四边形(其两组对边分别平行于四面体相对的两条棱),它的4个点共面,有3种。以上三种情况不合要求应减掉,所以不同的取法共有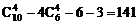 (种)
(种)
例5、求(4+2x+x2)(2-x)7的展开式中x5的系数。
解:(4+2x+x2)(2-x)7=(8-x3)(x-2)6
=(8-x3)[(x6-2C61x5+(-2)2C62x4+(-2)3C63x3+(-2)4C64x2+…]
∴ 含x5的项为-2×8×C61.x5-(-2)4C64x5=-336x5
∴ x5的系数为-336
例6、已知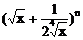 的展开式前三项中的x的系数成等差数列。
的展开式前三项中的x的系数成等差数列。
(1)求展开式里所有的x的有理项;
(2)求展开式里系数最大的项。
解:(1)∵
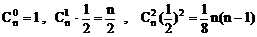
由题设可知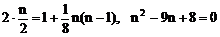
解得n=8或n=1(舍去)
当n=8时,通项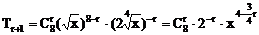
据题意, 必为整数,从而可知r必为4的倍数,而0≤r≤8
必为整数,从而可知r必为4的倍数,而0≤r≤8
∴ r=0,4,8,故x的有理项为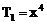 ,
,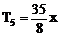 ,
,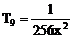
(3)设第r+1项的系数tr+1最大,显然tr+1>0,故有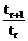 ≥1且
≥1且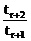 ≤1
≤1
∵ 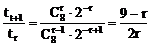
由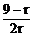 ≥1得r≤3
≥1得r≤3
又∵ 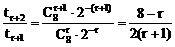
由 ≤1得:r≥2
≤1得:r≥2
∴ r=2或r=3所求项为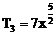 和
和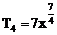
例7、设a>1,n∈N,且n≥2,求证: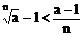
证明:设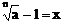 ,则(x+1)n=a
,则(x+1)n=a
欲证原不等式,即证nx<(x+1)n-1,其中x>0
∵ 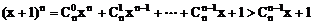
即(x+1)n>nx+1,原不等式成立。
评注:由于(a+b)n的展开式共有n+1项,故可通过对某些项的取舍来达到近似计算或证明不等式的目的。
例8、盒中有6只灯泡,其中2只次品,4只正品,有放回地从中任取两次,每次取一只,试求下列事件的概率:
(1)取到的2只都是次品;
(2)取到的2只中正品、次品各一只;
(3)取到的2只中至少有一只正品。
解:从6只灯泡中有放回地任取两只,共有62=36种不同取法
(1)取到的2只都是次品情况为22=4种,因而所求概率为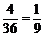
(2)由于取到的2只中正品、次品各一只有两种可能:第一次取到正品,第二次取到次品;及第一次取到次品,第二次取到正品。因而所求概率为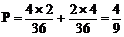
(3)由于“取到的两只中至少有一只正品”是事件“取到的两只都是次品”的对立事件,因而所求概率为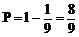
例9、甲、乙两人独立地破译1个密码,他们能译出的密码的概率分别为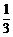 和
和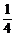 ,求:
,求:
(1)恰有1人译出的密码的概率;
(2)至多1人译出的密码的概率;
(3)若达到译出的密码的概率为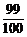 ,至少需要多少个乙这样的人。
,至少需要多少个乙这样的人。
解:记“甲译出密码”为事件A,“甲译不出密码”这事件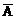 ;记“乙译出密码”为事件B,“乙译不出密码”为事件
;记“乙译出密码”为事件B,“乙译不出密码”为事件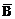 ;“两人都译出密码”为事件C,“两人都译不出密码”为事件D;“恰有1人译出密码”为事件E;“至多1人译出密码”为事件F。
;“两人都译出密码”为事件C,“两人都译不出密码”为事件D;“恰有1人译出密码”为事件E;“至多1人译出密码”为事件F。
(1)“恰有1人译出密码”是包括2种情况:一种是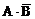 ,另一种是
,另一种是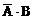 。这两种情况不能同时发生,是互斥的。
。这两种情况不能同时发生,是互斥的。
∴ 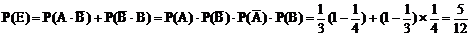
(2)“至多1人译出密码”包括两种情况:“2人都译不出密码”或“恰有1人译出密码”,即事件D+E,且事件D、E是互斥的
∴ 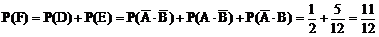
(3)n个乙这样的人都译不出密码的概率为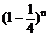 ,根据题意得:
,根据题意得: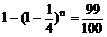
解得:n=16
例10、某数学家有两盒火柴,每盒都有n根火柴,每次用火柴时他在两盒中任取一盒并从中抽出一根,求他发现用完一盒时另一盒还有r根(1≤r≤n)的概率。
解析:由题意知:数学家共用了2n-r根火柴,其中n根取自一盒火柴,n-r根取自另一盒火柴。
由于数学家取火柴时,每次他在两盒中任取一盒并从中抽取一根,故他用完的那一盒取出火柴的概率是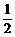 ,他不从此盒中取出一根火柴的概率也是
,他不从此盒中取出一根火柴的概率也是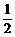 。
。
由于所取的2n-r根火柴,有n根取自用完的那一盒的概率为:
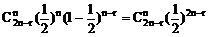
(一) 选择题
1、某一排共12个座位,现甲、乙、丙三人按如下要求入座,每人左右两旁都有空座位,且三人的顺序是甲必须在另两人之间,则不同的座法共有
A、60种 B、112种 C、242种 D、672种
2、某同学从6门课中选学2门,其中有2门课上课时间有冲突,另有2门不允许同时选学,则该同学可选学的方法总数有
A、8种 B、13种 C、12种 D、9种
3、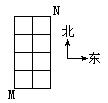 如图,在某城市中,M、N两地间有整齐的道路网,若规定只能向东或向北两个方向沿图中的矩形的边前进,则从M到N不同的走法共有
如图,在某城市中,M、N两地间有整齐的道路网,若规定只能向东或向北两个方向沿图中的矩形的边前进,则从M到N不同的走法共有
A、13种 B、15种 C、25种 D、10种
4、将n个不同的小球放入n个不同的盒子里,恰好有一个空盒的放法种数是
A、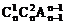 B、
B、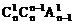 C、
C、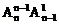 D、
D、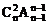
5、若(1-2x)9=a0+a1x+a2x2+…+a8x8+a9x9,则a1+a2+…+a8的值为
A、-1 B、-2 C、-512 D、510
6、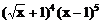 展开式中,x4的系数为
展开式中,x4的系数为
A、-40 B、10 C、40 D、45
7、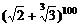 的展开式中无理项的个数是
的展开式中无理项的个数是
A、84 B、85 C、86 D、87
8、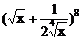 的展开式中系数最大的项是
的展开式中系数最大的项是
A、第3项 B、第4项 C、第2或第3项 D、第3或第4项
9、掷三颗骰子(各面上分别标以数字1到6的均匀正方体玩具),恰有一颗骰子出1点或6点的概率是
A、 B、
B、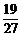 C、
C、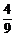 D、
D、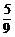
10、一工人看管三台机床,在一小时内甲、乙、丙三台机床需要工人照看的概率分别是0.9,0.8和0.85,那么在一小时中至少有一台机床不需要照看的概率是
A、0.003 B、0.612 C、0.388 D、0.027
11、在4次独立重复试验中,随机事件A恰好发生1次的概率不大于其恰好发生两次的概率,则事件A在一次试验中发生的概率P的取值范围是
A、[0.4,1] B、(0,0.4] C、(0,0.6] D、[0.6,1)
12、一批零件10个,其中有8个合格品,2个次品,每次任取一个零件装配机器,若第一次取得合格品的概率是P1,第二次取得合格品的概率是P2,则
A、P1>P2 B、P1=P2 C、P1<P2 D、P1=2P2
13、一个学生通过某种英语听力测试的概率是1/2,他连续测试n次,要保证他至少有一次通过的概率大于0.9,那么n的最小值为
A、3 B、4 C、5 D、6
14、甲、乙两人投篮命中的概率分别为p、q,他们各投两次,若p=1/2,且甲比乙投中次数多的概率恰好等于7/36,则q的值为
A、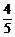 B、
B、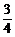 C、
C、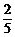 D、
D、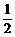
(二) 填空题
15、空间12个点,其中5个点共面,此外无任何4个点共面,这12个点最多可决定_________个不同的平面。
16、(4+2x+x2)(2-x)7展开式中x5的系数为________。
17、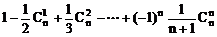 =__________。
=__________。
18、有1个数字难题,在半小时内,甲能解决它的概率是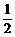 ,乙能解决它的概率是
,乙能解决它的概率是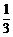 ,两人试图独立地在半小时内解决它,则:两人都未解决的概率为__________;问题得到解决的概率为__________。
,两人试图独立地在半小时内解决它,则:两人都未解决的概率为__________;问题得到解决的概率为__________。
19、一次考试出了10个选择题,每道题有4个可供选择的答案,其中1个是正确的,3个是错误的,某学生只知道5个题的正确答案,对其他5个题全靠猜回答,那么这个学生卷面上正确答案不少于7个题的概率是_________。
(三) 解答题
20、某天的课程表要排入政治、语文、数学、物理、体育、美术共6节课,如果第1节不排体育,最后1节不排数学,那么共有多少种不同的排课表的方法。
21、有甲、乙、丙三位老师,分到6个班上课:
(1)每人上2个班课,有多少种分法?
(2)甲、乙都上1个班课,丙上4个班课,有多少种分法?
(3)2人各上1个班课,1个人上4个班课,有多少种分法?
22、在x(1-x)k+x2(1+2x)8+x3(1+3x)12的展开式中,含x4的系数是144,求k的值并求出含x2项的系数等于多少?
23、某气象站天气预报的准确率为80%,求:
(1)5次预报中恰有4次准确的概率;
(2)5次预报中至少有4次准确的概率(结果保留2位有效数字)。
24、有6个房间安排4个旅游者住,每人可以进住任一房间,且进住房间是等可能的,试求下列事件的概率:
(1)事件A:指定的4个房间各有1人;
(2)事件B:恰有4个房间中各有1人;
(3)事件C:指定的某个房间中有2人;
(4)事件D:第1号房间有1人,第2号房间有3人。
25、有甲、乙两批种子,发芽率分别为0.8,0.7,从两批种子中各取1粒,求:
(1)2粒种子都能发芽的概率;
(2)至少有1粒种子发芽的概率;
(3)恰好有1粒种子发芽的概率。
26、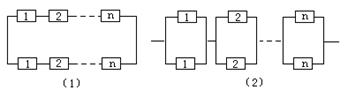 如图构成系统的每个元件的可靠性为r(0<r,r<1),且各个元件能否正常工作是相互独立的,试求图中两种系统的可靠性。
如图构成系统的每个元件的可靠性为r(0<r,r<1),且各个元件能否正常工作是相互独立的,试求图中两种系统的可靠性。
第十讲 复习排列、组合、二项式定理和概率参考答案
参考答案
(一) 选择题
1、B 2、B 3、B 4、A 5、D 6、D 7、A 8、C 9、C 10、C
11、A 12、B 13、B 14、C
(二) 填空题
15、211 16、-336
17、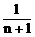 18、(1)1/3 (2)2/3 19、0.3671875
18、(1)1/3 (2)2/3 19、0.3671875
(三) 解答题
20、504 21、(1)90 (2)30 (3)90 22、4,-3
23、(1)0.41 (2)0.74
24、(1)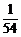 (2)
(2)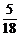 (3)
(3)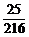 (4)
(4)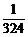
25、(1)0.56 (2)0.94 (3)0.38
26、(1)rn(2-rn) (2)rn(2-r)n (2)比(1)可靠