
极限与导数复习
本章主要内容是极限和导数的概念与运算法则,以及导数在几何、函数等方面的应用。
(1)极限是本章也是整个微积分的基础概念,它包括数列极限和函数极限,它们都是是在无限变化过程中(n→∞,x→∞或x→x0)的变化趋势,这一共同点决定了两类极限有类似的运算性质;如果两个数列(或函数)有极限,那么它们的和、差、积、商的极限分别等于这两个数列(或函数)的极限的和、差、积、商(作为除数的数列或函数的极限不能为0)。其原因在于无穷数列{an}是定义域为N+的特殊函数an=f(n),数列的极限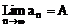 是函数极限
是函数极限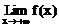 =A的特例。
=A的特例。
极限概念及运算性质决定了确定极限的两种方法:一是利用数形结合思想,从量变中认识质变的数学思想方法,即极限方法。利用极限的方法求出了变速直线运动的瞬时速度与曲线上某点的切线方程,并从中抽象出函数的导数概念。导数是一种特殊的函数极限,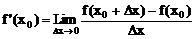 ,x0变化时,f’(x0)就是导函数,二是利用极限的运算法则,可推导出最常用的导数公式与运算法则:c’=0(c为常数),(xn)’=nxn-1(n∈N+),[f(x)±g(x)]’=f’(x)±g’(x),[cf(x)]’=cf’(x),进一步可以求出所有多项式函数的导数。
,x0变化时,f’(x0)就是导函数,二是利用极限的运算法则,可推导出最常用的导数公式与运算法则:c’=0(c为常数),(xn)’=nxn-1(n∈N+),[f(x)±g(x)]’=f’(x)±g’(x),[cf(x)]’=cf’(x),进一步可以求出所有多项式函数的导数。
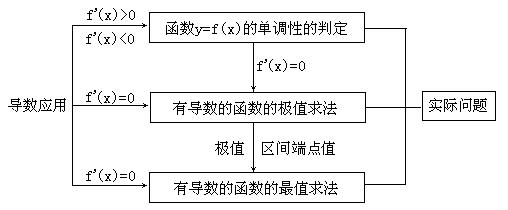 (2)导数f’(x)是函数平均变化率
(2)导数f’(x)是函数平均变化率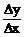 的极限
的极限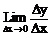 ,瞬时速度、切线斜率、经济学中的边际成本都与平均变化率有关,因而导数有广泛的作用。
,瞬时速度、切线斜率、经济学中的边际成本都与平均变化率有关,因而导数有广泛的作用。
(3)本章思想方法
①极限思想:在变化中求不变,在运动中求静止的思想;
②数形结合思想,如用导数的几何意义及用导数求单调性、极值等。
例1、 求下列极限
(1)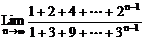 (2)
(2)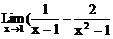 )
)
解题思路分析:
(1)因分子及分母的次数随n增大而增加,故不能利用运算性质。先求和化简。
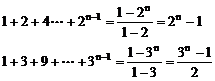
∴ 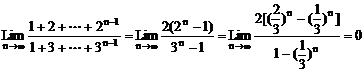
(2)当x→1时,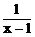 及
及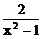 均无意义,应约去因式x-1
均无意义,应约去因式x-1
∵ 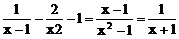
∴ 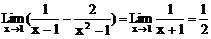
说明:函数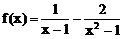 在x=1 无定义,但与
在x=1 无定义,但与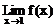 存在无关。一般地有下列结论:如果f(x)=x0处无定义,g(x)在x=x0处有定义并存在极限,且当x≠x0时,f(x)=g(x),则
存在无关。一般地有下列结论:如果f(x)=x0处无定义,g(x)在x=x0处有定义并存在极限,且当x≠x0时,f(x)=g(x),则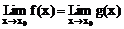 。
。
例2、设函数y=ax3+bx2+cx+d的图象与y轴交点为P,且曲线在P点处的切线方程为12x-y-4=0,若函数在x=2处取得极值0,试确定函数的解析式。
解题思路分析:
P(0,d)
∵ 曲线在点P处切线为12x-y-4=0
∴ x=0时,y=d
∴ d=-4
∵ y’=3ax2+2bx+c
∴ y’|x=0=c
又切线斜率k=12
∴ c=12
又函数在x=2处取得极值0
∴ 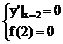
∴ 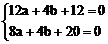
∴ 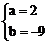
∴ 函数解析式y=2x3-9x2+12x-4
例3、偶函数f(x)=ax4+bx3+cx2+dx+e的图象过点P(0,1),且在x=1处的切线方程为y=x-2
(1)求y=f(x)的解析式;
(2)求y=f(x)的极大(小)值。
解题思路分析:
∵ f(x)是偶函数
∴ b=d=0
又图象过P(0,1)
∴ e=1
此时f(x)=ax4+cx2+1
∵ y’=4ax3+2cx
∴ y’|x=1=4a+2c=1 ①
又切点(1,-1)在曲线上
∴ a+c+1=-1 ②
由①②得: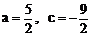
∴ f(x)=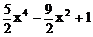
(2)f’(x)=10x3-9x=0
∴ x=0,x=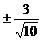
列表可得: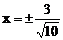 时,f(x)极小=
时,f(x)极小=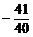
x=0时,f(x)极大=1
例4、曲线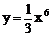 上哪一点的法线在y轴上截距最小?(法线是指过曲线上一点与以此点为切点的切线垂直的直线)
上哪一点的法线在y轴上截距最小?(法线是指过曲线上一点与以此点为切点的切线垂直的直线)
解题思路分析:
在曲线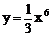 上任取一点(x0,y0),则过该点切线的斜率为k=2x05
上任取一点(x0,y0),则过该点切线的斜率为k=2x05
∴ 法线的斜率为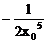
∴ 法线方程y-y0=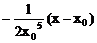
令x=0,使法线在y轴上的截距
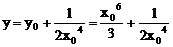
∴ 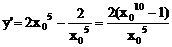
令y’=0,得x0=±1
当x0<-1时,y’<0,∴y单调递减
当-1<x0<0时,y’>0,∴y单调递增
当0<x0<1时,y’<0,∴y单调减小
当x0>1时,y’>0,则y单递增
∴ 当x0=±1时,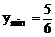 ,此时点(±1,
,此时点(±1,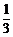 )
)
例5、研究函数f(x)=ax3+bx2-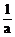 x+1的单调性(a≠0)
x+1的单调性(a≠0)
解题思路分析:
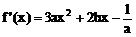
1、a>0时,由f’(x)>0得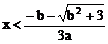 或
或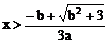
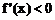 得
得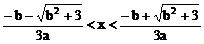
∴ f(x)在(-∞,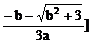 ,
,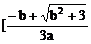 ,+∞)上单调递增;在
,+∞)上单调递增;在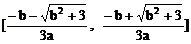 上单调递减。
上单调递减。
2、当a<0时,f(x)在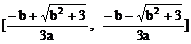 上单调递增;在(-∞,
上单调递增;在(-∞,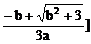 ,
,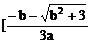 ,+∞)上单调递减。
,+∞)上单调递减。
例6、用总长为14.8m的钢条制作一个长方体容器的框架,如果所制容器的底面的一边比另一边长0.5m,那么为多少时容器的容积最大?并求出它的最大容积?
解题思路分析:
设容器底面短边长为xm,另一边长为(x+0.5)m,高为(3.2-2x)m
∵ 3.2-2x>0,x>0
∴ 0<x<1.6
设容器的容积为ym3
y=x(x+0.5)(3.2-2x)
∴ y=-2x3+2.2x2+1.6x
∴ y’=-6x2+4.4x+1.6
令y’=0得x=1,x=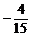 (舍)
(舍)
∵ y在(0,1.6)内只有一个驻点x=1,而x过小或过大时,y值很小
∴ 当x=1时,ymax=1.8,此时高为1.2
(一) 选择题(每小题5分,共60分)
1、 等差数列中,若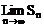 存在,则这样的数列
存在,则这样的数列
A、 有且仅有一个 B、有无数多个 C、有一个或无穷多个 D、不存在
2、 已知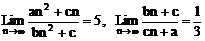 ,如果bc≠0,那么
,如果bc≠0,那么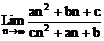 =
=
A、 15
B、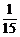 C、
C、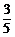 D、
D、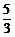
3、 若r为实常数,则集合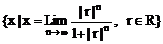
A、恰有一个元素 B、恰有两个元素 C、恰有三个元素 D、无数多个元素
4、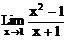 的值
的值
A、2 B、1 C、0 D、不存在
5、函数y=(x2-1)3+1在x=-1处
A、 有极大值 B、无极值 C、有极小值 D、无法确定极值情况
6、 f(x)=ax3+3x2+2,f’(-1)=4,则a=
A、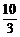 B、
B、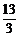 C、
C、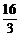 D、
D、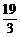
7、过抛物线y=x2上的点M(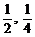 )的切线的倾斜角是
)的切线的倾斜角是
A、300 B、450 C、600 D、900
8、函数f(x)=x3-6bx+3b在(0,1)内有极小值,则实数b的取值范围是
A、 A、(0,1) B、(-∞,1)
C、(0,+∞) D、(0,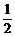 )
)
9、 函数y=x3-3x+3在[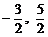 ]上的最小值是
]上的最小值是
A、 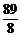 B、1 C、
B、1 C、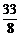 D、5
D、5
10、若f(x)=x3+ax2+bx+c,且f(0)=0为函数的极值,则
A、c≠0 B、当a>0时,f(0)为极大值
C、b=0 D、当a<0时,f(0)为极小值
11、已知函数y=2x3+ax2+36x-24在x=2处有极值,则该函数的一个递增区间是
A、(2,3) B、(3,+∞) C、(2,+∞) D、(-∞,3)
12、方程6x5-15x4+10x3+1=0的实数解的集合中
A、至少有2个元素 B、至少有3个元素 C、至多有1个元素 D、恰好有5个元素
(二) 填空题(每小题4分,共16分)
13、若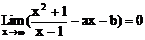 ,则a=______,b=______。
,则a=______,b=______。
14、已知偶函数f(x)在(0,+∞)内满足f’(x)>0,f(0)>0,则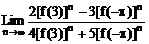 =__________。
=__________。
15、抛物线y=x2上点切线和直线3x-y+1=0的交角为450,则点P坐标为__________。
16、两个和为48的正整数,第一个数的立方与第二个数的平方之和最小,则这两个正整数分别为__________。
(三) 解答题
17、(10分)已知无穷数列{an}存在极限,且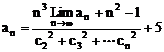 ,求
,求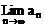 。
。
18、(12分)设函数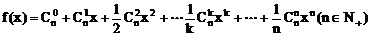 ,求
,求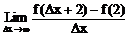 的值。
的值。
19、(12分)已知曲线C1:y=ax2上点P处的切线为1,曲线C2:y=bx3上点A(1,b)处的切线为2,且1⊥2,垂足M(2,2),求a、b的值及点P的坐标。
20、(12分)求函数f(x)=p2x2(1-x)p(p∈N+),在[0,1]内的最大值。
21、(14分)证明双曲线xy=a2上任意一点的切线与两坐标轴组成的三角形面积等于常数。
22、(14分)已知曲线S:y=x3+px2+qx的图象与x轴相切于不同于原点的一点,又函数有极小值-4,求p、q的值。
第十二讲 复习极限与导数参考答案
参考答案
(一)选择题
1、A 2、D 3、C 4、C 5、B 6、A 7、B 8、D 9、B 10、C 11、B 12、C
(二)填空题
13、a=b=1 14、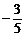 15、(-1,1)或(
15、(-1,1)或(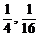 )
16、5与43
)
16、5与43
(三)解答题
17、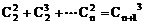 ……3分
……3分
∴ 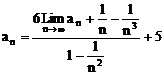 ……6分
……6分
∴ 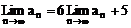 ……9分
……9分
∴ 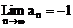 ……10分
……10分
18、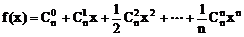
∴ 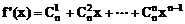 ……4分
……4分
∴ 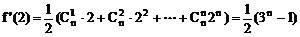 ……8分
……8分
∴  ……12分
……12分
19、设P(t,at2),则1斜率k1=2at
∴ 1:y-at2=2at(x-t) ……2分
2斜率k2=3bx2|x=1=3b
∴ 2:y-b=3b(x-1) ……4分
∵ 1与2于点M(2,2)
∴ 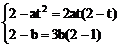
∴ 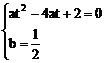 ①
①
又1⊥2
∴ k1k2=0
∴ 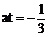 ②
……8分
②
……8分
由①②得t=10,a=-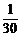
∴ P(10,-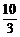 )
……10分
)
……10分
20、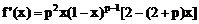 ……4分
……4分
令f’(x)=0得,x=0,x=1,x=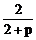 ……6分
……6分
在[0,1]上,f(0)=0,f(1)=0,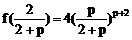 ……10分
……10分
∴ 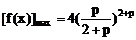 ……12分
……12分
21、设双曲线上任一点P(x0,y0)
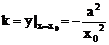 ……4分
……4分
∴ 切线方程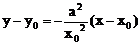 ……6分
……6分
令y=0,则x=2x0 ……8分
令x=0,则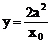 ……10分
……10分
∴ 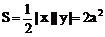 ……12分
……12分
22、y’=3x2+2px+q ……2分
令y’=0,设3x2+2px+q=0两根为x1,x2,x1<x2,列表:
|
x |
(-∞,x1) |
x1 |
(x1,x2) |
x2 |
(x2,+∞) |
|
y’ |
+ |
0 |
- |
0 |
+ |
   y y |
|
极大值 |
|
极小值 |
|
∴ S与x轴相切于点(x1,0),点(x2,-4)在S上 ……6分
 x13+px12+qx1=0
①
x13+px12+qx1=0
①
∴ x23+px22+qx1=-4 ② ……8分
3x12+2px1+q=0 ③
3x22+2px2+q=0 ④
③×x1-①得:x1=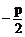
④×x2-②得:2x23+px22=4 ……10分
又x1+x2=-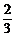 p
p
∴ x2= p,p=6
……12分
p,p=6
……12分
∴ x1=-3,x2=-1
∴ p=6,q=9 ……14分