
1.(全国卷Ⅰ)设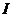 为全集,
为全集,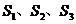 是
是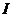 的三个非空子集,且
的三个非空子集,且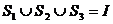 ,则下面论断正确的是(C)
,则下面论断正确的是(C)
(A)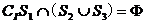 (B)
(B)
(C)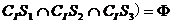 (D)
(D)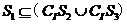
2.(北京卷)设全集U=R,集合M={x| x>1,P={x| x2>1},则下列关系中正确的是(C)
(A)M=P (B)P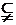 M
(C)M
M
(C)M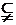 P ( D)
P ( D)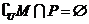
3.(北京卷)“m=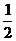 ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的
(B)
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的
(B)
(A)充分必要条件 (B)充分而不必要条件
(C)必要而不充分条件 (D)既不充分也不必要条件
4、(上海卷)已知集合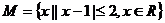 ,
,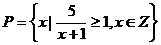 ,则
,则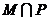 等于
(B)
等于
(B)
A.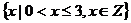 B.
B.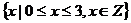
C.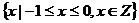 D.
D.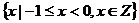
5.(天津卷)设集合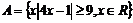 ,
, 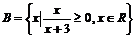 ,
则A∩B= (D)
,
则A∩B= (D)
A.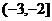 B.
B.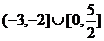 C.
C.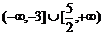 D.
D.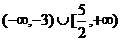
6.(天津卷)给出下列三个命题
①若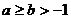 ,则
,则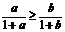
②若正整数m和n满足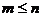 ,则
,则
③设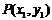 为圆
为圆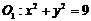 上任一点,圆O2以
上任一点,圆O2以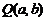 为圆心且半径为1.当
为圆心且半径为1.当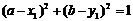 时,圆O1与圆O2相切
时,圆O1与圆O2相切
其中假命题的个数为 ( B )
A.0 B.1 C.2 D.3
7.(天津卷)设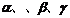 为平面,
为平面,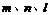 为直线,则
为直线,则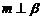 的一个充分条件是 (D
)
的一个充分条件是 (D
)
A. 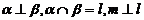 B.
B. 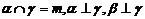
C. 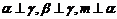 D.
D. 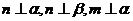
(D)
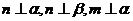
8. (福建卷)已知集合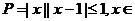 R|,
R|, 等于(D)
等于(D)
A.P B.Q C.{1,2} D.{0,1,2}
9.(福建卷)已知直线m、n与平面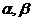 ,给出下列三个命题:
,给出下列三个命题:
①若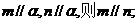
②若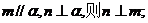
③若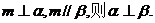
其中真命题的个数是 ( C )
A.0 B.1 C.2 D.3
10.(福建卷)已知p: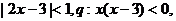 则p是q的(
A )
则p是q的(
A )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
11.(广东卷)若集合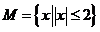 ,
,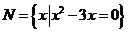 ,则
,则 (B)
(B)
(A)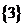 (B)
(B) (C)
(C)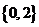 (D)
(D)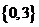
12.(广东卷)给出下列关于互不相同的直线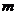 、
、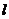 、
、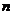 和平面
和平面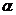 、
、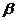 的四个命题:
的四个命题:
①若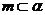 ,
,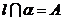 ,点
,点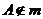 ,则
,则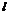 与
与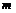 不共面;
不共面;
②若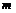 、
、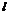 是异面直线,
是异面直线,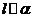 ,
,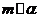 ,且
,且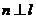 ,
,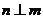 ,则
,则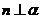 ;
;
③若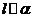 ,
,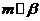 ,
,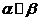 ,则
,则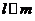 ;
;
④若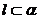 ,
,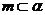 ,
,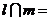 点
点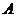 ,
,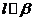 ,
,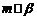 ,则
,则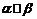 .
.
其中为假命题的是(C)
(A)①(B)②(C)③(D)④
13.(湖北卷)设P、Q为两个非空实数集合,定义集合
P+Q=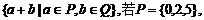
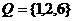 ,则P+Q中元素的个数是 ( B )
,则P+Q中元素的个数是 ( B )
A.9 B.8 C.7 D.6
14.(湖北卷)对任意实数a,b,c,给出下列命题:
①“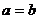 ”是“
”是“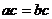 ”充要条件; ②“
”充要条件; ②“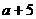 是无理数”是“a是无理数”的充要条件③“a>b”是“a2>b2”的充分条件;④“a<5”是“a<3”的必要条件.
是无理数”是“a是无理数”的充要条件③“a>b”是“a2>b2”的充分条件;④“a<5”是“a<3”的必要条件.
其中真命题的个数是 ( B )
A.1 B.2 C.3 D.4
15.(江苏卷)设集合A={1,2},B={1,2,3},C={2,3,4}则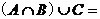 (D
)
(D
)
( A ) {1,2,3} ( B ) {1,2,4} ( C ) {2,3,4} ( D ) {1,2,3,4}
16(江苏卷)设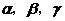 为两两不重合的平面,l,m,n为两两不重合的直线,给出下列四个命题:
为两两不重合的平面,l,m,n为两两不重合的直线,给出下列四个命题:
① 若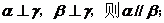 ②若
②若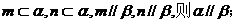 ③
③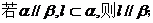 ④
④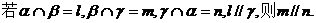
其中真命题的个数是(B )
( A ) 1 ( B ) 2 ( C ) 3 ( D )4
17.(江西卷)设集合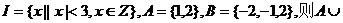 (
(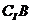 )=(D)
)=(D)
A.{1} B.{1,2} C.{2} D.{0,1,2}
18.(江西卷) “a=b”是“直线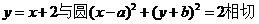 ”的 (A )
”的 (A )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分又不必要条件
19(辽宁卷)极限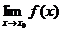 存在是函数
存在是函数 在点
在点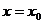 处连续的 (B)
处连续的 (B)
A.充分而不必要的条件 B.必要而不充分的条件
C.充要条件 D.既不充分也不必要的条件
20.(辽宁卷)已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列四个命题:①若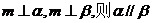 ;
②若
;
②若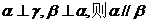 ;
;
③若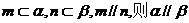 ;
;
④若m、n是异面直线,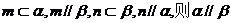
其中真命题是 (D )
A.①和② B.①和③ C.③和④ D.①和④
21.(浙江卷)设全集U={1,2,3,4,5,6,7},P={1,2,3,4,5},Q={3,4,5,6,7},则P∩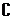 Uq=( A )
Uq=( A )
(A) {1,2} (B) (3,4,5) (C) {1,2,6,7} (D) {1,2,3,4,5}
22.(浙江卷)设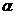 、
、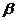 为两个不同的平面,l、m为两条不同的直线,且l
为两个不同的平面,l、m为两条不同的直线,且l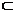
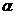 ,m
,m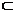
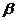 ,有如下的两个命题:①若
,有如下的两个命题:①若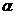 ∥
∥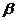 ,则l∥m;②若l⊥m,则
,则l∥m;②若l⊥m,则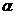 ⊥
⊥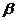 .
.
那么 ( D )
(A) ①是真命题,②是假命题 (B) ①是假命题,②是真命题
(C) ①②都是真命题 (D) ①②都是假命题
23.(浙江卷)设f(n)=2n+1(n∈N),P={1,2,3,4,5},Q={3,4,5,6,7},记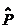 ={n∈N|f(n)∈P},
={n∈N|f(n)∈P}, ={n∈N|f(n)∈Q},则(
={n∈N|f(n)∈Q},则(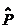 ∩
∩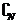
 )∪(
)∪( ∩
∩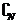
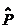 )=( A )
)=( A )
(A) {0,3} (B){1,2} (C) (3,4,5) (D){1,2,6,7}
24.(湖南卷)设全集U={-2,-1,0,1,2},A={-2,-1,0},B={0,1,2},则( UA)∩B=
(C)
A.{0} B.{-2,-1} C.{1,2} D.{0,1,2}
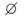 25.(湖南卷)设集合A={x|
25.(湖南卷)设集合A={x|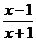 <0
<0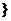 ,B={x || x -1|<a
,B={x || x -1|<a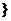 ,若“a=1”是“A∩B≠ ”的( A )
,若“a=1”是“A∩B≠ ”的( A )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
26.(湖南卷)集合A={x|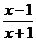 <0=,B={x || x -b|<a
<0=,B={x || x -b|<a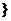 ,若“a=1”是“A∩B≠
,若“a=1”是“A∩B≠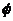 ”的充分条件,
则b的取值范围是 (D)
”的充分条件,
则b的取值范围是 (D)
A.-2≤b<0 B.0<b≤2 C.-3<b<-1 D.-1≤b<2
填空题:
1.(福建卷)把下面不完整的命题补充完整,并使之成为真命题:
若函数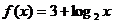 的图象与
的图象与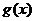 的图象关于
对称,则函数
的图象关于
对称,则函数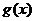 =
=
。
(注:填上你认为可以成为真命题的一件情形即可,不必考虑所有可能的情形).
.如 ①x轴,-3-log2x ②y轴,3+log2(-x)
③原点,-3-log2(x) ④直线y=x, 2x-3
2.(江西卷)以下同个关于圆锥曲线的命题中:①设A、B为两个定点,k为非零常数,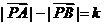 ,则动点P的轨迹为双曲线;②设定圆C上一定点A作圆的动点弦AB,O为坐标原点,若
,则动点P的轨迹为双曲线;②设定圆C上一定点A作圆的动点弦AB,O为坐标原点,若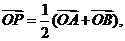 则动点P的轨迹为椭圆;③方程
则动点P的轨迹为椭圆;③方程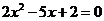 的两根可分别作为椭圆和双曲线的离心率;④双曲线
的两根可分别作为椭圆和双曲线的离心率;④双曲线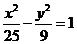 与椭圆
与椭圆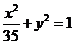 有相同的焦点.
有相同的焦点.
其中真命题的序号为 ③④ (写出所有真命题的序号)