
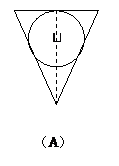
1.在一个倒置的正三棱锥容器内,放入一个钢球,钢球恰好与棱锥的四个面都接触,经过棱锥的一条侧棱和高作截面,正确的截面图形是( )



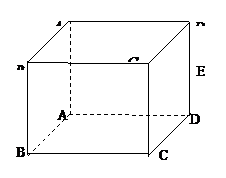
2.如右图,点E是正方体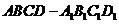
的棱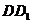 的中点,则过点E与直线
的中点,则过点E与直线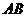 和
和
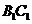 都相交的直线的条数是( )
都相交的直线的条数是( )
(A)0条 (B)1条 (C)2条 (D)无数
3.在正方体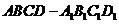 中,写出过顶
中,写出过顶
点A的一个平面______________,使该平面与正方体的12条棱所在的直线所成的角均相等(注:填上你认为正确的一个平面即可,不必考虑所有可能的情况)。
热点之二:空间角与距离问题
三个角:包括两条直线所成的角、直线与平面所成的角、二面角;
八个距离:包括点到直线的距离、点到面的距离、两条平行直线的距离、异面直线
的距离、直线与平行平面的距离、两个平行平面之间的距离、球面上两点的距离。
在求角或距离时,一定要“先找后解”。
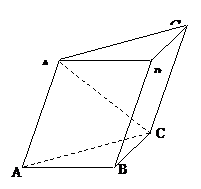 [例3](1998年全国高考题)已知斜三棱柱
[例3](1998年全国高考题)已知斜三棱柱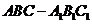 的侧面
的侧面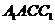 与底面
与底面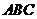 垂直,
垂直,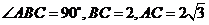 ,
,
且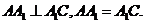
(Ⅰ)求侧棱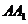 与底面
与底面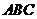 所成角的大小;
所成角的大小;
(Ⅱ)求侧面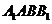 与底面
与底面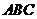 所成二面角的大小;
所成二面角的大小;
(Ⅲ)(理)求顶点C到侧面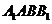 的距离;
的距离;
(Ⅲ)(文)求侧棱 和侧面
和侧面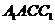 的距离。
的距离。
(练习)
4.如图,在正方体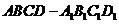 中,E、F分别为
中,E、F分别为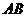 、
、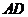 的中点,
的中点,
 (1)
(1)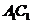 与
与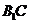 所成角的大小是_____________;
所成角的大小是_____________;
(2) 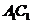 与
与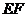 所成角的大小是_____________;
所成角的大小是_____________;
(3) 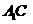 与
与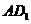 所成角的大小是_____________;
所成角的大小是_____________;
(4)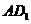 与
与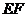 所成角的大小是_____________;
所成角的大小是_____________;
(5)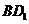 与
与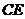 所成角大小是_____________;
所成角大小是_____________;
(6)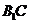 与平面
与平面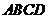 所成角的大小是_________;
所成角的大小是_________;
(7)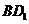 与平面
与平面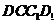 所成角的大小是_____________;
所成角的大小是_____________;
(8)二面角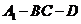 的大小是_________;
的大小是_________;
(9)二面角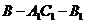 的大小是_____________;
的大小是_____________;
(10)二面角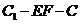 的大小是_____________;
的大小是_____________;
5.将锐角为60°,边长为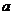 的菱形
的菱形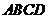 沿较短的对角线BD折成60°的二面角后,
沿较短的对角线BD折成60°的二面角后,
 (1)求异面直线
(1)求异面直线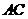 与
与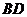 的距离;
的距离;
(2)求三棱锥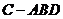 的体积;
的体积;
(3)求D到面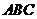 的距离。
的距离。
热点之三:表面积与体积问题
[例4]棱锥被平行于底面的平面所截,当截面分别平分侧棱、侧面积、体积时,相应截面面积记作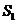 、
、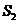 、
、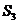 ,则(
)
,则(
)
(A)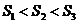 (B)
(B)
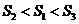
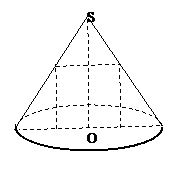 (C)
(C)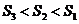 (D)
(D)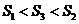
[例5]如右图,在母线长为2的等边圆锥内作一个内接圆柱,
当这个圆柱体积最大时,它的高是( )
(A)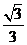 (B)
(B)
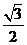 (C)
(C)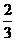 (D)
(D)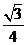

(练习)
6.如图,三棱台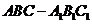 的上底
的上底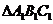 面积
面积
为4,下底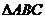 面积为9,且三棱锥
面积为9,且三棱锥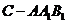 的体
的体
积为9,则三棱台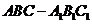 的体积为(
)
的体积为(
)
(A)19
(B)18 (C)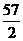 (D)
(D)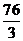
7.已知圆台上、下底面半径分别为1cm和4cm,圆台的侧面展开图扇环所对的圆心角为216°,则该圆台的体积为_________________________。
8.直四棱柱 的体积等于1,底面
的体积等于1,底面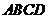 为平行四边形,则四面体
为平行四边形,则四面体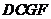 体积为
体积为
____________。
热点之四:立几综合题
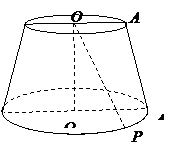 [例6]如图,圆台
[例6]如图,圆台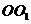 的高等于下底面圆的半径,母线
的高等于下底面圆的半径,母线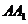 与下底面成
与下底面成 的角,P为下底面圆周上的一点,
的角,P为下底面圆周上的一点,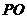 与
与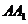 成
成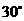 的角。
的角。
(Ⅰ)求二面角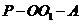 的余弦值;
的余弦值;
(Ⅱ)若下底面圆的半径为1,求圆台的侧面积。
 [例7]如图,直四棱柱
[例7]如图,直四棱柱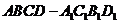 的侧棱
的侧棱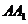 的长是a,底面ABCD是边长AB=2a,BC=a的矩形,E为
的长是a,底面ABCD是边长AB=2a,BC=a的矩形,E为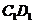 的中点。
的中点。
(Ⅰ)求证:平面BCE⊥平面BDE;
(Ⅱ)求二面角E-BD-C的大小;
(Ⅲ)求三棱锥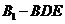 的体积.
的体积.
(练习答案)
1、B 2、B
3、面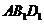 4、(1)
4、(1) (2)
(2)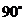 (3)
(3)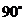 (4)
(4) (5)
(5)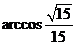 (6)
(6)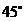 (7)
(7)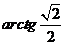 (8)
(8)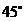 (9)
(9)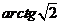 (10)
(10)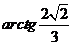
5、(1)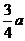 (2)
(2)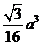 (3)
(3)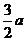 6、C 7、
6、C 7、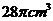 8、
8、