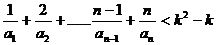1. 了解导数概念的某些实际背景(如瞬时速度、加速度、光滑曲线切线的斜率等).
2. 掌握函数的导数公式,会求多项式函数的导数.
[解题目标]
1. 会用导数求多项式函数的单调区间.
2. 可导函数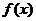 在(
在(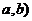 单调递增的充要条件是
单调递增的充要条件是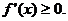
[例题讲解]
例题1(1)已知函数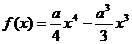 在(
在(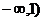 内是增函数,在(
内是增函数,在(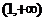 内是减函数,则( )
内是减函数,则( )
A 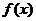 的极大值是
的极大值是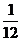 B
B
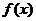 的极小值是-
的极小值是-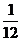
C 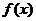 的极大值是0 D
的极大值是0 D
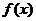 的极小值是
的极小值是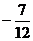
(2)函数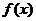
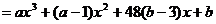 的图象关于原点成中心对称,则
的图象关于原点成中心对称,则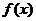 ( )
( )
A 在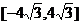 上为增函数 B
在
上为增函数 B
在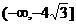 上为减函数
上为减函数
C 在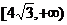 上为增函数,在
上为增函数,在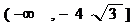 上为减函数
上为减函数
D 在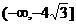 上为增函数,在
上为增函数,在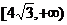 上为增函数
上为增函数
(3)路灯距地平面为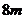 ,一个身高
,一个身高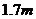 的人以
的人以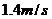 的速度匀速地从路灯的正底下,沿某直线离开路灯,那么人影长度的变化速率
的速度匀速地从路灯的正底下,沿某直线离开路灯,那么人影长度的变化速率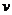 为( )
为( )
A 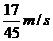 B
B
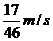 C
C
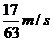 D
D 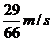
(4)若函数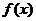
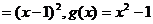 ,则
,则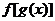 的单调递减区间为_______,单调递增区间为________.
的单调递减区间为_______,单调递增区间为________.
(5)已知函数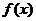
 ,若
,若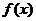 的单调减区间为
的单调减区间为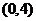 ,则
,则
(6)设函数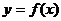 在定义域内可导,导函数
在定义域内可导,导函数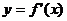 的图象如图,则函数
的图象如图,则函数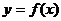 的图象可能为( )
的图象可能为( )
例2 设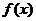 =
=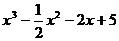
(1)求函数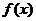 的单调区间.
的单调区间.
(2)当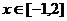 时,
时,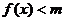 恒成立,求实数
恒成立,求实数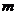 的取值范围.
的取值范围.
例3 若函数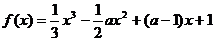 在区间(1,4)内为减函数,在区间(
在区间(1,4)内为减函数,在区间(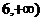 上为增函数,试求实数
上为增函数,试求实数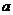 的范围.
的范围.
例4 已知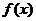
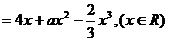 在区间[-1,1] 上是增函数
在区间[-1,1] 上是增函数
(1)求实数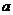 的值组成的集合A
的值组成的集合A
(2)设关于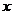 的方程
的方程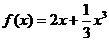 的两个非零实根为
的两个非零实根为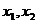 ,试问:是否存在实数
,试问:是否存在实数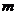 ,使得不等式
,使得不等式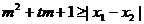 对任意
对任意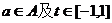 恒成立?若存在,求出
恒成立?若存在,求出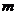 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
高三数学第二轮复习教学案
第二十二课时 导数与函数的最值
班级 学号 姓名
[考纲解读]
理解极大值、极小值、最大值、最小值的概念,并会求用导数求多项式函数的单调区间、极大值、极小值及闭区间上的最值.
[解题目标]
1.能利用导数求函数的最大值、最小值.
2.会求某些简单实际问题的最大值和最小值.
[例题讲解]
例题1(1)设函数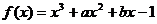 ,若当
,若当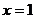 时,有极值1,则
时,有极值1,则 ( )
( )
A -1 B
0 C 1 D
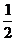
(2)若函数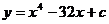 有最小值
有最小值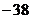 ,则c=_________.
,则c=_________.
A 4 B 5 C 8 D 10
(3)已知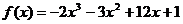 在区间[
在区间[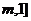 上的最小值为
上的最小值为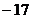 ,则
,则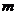 的值为________.
的值为________.
(4)已知函数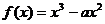 ,若
,若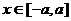 ,则
,则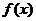 的最大值为_________.
的最大值为_________.
(5)若函数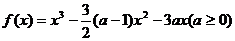 ,且在区间[-1,2]上的最小值为0,则
,且在区间[-1,2]上的最小值为0,则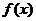 的最大值为________.
的最大值为________.
(6)当半径为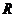 的球的内接圆锥的体积最大时,高为________.
的球的内接圆锥的体积最大时,高为________.
例2 函数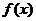 是定义在[-1,0)
是定义在[-1,0)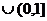 上的偶函数,当
上的偶函数,当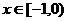 时,
时,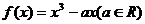
(1)当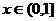 时,求
时,求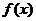 的解析式.
的解析式.
(2)若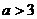 ,试判断
,试判断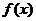 在
在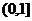 的单调性,并证明你的结论.
的单调性,并证明你的结论.
(3)是否存在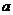 ,使得当
,使得当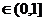 时,
时,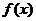 有最大值-1.
有最大值-1.
例3 某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规化建成一个矩形的高科技工业园区,已知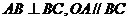 ,且
,且 ,曲线段
,曲线段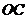 是以点
是以点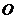 为顶点且开口向上的抛物线的一段,如果要使矩形的相邻两边分别落在
为顶点且开口向上的抛物线的一段,如果要使矩形的相邻两边分别落在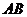 、
、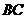 上,且一个顶点落在曲线段
上,且一个顶点落在曲线段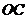 上,问应如何规划,才能使矩形工业园区的用地面积最大?并求出最大的用地面积.(精确到0.1km2)
上,问应如何规划,才能使矩形工业园区的用地面积最大?并求出最大的用地面积.(精确到0.1km2)
例4 设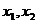 是函数
是函数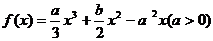 的两个极值点,且
的两个极值点,且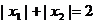 .
.
(1)证明: .
.
(2)若函数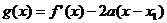 ,证明:当
,证明:当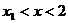 且
且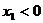 时,
时,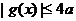
高三数学第二轮复习教学案
第二十三课时 导数与函数的切线
班级 学号 姓名
[考纲解读]
1.了解导数概念的某些实际背景,如光滑曲线切线的斜线等.
2.掌握函数在一点处的导数的定义和导数的几何意义.
[教学目标]
1.会求过一点的曲线的切线方程.
2.会求一些与函数图象的切线相关的问题.
[例题讲解]
例题1(1)若直线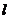 过点
过点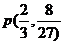 ,且与曲线
,且与曲线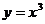 相切于点
相切于点 ,则
,则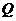 点坐标为________.
点坐标为________.
(2)若过抛物线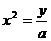 焦点的直线与抛物线交于
焦点的直线与抛物线交于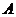 、
、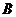 两点,则过点
两点,则过点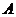 、
、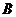 的两条切线的夹角( )
的两条切线的夹角( )
A 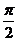 B
B
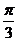 C
C
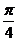 D
D
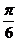
(3)函数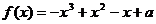 与直线
与直线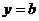 ( )
( )
A 有三个交点 B 有两个交点 C 有且只有一个交点 D 相切
(4)已知抛物线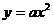 在点
在点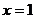 处的切线与圆
处的切线与圆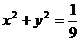 相切,则
相切,则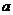 的值为( )
的值为( )
A 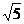 B
B
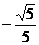 C
C
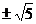 D
D
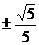
(5)曲线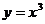 在点(
在点(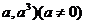 处的切线与
处的切线与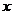 轴,直线
轴,直线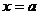 所围成的三角形的面积为
所围成的三角形的面积为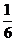 ,则
,则
(6)已知曲线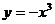 在点
在点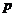 处的切线
处的切线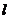 在
在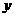 轴上的截距为2,则
轴上的截距为2,则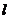 的方程为___________,过
的方程为___________,过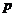 点的曲线
点的曲线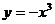 的切线方程为_______.
的切线方程为_______.
例2 已知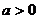 ,函数
,函数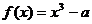 ,
,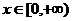 ,设
,设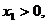 记曲线
记曲线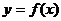 在点
在点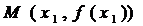 处的切线为
处的切线为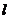 .
.
(1) 求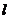 的方程
的方程
(2) 设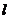 与
与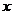 轴交于点
轴交于点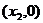
证明:①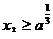 ②若
②若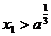 ,则
,则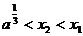
例3 函数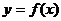 在区间
在区间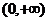 内可导,导函数
内可导,导函数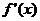 是减函数,且
是减函数,且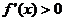 ,设
,设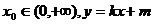 是曲线
是曲线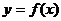 在点(
在点(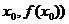 处的切线方程,并设函数
处的切线方程,并设函数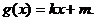
(1)
用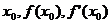 表示
表示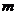
(2)
证明:当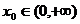 时,
时,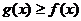
例4 过点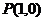 作曲线
作曲线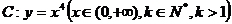 的切线切点为
的切线切点为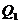 ,设
,设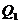 点在
点在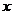 轴上的投影是点
轴上的投影是点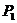 ,又过点
,又过点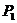 作曲线C的切线切点为
作曲线C的切线切点为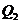 ,设
,设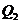 在
在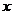 轴上的投影是
轴上的投影是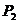 ,……,依此下去,得到一系列点
,……,依此下去,得到一系列点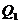 、
、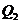 …、
…、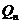 、…,设点
、…,设点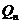 的横坐标为
的横坐标为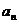 .
.
(1)求证: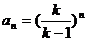
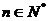
(2)求证: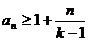
(3)求证: