
1、会用导数的定义求简单函数的导数。
2、正确运用导数的运算法则求多项式函数的导数。
3、会求出曲线上一点或曲线外一点的切线方程。
知识概要
1、导数的概念及运算法则。
2、导数的几何意义。
重点、难点
1、根据函数式的特征,灵活运用相关公式对原函数式变形,求出导数或导函数。
2、如何求曲线上一点或曲线外一点的切线方程。
基础练习
1、(1)若函数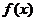 =
=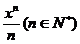 ,则
,则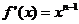 ;
;
(2)若常数函数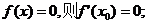
(3)若函数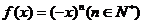 ,则
,则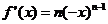 ;
;
(4)若函数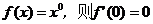 。
。
以上命题正确的是__________________
2、(1)函数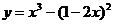 的导函数为_______________;
的导函数为_______________;
(2)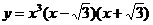 的导函数为_____________;
的导函数为_____________;
3、若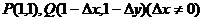 是曲线y=x2的两点,则割线PQ的斜率为_____。
是曲线y=x2的两点,则割线PQ的斜率为_____。
4、设曲线y=x3-3x在点P处的切线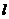 过点(0,16),则
过点(0,16),则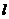 的方程________。
的方程________。
例题讲解
例1 :已知函数f(x)=x5-5ax2+5x+a且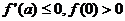 ,求f(x)的解析式。
,求f(x)的解析式。
例2:已知曲线C:y=ax4+bx3+cx2+dx+e过点A(0,-1)且关于y轴对称,若C在x=1处的切线方程2x+y-2=0,求曲线C的方程。
例3:O是原点,直线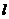 过抛物线C:y=x2上一点P,直线
过抛物线C:y=x2上一点P,直线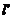 与C相切于点P,
与C相切于点P,
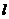 、
、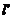 分别与y轴、C的准线相交于点Q、R,且
分别与y轴、C的准线相交于点Q、R,且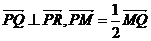
(1)求点M的轨迹方程;
(2)设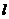 的方向向量为
的方向向量为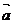 ,试说明使得
,试说明使得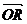 ∥
∥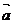 点P是否存在。
点P是否存在。
课后作业
班级_______学号__________姓名_________
1、
求导f(x)=(x-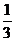 )2(x2+
)2(x2+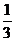 x+
x+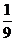 )2:____________
)2:____________
2、
若函数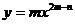 的导数为
的导数为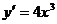 ,则m=__________,n=__________
,则m=__________,n=__________
3、
若曲线y=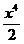 +x过点P的切线垂直于直线y=
+x过点P的切线垂直于直线y=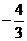 x,则这条切线的方程_______
x,则这条切线的方程_______
4、 设曲线y=-x3+3x2-3x2 -2x+10的切线的倾斜角为α,则α的取值范围_______
5、 已知曲线y=x3-2x2+x在点P1、P2处的切线斜率都为1,则P1P2在x轴的射影长为( )
A 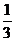 B
B
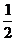 C
C
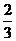 D
D
6、已知使f(x)=x3+ax2-4a的导数为0的x的值也使f(x)的值为0,求a的值。
7、(1)f(x)=2ax3+3bx2+2abx(a>0,b>0)且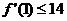 ,求ab=1时,f(x)的解析式。
,求ab=1时,f(x)的解析式。
(2)已知曲线y=ax4+bx3+cx+1关于点(0,1)对称,且在点(1,0)处的切线斜率为1,求a、b、c。
8、已知函数f(x)=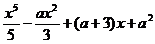 ,且对任意x∈R,
,且对任意x∈R,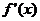 ≥0,求a的范围。
≥0,求a的范围。
9、(选做题)
A、B是曲线y=x3-ax上不同的两点,且过A、B两点的切线都与直线AB垂直。
(1)证明A、B两点关于原点对称 (2)证明|a|≥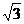
高三数学教学案
第二课时 导数的应用(一)
考纲摘录
1、理解运用导数的知识判断函数的单调性方法。
2、掌握运用导数的知识求函数的极值与最值的方法。
重点、难点
1、讨论含参数的函数的单调性。
2、理解极值、最值的概念,解决实际问题。
基础练习
1、f(x)=x4-2x2+1的单调增区间为________,单调减区间为________。
2、若函数f(x)=x3+ax-2在区间(1+∞)内是增函数,则实数a的取值范围( )
A (3,+∞) B [-3,+∞) C (-3,+∞) D(-∞,-3)
3、已知函数y=f(x)在x=1处的导数为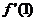 ,若f(1)为函数的极值,则( )
,若f(1)为函数的极值,则( )
A 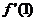 >0 B
>0 B
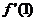 <0 C
<0 C 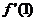 ≠0 D
≠0 D
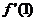 =0
=0
4、函数y=x3-3x2-9x+5在[-4,4]上的最大值为________。
5、函数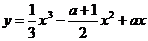 在(1,2)内是减函数,且在(2,+∞)内是增函数,则a=_____。
在(1,2)内是减函数,且在(2,+∞)内是增函数,则a=_____。
例题讲解
例1:已知f(x)=ax3+cx+d(a≠0)是R上奇函数,当x=1时,f(x)取得极值-2。
(1)求f(x)的单调区间和极大值
(2)证明对任意x1、x2∈(-1,1),不等式|f(x1)-f(x2)|<4恒成立
例2:已知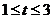 ,
,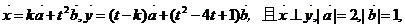
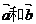 的夹角为600,求k的取值范围。
的夹角为600,求k的取值范围。
例3:一自来水厂的蓄水池中原有水650吨,一天24小时在向水池中注水的同时,蓄水池又向居民供水,若x小时内向居民的总供水量为240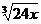 吨,问当每小时向水池注水120吨,一天中何时蓄水池中水量最少。
吨,问当每小时向水池注水120吨,一天中何时蓄水池中水量最少。
课后作业
班级_______学号__________姓名_________
1、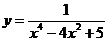 在区间(
在区间(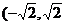 )内的单调性是________
)内的单调性是________
2、y=x4-4x3+1的极值是________
3、y=x4-32x+9在定义域R内的最小值为_________
4、若a<0,则函数f(x)=ax5-5ax在x=______处时取极小值________,在x=_______上时取极大值_______
5、y=-x3+mx2+1(m≠0)在(0,2)内的极大值为最大值,则m的取值范围是______
6、已知函数f(x)=x3+ax2+bx+c,在x=-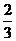 与x=1时f(x)都取得极值
与x=1时f(x)都取得极值
(1)求a、b的值
(2)若对x∈[-1,2]时,f(x)<c2值成立,求c的取值范围
7、已知二次函数f(x)当x=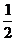 时有极值,函数图象过点(0,-1)点,且在该点处的切线与直线x-y=0垂直
时有极值,函数图象过点(0,-1)点,且在该点处的切线与直线x-y=0垂直
(1)求f(x)的解析式
(2)若g(x)=xf(x),求g(x)的单调递减区间
(3)设h(x)=(x+a)f(x),若对任意a∈[-1,1],h(x)在(-∞,m)和(n,+∞)上都是增函数,求m与n的取值范围。
8、某制药厂为了获得较大的收益,每年要投入一定的资金用于广告促销,经调查,当投入广告费为t(百万元)时(0≤t≤5)销售额约为-t2+5t(百万元)(注:收益=销售额-投入),若该厂准备投入3百万元,用于广告促销和技术改造,经预测,当投入技术改造费为x(百万元),销售额增加约为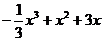 (百万元),请设计一个资金分配方案,使该厂由此获得的收益最大。
(百万元),请设计一个资金分配方案,使该厂由此获得的收益最大。
高三数学教学案
第三课时 导数的应用(二)
考纲摘录
导数与函数知识相结的综合运用,掌握用导数求函数的最大值、最小值问题,能利用函数的单调性证明或解不等式。
基础练习
1、三次函数y=x3-3bx+3b在[1,2]内恒成正值的充要条件( )
A 1≤b≤2 B
b≤0 C
1≤b≤2 D
b<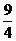
2、y=x3+3x2+6x-10切线中,斜率最小的切线方程是_______
3、直线y=a与函数f(x)=x3-3x的图象有三个不同的公共点,则a的取值范围是______
4、当正数k∈_______时,函数f(x)=kx3+3(k-1)x2-k2+1在(0,4)上是减函数。
例题讲解
例1:已知函数f(x)=-x3+ax2 +b(a、b∈k)
(1)要使f(x)在(0、1)上单调递增,求a的取值范围
(2)当a>0时,若函数满足y极小值=1,y极大值=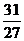 ,试求y=f(x)的解析式
,试求y=f(x)的解析式
(3)当x∈[0,1]时,y=f(x)图象上任意一点处的切线倾斜角为θ,求0≤θ≤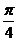 时,a的取值范围
时,a的取值范围
例2:设抛物线C1:y=x2-2x+2与C2:y=-x2+ax+b在它们同一个交点处的切线互相垂直。
(1)求a、b之间的关系
(2)若a>0,b>0,求ab的最大值
例3:f(x)=ax3+bx2+cx(a>0)的图象关于原点对称,A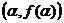 ,B
,B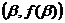 分别为函数的极大值点和极小值点,且|AB|=2,f(α)-f(β)= β-α.
分别为函数的极大值点和极小值点,且|AB|=2,f(α)-f(β)= β-α.
(1) 求b的值
(2)求f(x)的解析式
(3)求曲线y=f(x)与x2-y2=0的交点,并根据图形结构特点找出区间E=[m、n]使E={f(x)|x∈E}
课后作业
班级_______学号__________姓名_________
1、f(x)=ax3+bx2+cx+d(a>0),则f(x)为增函数的充要条件( )
A b2-4ac>0 B b>0,c>0 C b=0,c>0 D b2-3ac<0
2、设y=f(x)是二次函数,方程f(x)=0有两个相导实根且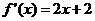 ,则y=f(x)的表达式_________。
,则y=f(x)的表达式_________。
3、若曲线C:y=x3-2ax2+2ax上任意点处的切线的倾角都是锐角,那以整数a的值等于_____。
4、已知f(x)=x3-x2+cx+d,若存在x1、x2,使a<x1<x2<b,且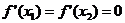 ,f(a)>f(x2),f(b)>f(x1),则f(x)在区间[a、b]上的最大值与最小值分别是(
)
,f(a)>f(x2),f(b)>f(x1),则f(x)在区间[a、b]上的最大值与最小值分别是(
)
A f(a),f(x1) B f(b),f(x2) C f(a),f(b) D f(x1),f(x2)
5、已知a为实数,f(x)=(x2-4)(x-a)
(1)求导数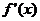
(2)求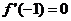 ,求f(x)在[-2,2]上的最大值和最小值
,求f(x)在[-2,2]上的最大值和最小值
(3)若f(x)在(-∞,-2]和[2,+∞)上都是递增的,求a的范围
6、已知f(x)=ax5-bx3+c在x=±1处有极大值为4,极小值为0,求a、b、c的值
7、f(x)=ax3+bx2+cx+d是定义在R上的函数,其图象交x轴于A、B、C三点,若B坐标(2,0),且f(x)在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上具有相反的单调性
(1)求C的值
(2)在函数图象上是否存在一点M(x0,y0),使得f(x)在点M的切线斜率为3b
(3)求|AC|的取值范围