
1、设集合U = {1,2,3,4,5},A =
{1,2,3},B = { 2,5}则A∩(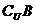 ) = ( )
) = ( )
A.{2} B.{2,3} C.{3} D.{1,3}
2、函数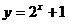 (
(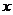 <1)的反函数是 ( )
<1)的反函数是 ( )
A.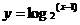
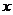 ∈(1,3) B.
∈(1,3) B.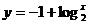
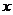 ∈(1,3)
∈(1,3)
C.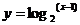
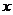 ∈(1,3] D.
∈(1,3] D.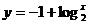
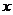 ∈(1,3]
∈(1,3]
3、如果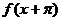 =
=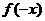 且
且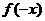 =
=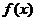 , 则
, 则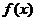 可以是 ( )
可以是 ( )
A.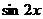 B.
B.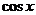 C.
C.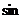 |
|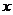 | D.|
| D.|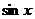 |
|
4、设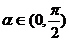 ,若
,若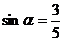 , 则
, 则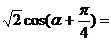 ( )
( )
A.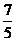 B.
B.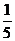 C.
C.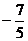 D.
D.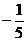
5、首项为
-24的等差数列,从第10项开始为正数,则公差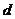 的取值范围是 ( )
的取值范围是 ( )
A.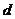 >
>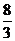 B.
B.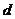 >3 C.
>3 C.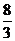 ≤
≤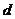 <3 D.
<3 D.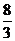 <
<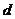 ≤3
≤3
6、设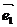 ,
,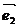 是两个不共线向量,若向量
是两个不共线向量,若向量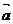 =3
=3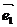 +5
+5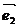 与向量
与向量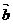 =
=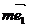 -3
-3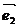 共线,则
共线,则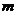 的值等于 ( )
的值等于 ( )
A.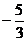 B.
B.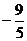 C.
C.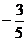 D.
D.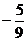
7、已知四边形ABCD中,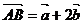 ,
,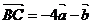 ,
,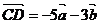 ,其中
,其中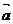 、
、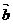 不共线,则四边形ABCD为 ( )
不共线,则四边形ABCD为 ( )
A.平行四边形 B.矩形 C.梯形 D.菱形
8、为了得到函数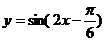 的图象,可以将函数
的图象,可以将函数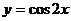 的图象 ( )
的图象 ( )
A.向右平移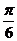 个单位 B.向右平移
个单位 B.向右平移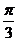 个单位
个单位
C.向左平移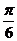 个单位 D.向左平移
个单位 D.向左平移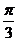 个单位
个单位
9、等差数列{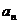 }中,
}中,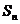 是前
是前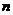 项和,且
项和,且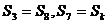 ,则
,则 的值为 ( )
的值为 ( )
A.4 B.11 C.2 D.12
10、已知函数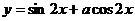 的图象关于直线
的图象关于直线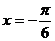 对称,则函数
对称,则函数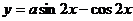 的图象关于下列各点中对称的是 ( )
的图象关于下列各点中对称的是 ( )
A.(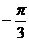 ,0) B.(-
,0) B.(-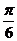 ,0) C.(
,0) C.(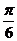 ,0) D.(
,0) D.(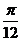 ,0)
,0)
11、在△ABC中,如果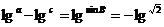 ,并且B为锐角,则△ABC的形状是( )
,并且B为锐角,则△ABC的形状是( )
A.等边三角形 B.直角三角形 C.等腰三角形 D.等腰直角三角形
12、已知线段PQ=a,A1是线段PQ的中点,A2是QA1的中点,A3是A1A2的中点,A4是A3A2的中点,……An是An-2An-1的中点,则PAn长为 ( )
A.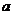 .
. B.
B. 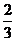
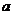 .
.
C. 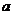 .
.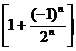 D.
D.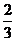
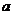 .
.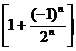
13、若函数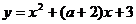
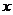
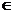 [
[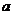 ,
,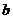 ]的图象关于直线
]的图象关于直线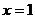 对称,则
对称,则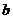 =________.
=________.
14、函数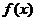 是奇函数,当
是奇函数,当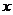 >0时,
>0时,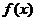 =
=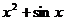 ,当
,当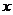 <0时,
<0时,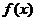 的表达式为________.
的表达式为________.
15、求值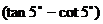 .
.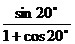 =___________.
=___________.
16、已知向量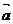 、
、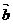 满足|
满足|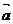 |=2,|
|=2,|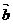 |=1,|
|=1,|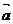 -
-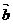 |
=2,则|
|
=2,则|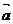 +
+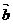 | =___________.
| =___________.
17、数列{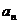 }是等差数列S9=18,Sn=240,an-4=30(n>9) 则n的值为___________.
}是等差数列S9=18,Sn=240,an-4=30(n>9) 则n的值为___________.
18、设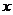 、
、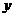 ∈[
∈[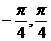 ]
] 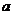 ∈R,且
∈R,且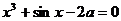 ,
,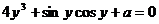 ,则
,则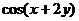 =___________.
=___________.
13、_________________. 14、_________________.
15、_________________. 16、_________________.
17、_________________. 18、_________________.
19、(本小题满分12分)
已知函数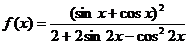
(1)求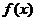 的定义域和值域;
的定义域和值域;
(2)求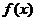 的最小正周期及单调递增区间.
的最小正周期及单调递增区间.
20、(本小题满分12分)
已知函数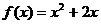 .
.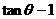 ,
,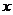 ∈[-1,
∈[-1,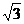 ],其中
],其中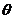
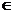 (
( 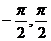 )
)
(1)当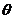 =
=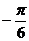 时,求函数
时,求函数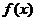 的最大值与最小值;
的最大值与最小值;
(2)求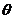 的取值范围,使
的取值范围,使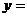
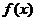 在区间[-1,
在区间[-1,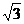 ]上是单调函数.
]上是单调函数.
21、(本小题满分14分)
已知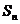 是等比数列{
是等比数列{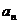 }的前
}的前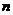 项的和,
项的和,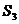 ,
,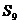 ,
,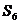 成等差数列.
成等差数列.
(1)求数列{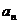 }的公比
}的公比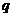
(2)试问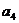 ,
,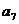 的等差中项是数列{
的等差中项是数列{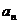 }中的第几项?请说明理由.
}中的第几项?请说明理由.
22、(本小题满分14分)
已知函数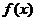 =
=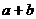 .
.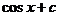 .
.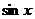 的图象经过(0,1),(
的图象经过(0,1),(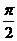 ,1)且当0≤
,1)且当0≤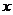 ≤
≤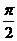 时,恒有|
时,恒有|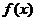 |≤2,
|≤2,
(1)求实数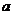 的取值范围.
的取值范围.
(2)当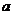 取上述范围内的最大整数值时,若有实数
取上述范围内的最大整数值时,若有实数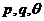 使
使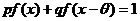 对一切实数
对一切实数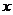 恒成立,试求
恒成立,试求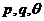 的值.
的值.
23、(本小题满分14分)
已知函数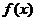 =
=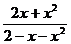 (0<
(0<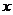 <1)的反函数为
<1)的反函数为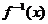
(1)已知数列{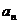 }满足
}满足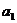 =1,
=1,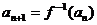 ,(
,(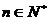 )
)
求数列{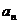 }的通项公式
}的通项公式
(2)已知数列{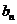 }满足
}满足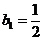 ,
,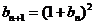 .
.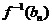 ,(
,(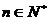 )
)
求证:对一切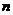 ≥2的正整数,都满足:1<
≥2的正整数,都满足:1<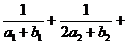 ……
…… <2
<2