1.
求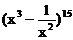
的展开式中的常数项。[-5005]
2.
求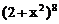
的展开式中
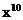的系数。[448]
3.
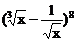的展开式中，x的一次项的系数是___________。[28]
4.
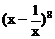的展开式中，
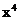的系数与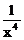
的系数之差是_________。[0]
5.
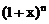的展开式中，若第三项与第六项的系数相等，则
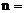_____。[7]
6.
在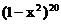
的展开式中，如果第4r项和第
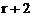项的二项式系数相等，(1)求r的值；(2)写出展开式中的第4r项和第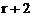项。[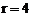
；
，
]
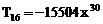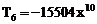7.
已知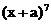
的展开式中，
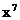的系数是
，则实数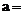
__________。[
]
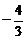8.
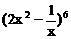的展开式中的常数项为______________。[60]
9.
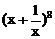的展开式中
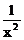的系数是_______________。[56]
10.
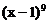按x降幂排列的展开式中，系数最大的项是( )(A)第4项和第5项(B)第5项(C)第5项和第6项(D)第6项[B]
11.
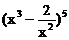的展开式中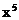
的系数是_______________。[40]
12.
若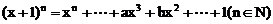
，且
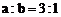，那么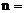_______。[11]
13.
在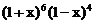
的展开式中，
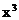的系数是__________。[-8]
14.
若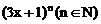
的展开式中各项系数的和是256，则展开式中
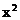的系数是__________。[54]
15.
设n是一个自然数，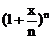
的展开式中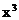的系数为
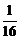，则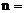______。[4]
16.
在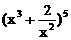
的展开式中，含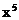项的系数为_______________。[40]
17.
若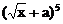
的展开式中的第四项是
(a是大于零的常数)，则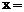
__________。[
]
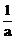18.
在二项式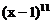
的展开式中，系数最小的项的系数为____________。[-462]
19.
二项式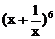
的展开式中的常数项的值______________。[20]
20.
在代数式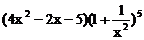
的展开式中，常数项为___________。[15]
21.
若在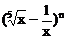
的展开式中，第4项是常数项，则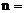_________。[18]
22.
在二项式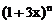
和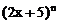
的展开式中，各项系数之和分别记为
、
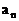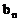，n是正整数，则
_____________。[
]
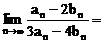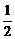23. 已知数列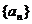
(n为正整数)是首项是a1，公比为q的等比数列，(1)求和：
，
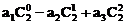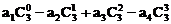；(2)由(1)的结果归纳概括出关于正整数n的一个结论，并加以证明。[(1)
；
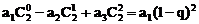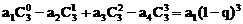；(2)归纳概括的结论为：若数列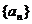是首项为a1，公比为q的等比数列，则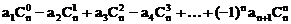
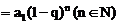，证明略]
24.
如图，在由二项式系数所构成的杨辉三角形中，第_____行中从左至右第14与第15个数的比为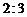
。[34]
25.
若在二项式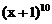
的展开式中任取一项，则该项的系数为奇数的概率是_____________。[
]
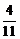26.
若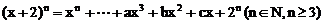
，且
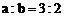，则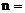
___________。[11]
27.
在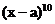
的展开式中，
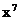的系数是15，则实数__________。[
]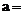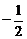