
2、简单的高次不等式与分式不等式的解法
3、二次不等式解集与二次方程以及二次函数之间的关系
基本方法:分类讨论,数形结合,函数与方程、等价转化的思想
重点难点
重点:一元二次不等式的基本解法。
难点:讨论一元二次不等式系数中的字母取值问题。
基础练习
1.① 不等式ax>b的解集是:
②一元二次不等式ax2+bx+c>0(a>0)的解集是:
2.已知关于x的不等式:(a+b)x+(2a-3b)<0的解集为(-∞,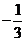 )。则关于x的不等式(a-3b)x+(b-2a)>0的解集为
。
)。则关于x的不等式(a-3b)x+(b-2a)>0的解集为
。
3.已知不等式ax2-5x+b>0的解集为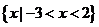 ,则不等式bx2-5x+a>0的解集为
。
,则不等式bx2-5x+a>0的解集为
。
4.若不等式(a-2)x2+2(a-2)x-4<0对x∈R恒成立,则a的取值范围是 ( )
A.(-∞,2] B.(-2,2] C.(-2,2 ) D.(-∞,-2)
5.下列各组不等式中,解集完全相同的是 ( D )
A.x2-4x<6与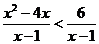 B.
B.
C.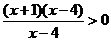 与x+1>0 D.
与x+1>0 D.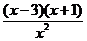 >0与
>0与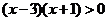
例题讲解
例1.解下列关于x的不等式:
(1)(x+2)(x+1)2(x-1)(x-2)
≤0 ;
(2) 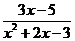 ≤2 ;
≤2 ;
(3) ax2-(a+1)x+1<0 ; (4)3x2-mx-m>0。
例2.设不等式组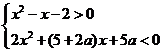 的整数解只有-2。求实数a的取值范围。
的整数解只有-2。求实数a的取值范围。
例3.关于x的不等式x2-(a+a2)x+a3<0
(1) 若其解集是(2,4),求a的值;
(2) 若该不等式在 (2,4)上恒成立,求a的取值范围。
例4.设集合M=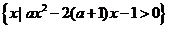 ,已知M≠φ,M
,已知M≠φ,M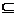 R+。求a的取值范围。
R+。求a的取值范围。
课后作业
班级 学号 姓名
1.不等式x+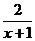 >2的解集是
。
>2的解集是
。
2.已知关于x的不等式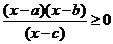 的解集为[-1,2) ∪[3,+ ∞),则不等式
的解集为[-1,2) ∪[3,+ ∞),则不等式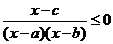 的解集为
。
的解集为
。
3.设f(x)和g(x)都是定义域为R的奇函数,不等式f(x)>0的解集为(m,n),不等式g(x)>0的解集为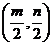 ,其中0<m<
,其中0<m<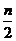 ,则不等式f(x)g(x)>的解集是 。
,则不等式f(x)g(x)>的解集是 。
4.设不等式x2-4mx+4m2+m+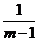 >0的解集为R,则m的取值范围是
。
>0的解集为R,则m的取值范围是
。
5.当不等式2≤x2+px+10≤6中恰有一个解时,实数p的值是 ( )
A.2 B.-2 C.2或-2 D.4或-4
6.已知不等式ax2-bx+c>0的解集是( ,2)。对于a、b、c有以下结论:(1)a>0;(2)b>0;(3)c>0;(4)a+b+c>0;(5)a-b+c>0。其中正确结论的序号是
,2)。对于a、b、c有以下结论:(1)a>0;(2)b>0;(3)c>0;(4)a+b+c>0;(5)a-b+c>0。其中正确结论的序号是
7.解下列不等式(组):
(1)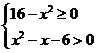 ;
(2)
;
(2)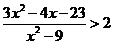 ;
;
(3)1+x-x3-x4<0 ;
(4)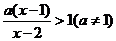
8.已知不等式组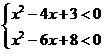 的解集是不等式2x2-9x+a<0的解集的子集,求实数a的取值范围。
的解集是不等式2x2-9x+a<0的解集的子集,求实数a的取值范围。
9.关于x的不等式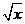 >ax+
>ax+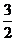 的解集为(4,b),求a,b的值。
的解集为(4,b),求a,b的值。
10.已知cos2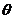 +msin
+msin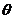 -2>0在
-2>0在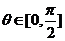 上恒成立,求m的取值范围。
上恒成立,求m的取值范围。
 第六章 不等式
第六章 不等式
班级 学号 姓名
第八课时 含有绝对值的不等式
考纲摘录
1. 理解绝对值的含义
2. 理解绝对值不等式的性质:|a|-|b|≤|a±b|≤|a|+|b|,弄清其中等号成立的条件。
3. 掌握简单的含绝对值不等式的解法。
知识概要
知识点:1.掌握两类最简的绝对值不等式:10|f(x)| ≥a (a>0)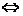 f(x)≤-a或f(x)≥a;
f(x)≤-a或f(x)≥a;
20 |f(x)|
≤a (a>0) 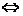 -a≤f(x)≤a
-a≤f(x)≤a
2.能够利用绝对值的几何意义和平方法解含有绝对值的不等式
3.能利用讨论的方法解含有多个绝对值的不等式
4.应用绝对值不等式的性质对不等式进行放和缩,并能对不等式进行证明。
基本方法:分类讨论、数形结合、平方法
重点难点
重点:含绝对值不等式的解法
难点:绝对值不等式的性质的运用以及含参数的一些绝对值不等式的讨论。
基础练习
1.不等式1≤|2x-1|<2的解集为 。
2.已知不等式|x-m|<1成立的充分不必要条件是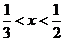 。则实数m的取值范围是
( )
。则实数m的取值范围是
( )
A .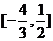
 B.
B.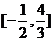 C.
C.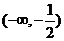 D.
D.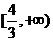
3.对于|a|-|b|≤|a+b|≤|a|+|b|,下列结论中,正确的是 ( )
A.a,b异号时,左边等号成立 B.a,b同号时,右边等号成立
C.a+b=0时,等号两边均成立 D.a+b>0时,右边等号成立;当a+b<0时,左边等号成立
4.若a,b∈R,且|a-c|<|b|,则 ( )
A.|a|<|b|+|c| B.|a|>|b|-|c| C.a<b+c D.a>b-c
5.若不等式|x-4|+|x-3|<a的解集非空,则实数a的取值范围是 。
例题讲解
例1.解下列关于x不等式:
(1)|x-x2-2|>x2-3x-4;
(2)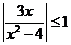
(3)| |x+3|-|2x-1|>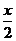 +1
(4)|ax-1|<3 ;
+1
(4)|ax-1|<3 ;
例2、已知不等式x+|x-2c|>1的解集为R,求实数c的取值范围。
例3.若t>0,且|x-1|<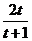 ,求证:
,求证: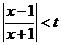 。
。
例4.设f(x)=ax2+bx+c(a≠0),当|x|≤1,总有|f(x)|≤1,求证:|f(2)| ≤8。
课后作业:
1.不等式(1+x)(1-|x|)>0的解集是 。
2.不等式|x+2|≥|x|的解集是 。
3.对任意实数x,若不等式|x-5|-|x+2|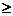 k恒成立,则k的取值范围是
。
k恒成立,则k的取值范围是
。
4.若m>0,则|x-a|<m和|y-a|<m是|x-y|<2m的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
5.已知函数f(x),g(x),定义域为R.设不等式|f(x)|+|g(x)|<a (a>0)的解集为M,不等式|f(x)+g(x)|<a(a>0)的解集为N,则M和N的关系为 ( )
A.N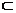 M
B.M=N
C.M
M
B.M=N
C.M 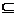 N
D.M
N
D.M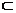 N
N
6.若不等式x2-a|x|+2≥0对一切负实数x恒成立,则a的取值范围 。
7.解下列不等式:
(1)|x2-11x+21|>x ; (2)|x2-4|+|x+3|>5
(3)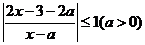 (4)x|x-a|
(4)x|x-a|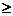 2a2 (a<0)
2a2 (a<0)
8.若⑴ |x-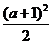 |≤
|≤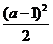 与 ⑵ x2-3(a+1)x+2(3a+1) ≤0(a∈R)的解集依次记为A与B,求使得A
与 ⑵ x2-3(a+1)x+2(3a+1) ≤0(a∈R)的解集依次记为A与B,求使得A B的a的取值范围。
B的a的取值范围。
9.已知适合不等式|x2-4x+p|+|x-3|≤5的x的最大值为3。
(1)求p的值;
(2)若f-1(x)=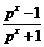 ,k>0,解关于x的不等式f-1(x)>logp
,k>0,解关于x的不等式f-1(x)>logp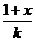 。
。
10.(选做题)设a,b,c∈R,若函数f(x)=ax2+bx+c,g(x)=cx2+bx+a,且当|x|≤1时,|f(x)| ≤2.
(1)求证:|g(1)| ≤2;
(2)求证:|x|≤1时,|g(x)| ≤4