
1、了解随机事件、必然事件、不可能事件的概念。
2、掌握等可能性事件的概率公式P(A)=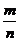 。
。
3、能熟练地运用排列组合的知识解决等可能性事件的概率问题。
重点、难点
1、用等可能性事件的概率公式P(A)=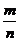 解题时,一定先弄清该事件的“一次试验”是什么,再看确定的基本事件相互间是否等可能性。
解题时,一定先弄清该事件的“一次试验”是什么,再看确定的基本事件相互间是否等可能性。
2、 解题过程中要把握一些关键词,如“有序”与“无序”,“放回”与“不放回”,“至
少”与“恰好”等。
基础练习
1、 从含有 500个个体的总体中一次性抽取25个个体,假定其中每个个体被抽到的概率相等,那么总体中的每个个体被抽到的概率等于____________。
2、从甲、乙、丙三人中任选两名代表,甲被选中的概率是_________。
3、从长度分别为1,3,5,7,9个单位的5条线段中,任取3条作边,能构成三角形的概率为__________。
4、在10张奖券中,有4张有奖,从中任抽两张,能中奖的概率为( )
A 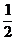 B
B
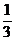 C
C
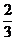 D
D
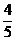
5、若以连续掷两次骰子分别得到的点数m、n作为点P的坐标(m,n),则点P落在圆x2+y2=16内的概率是________。
例题讲解
例1、袋中有红、黄、白色球各一个,每次任取一个,有放回地抽三次,计算下列事件的概率:
(1)三次颜色各不相同;
(2)三次颜色不全相同;
(3)三次取出的球无红色或无黄色。
例2、由1,2,3,4,5组成一个无重复数字的五位数。
计算:(1)这个五位数能被2整除的概率;
(2)这个五位数能被3整除的概率;
(3)这个五位数比45000大的概率。
例3、设有n个人,每个人都等可能地被分配到N个房间的任意一间去住(n≤N),求下列事件的概率:
(1)指定的n个房间各有一个人住;
(2)恰有n个房间,其中各住一个人;
(3)某指定房间中含有m(m≤n)个人住。
课后作业
班级_______学号__________姓名_________
1、从1,2,3,……,100这些正整数中任取一个数,那么所抽得的数恰好是7的倍数的概率是_______。
2、同时掷两颗不同的骰子,求所得的点数之和为6的概率为______。
3、有2n个数字,其中一半是奇数,一半是偶数,从中任取两个数,则所得的两数之和为偶数的概率为( )
A 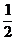 B
B
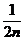 C
C
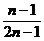 D
D
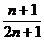
4、有5个人随意排成一排,其中甲不在左端,且乙在中间的概率为_________。
5、某人有五把钥匙,其中有一把是开办公桌的抽屉锁的,但他忘了是哪一把,于是他便将五把钥匙逐把不重复地试开,恰好第三次打开抽屉锁的概率是_______。
6、袋中装有大小相同的分别写有1,2,3,4,5的五个小球,求下列事件的概率:
(1)从中任取三球,其中有写有1的小球;
(2)从中每次任取一球,记下号码后放回,这样连续取三次,其中有写有1的小球。
7、从0,1,2,…,9这十个数字中,任取不同的三个数字,求三个数字之和等于10的概率。
8、现有10张奖券,其中两张有奖,甲、乙、丙依次各抽一张,求:(1)乙中奖的概率;(2)三人中恰有一人中奖的概率。
9、已知8支球队中有3支弱队,以抽签方式,将这支球队分为A、B两组,每组4支,求:(1)A、B组中有一组恰有两支弱队的概率;(2)A组中至少有两支弱队的概率。
高三数学教学案 第十章 排列、组合与概率
第八课时 互斥事件有一个发生的概率
考纲摘录
1、理解互斥事件与对立事件的概念。
2、能熟练运用互斥和对立事件的概率公式解题。
知识概要
1、互斥事件的概率公式:P(A+B)=P(A)+P(B)
2、对立事件的概率公式:P(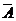 )=
)=
重点、难点
1、对立事件必是互斥事件,反之未必成立。
2、在一个试验中,常需将较复杂的事件分解成几个较简单的互斥事件的和,或借助其对立事件来把握该事件。
基础练习
1、从1,2,3,…9这9个自然数中任取两个数,分别有下列事件;(1)恰有一个奇数和恰有一个偶数;(2)至少有一个奇数和两个都是偶数;(3)两个都是奇数和两个都是偶数;(4)至少有一个奇数和至少有一个偶数,其中为互斥事件的是( )
A (1) B (2)(4) C (2)(3) D (3)
2、掷一颗骰子,设A为“出现2点”,B为“出现奇数点”,则P(A+B)等于______。
3、某射手在一次射击命中9环的概率为0.28,命中8环的概率为0.19,不够8环的概率为0.29,这个射手在一次射击命中9环或10环的概率为_________。
4、从1,2,3,…,10这十个数字中任取两个数相乘,积是3的倍数的概率为_____。
5、如果在100张有奖储蓄的奖券中,只有一、二、三等奖,其中一等奖1个,二等奖5个,三等奖10个,那么买一张奖券,中奖的概率为( )
A 0.10 B 0.12 C 0.16 D 0.18
例题讲解
例1、有100个产品,其中一等品60个,二等品30个,三等品10个,现任取2个,求取出产品中至多有一个一等品的概率。
例2、袋中有5个白球,3个黑球,从中任意摸出4个,求下列事件发生的概率。
(1)摸出2个或3个白球;
(2)至少摸出1个白球;
(3)至少摸出1个黑球.
例3、从男女学生共36名的班级中,任意选出2名委员,任何人都有同样的当选机会,如果选得同性别委员的概率是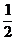 ,求男女相差几名?
,求男女相差几名?
课后作业
班级_______学号__________姓名_________
1、从2件一等品和2件二等品中任取2件,是对立事件的为( )
A 至少有1件二等品与全是二等品
B 至少有1件一等品与至少有1件二等品
C 恰有1件二等品与恰有2件二等品
D 至少有1件二等品与全是一等品
2、从5名礼仪小姐、4名翻译中任选5人参加一次经贸洽谈活动,其中礼仪小姐、翻译均不少于2人的概率是_______。
3、由数字1,2,3组成可重复数字的三位数,则三位数中至多出现两个不同数字的概率为_________。
4、口袋中有10个相同的球,其中5个标有0,5个标有1,若从袋中摸出5个球,则摸出的5个球所标数字之和小于2或大于3的概率是_______。
5、甲袋中装有m个白球,n个黑球;乙袋中装有n个白球,m个黑球(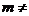 n),现从两袋中各摸一个球,A:“两球同色”,B:“两球异色”,则P(A)与P(B)的大小关系为
n),现从两袋中各摸一个球,A:“两球同色”,B:“两球异色”,则P(A)与P(B)的大小关系为
( )
A P(A)< P(B) B P(A)= P(B)
C P(A)> P(B) D 视m,n大小而定
6、袋中放有3个伍分硬币,3个贰分硬币和4个壹分硬币,从中任取3个,求面值和超过8分的概率。
7、有A、B两个口袋,A袋中有4个白球和2个黑球,B袋中有3个白球和4个黑球,从A、B袋中各取两个球交换后,求A袋中仍装有4个白球的概率。
8、某班有6位同学是1986年9月份出生的,求这6位同学中至少有两人是同一天出生的概率。(本题只要求列式)
9、(选做题)从一副52张的扑克牌中任取4张,求其中至少有2张花色相同的概率。(本题只要求列式)