
1、掌握二项式定理及其展开式的通项公式;
2、会运用通项公式求解二项展开式中某些特定项及其系数.
知识概要
1、二项式定理: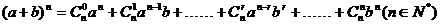 ;
;
2、通项公式: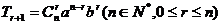 表示二项展开式中的第
表示二项展开式中的第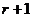 项,
项,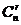 叫做展开式中第
叫做展开式中第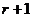 项的二项式系数.
项的二项式系数.
重点难点
1、二项式系数与项的系数的区别;
2、灵活运用通项公式(其中 如果是未知量,常常要用方程(组)求解).
如果是未知量,常常要用方程(组)求解).
基础练习
1、若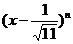 的展开式中,第三项系数等于6,则等于 ( )
的展开式中,第三项系数等于6,则等于 ( )
A.4 B.8 C.12 D.16
2、对于二项式 四位同学作出了四种判断:
四位同学作出了四种判断:
①存在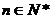 ,展开式中有常数项;
,展开式中有常数项;
②对于任意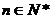 ,展开式中没有常数项;
,展开式中没有常数项;
③对于任意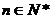 ,展开式中没有
,展开式中没有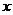 的一次项;
的一次项;
④存在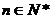 ,展开式中有
,展开式中有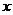 的一次项.
的一次项.
上述判断中正确的是 ( )
A.①与③ B.②与③ C.②与④ D.④与①
3、 的展开式中
的展开式中 的系数是 ( )
的系数是 ( )
A.1260 B.126 C.1296 D.3024
4、在 展开式中,有理式的项数为 ( )
展开式中,有理式的项数为 ( )
A.1 B.2 C.3 D.4
5、设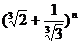 展开式的第7项与倒数第7项的比是1:6,则展开式中的第7项为________.
展开式的第7项与倒数第7项的比是1:6,则展开式中的第7项为________.
6、二项式 展开式中,若相邻两项的系数之比为8:15,则
展开式中,若相邻两项的系数之比为8:15,则 的最小值为_______.
的最小值为_______.
7、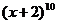 .
. 展开式中
展开式中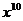 的系数为_______.
的系数为_______.
8、 展开式中第5项与第11项的二项展开式系数相等,则
展开式中第5项与第11项的二项展开式系数相等,则 =________.
=________.
例题讲解
例1、(1)已知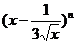 的展开式中,第三项系数为4,求它的常数项.
的展开式中,第三项系数为4,求它的常数项.
(2)求 展开式中的常数项(答案可保留组合数).
展开式中的常数项(答案可保留组合数).
例2、若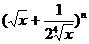 展开式中前三项系数成等差数列,求:
展开式中前三项系数成等差数列,求:
(1)展开式中含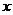 的一项幂的项;
的一项幂的项;
(2)展开式中所有含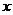 的有理项;
的有理项;
(3)展开式中系数最大的项.
课后作业
班级_______学号__________姓名_________
1、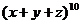 的展开式中含
的展开式中含 项的系数为 ( )
项的系数为 ( )
A.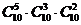 B.
B.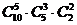 C.
C.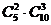 D.
D.
2、在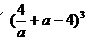 的展开式中,常数项的值是_________.
的展开式中,常数项的值是_________.
3、二项式 的展开式中第21项和第22项相等,则非零实数
的展开式中第21项和第22项相等,则非零实数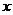 等于_________.
等于_________.
4、 的展开式中有且仅有五个有理项,则最小自然数
的展开式中有且仅有五个有理项,则最小自然数 等于_______.
等于_______.
5、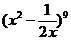 展开式中
展开式中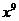 的系数是_______.
的系数是_______.
6、设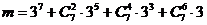 ,
,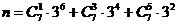 ,则
,则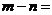 _______.
_______.
7、若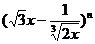 的展开式中含有常数项,求这样的正整数
的展开式中含有常数项,求这样的正整数 的最小值.
的最小值.
8、在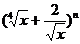 的展开式中,已知最后三项的系数成等差数列,求这个展开式中所有的有理项.
的展开式中,已知最后三项的系数成等差数列,求这个展开式中所有的有理项.
9、(选做题)
已知数列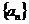 的通项公式为
的通项公式为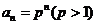 ,其前
,其前 项和为
项和为 ,且对任意
,且对任意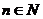 *都有
*都有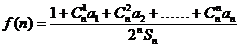 试比较
试比较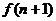 与
与 的大小.
的大小.
高三数学教学案 第十章 排列、组合、二项式定理
第五课时 二项式定理及其应用(一)
考纲摘录
1、能利用二项式系数的性质求多项式系数的和,求一些组合数的和;
2、能熟练地逆向运用二项式定理求和.
知识概要
1、二项式系数的对称性;
2、二项式系数的大小规律;
3、二项式系数的和.
基础练习
1、 等于 ( )
等于 ( )
A.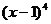 B.
B. C.
C.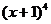 D.
D.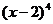
2、在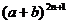 的展开式中,二项式系数最大的项是 ( )
的展开式中,二项式系数最大的项是 ( )
A.第 项 B.第
项 B.第 项和第
项和第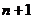 项 C.第
项 C.第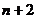 项 D.第
项 D.第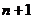 项和第
项和第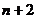 项
项
3、若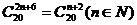 且
且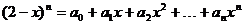 ,则
,则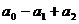

 等于 ( )
等于 ( )
A.81 B.27 C.243 D.729
4、已知 展开式中常数项为1120,其中实数
展开式中常数项为1120,其中实数 是常数,则展开式中各项系数的和是
是常数,则展开式中各项系数的和是
( )
A.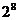 B.
B.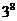 C.1或
C.1或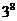 D.1或
D.1或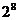
5、如果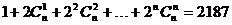 ,则
,则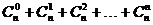 =________.
=________.
6、在 为正整数
为正整数 的二项展开式中,奇数项的和为P,偶数项的和为Q,则
的二项展开式中,奇数项的和为P,偶数项的和为Q,则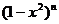 的值为_______.
的值为_______.
例题讲解
例1、已知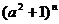 展开式中的各项系数之和等于
展开式中的各项系数之和等于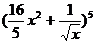 的展开式的常数项,而
的展开式的常数项,而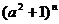 的展开式的系数最大的项等于54,求
的展开式的系数最大的项等于54,求 的值.
的值.
例2、已知 展开式中各项的系数和比各项的二项式系数和大992,求展开式中系数最大的项.
展开式中各项的系数和比各项的二项式系数和大992,求展开式中系数最大的项.
例3、设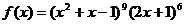 ,试求
,试求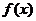 的展开式中
的展开式中
(1)所有项的系数和;
(2)所有偶次项的系数和及所有奇次项的系数和.
例4、已知 的展开式中
的展开式中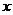 项的系数为11
项的系数为11
(1)求展开式中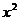 项系数的最小值;
项系数的最小值;
(2)当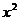 项系数取最小值时,求
项系数取最小值时,求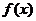 展开式中
展开式中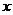 的奇次幂项的系数之和.
的奇次幂项的系数之和.
课后作业
班级_______学号__________姓名_________
1、已知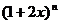 的展开式中所有系数之和等于729,那么这个展开式中第四项的系数为
的展开式中所有系数之和等于729,那么这个展开式中第四项的系数为
( )A.20 B.160 C.180 D.240
2、在 的展开式中,
的展开式中, 的系数是通项公式
的系数是通项公式 的数列的
的数列的
( )
A.第20项 B.第18项 C.第11项 D.第3项
3、设二项式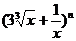 的展开式的各项系数的和为P,所有二项式系数的和为S,若有P+S=272,则
的展开式的各项系数的和为P,所有二项式系数的和为S,若有P+S=272,则 _________.
_________.
4、如果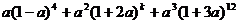 的展开式中含
的展开式中含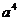 项的系数为144,则正整数
项的系数为144,则正整数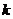 的值为_______.
的值为_______.
5、已知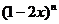 的展开式中,奇数项的二项式系数之和为32,则该二项展开式的中间项为_______.
的展开式中,奇数项的二项式系数之和为32,则该二项展开式的中间项为_______.
6、若二项式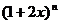 的展开式中第6项与第7项的系数相等,求展开式中二项式系数最大的项和系数最大的项.
的展开式中第6项与第7项的系数相等,求展开式中二项式系数最大的项和系数最大的项.
7、求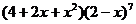 的展开式中
的展开式中 的系数.
的系数.
8、已知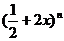 .
.
(1)展开式中第五、第六、第七项的二项式系数成等差数列,求展开式中二项式系数最大的项的系数;
(2)若展开式中前三项的二项式系数之和等于79,求展开式中系数最大的项.
高三数学教学案 第十章 排列、组合、二项式定理
第六课时 二项式定理及其应用(二)
考纲摘录
能利用二项式定理进行计算和证明一些简单问题.
知识概要 二次项定理的主要应用
(1)赋值求值 (2)证明某些整除问题或求余数
(3)证明有关等式及不等式 (4)进行近似计算.
基础练习
1、在 )的展开式中,含
)的展开式中,含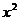 项的系数为 ( )
项的系数为 ( )
A. B.
B.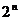 C.
C.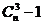 D.
D.
2、若 ,则
,则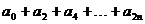 的值等于 ( )
的值等于 ( )
A. B.
B.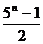 C.
C.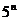 D.1
D.1
3、若 ,则
,则 等于
等于
( )
A.14 B.12 C.10 D.8
4、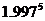 精确到0.001的近似值为________.
精确到0.001的近似值为________.
5、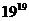 除以5的余数为________.
除以5的余数为________.
6、若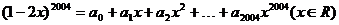 ,则
,则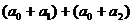 +
+
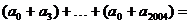 ________.
________.
例题讲解
例1、设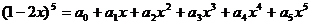 ,求
,求
(1) 的值;
的值;
(2)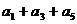 的值;
的值;
(3)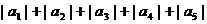 的值.
的值.
例2、求证: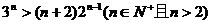 .
.
例3、(1)若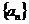 是首项为
是首项为 ,公比为
,公比为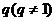 的等比数列,求和:
的等比数列,求和: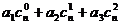
 ;
;
(2)若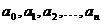 为等差数列,求证:
为等差数列,求证: .
.
例4、设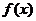 是定义在R上的一个给定的函数,函数
是定义在R上的一个给定的函数,函数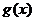
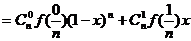

(1)若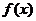 =1恒成立,求
=1恒成立,求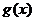 ;
;
(2)当 时,求
时,求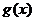 .
.
课后作业
班级_______学号__________姓名_________
1、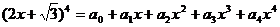 ,则
,则 的值为
的值为
( )A.1 B.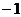 C.0 D.2
C.0 D.2
2、若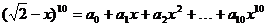 ,则
,则
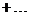
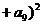 的值为_______.
的值为_______.
3、设 为奇数,则
为奇数,则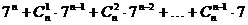 被9除的余数是_________.
被9除的余数是_________.
4、 除以100的余数是_______.
除以100的余数是_______.
5、计算 精确到1的近似值为(
)
精确到1的近似值为(
)
A.99000 B.99002 C.99004 D.99005
6、设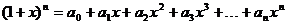 ,若
,若 ,则
,则 =_________.
=_________.
7、 ,则
,则
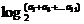 =__________.
=__________.
8、求证: 能被64整除,其中
能被64整除,其中 为非负整数.
为非负整数.
9、设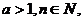 且
且 ≥2,求证:
≥2,求证: .
.
10、选做题
已知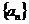 (
( 为正整数)是首项为
为正整数)是首项为 ,公比为
,公比为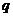 的等比数列;
的等比数列;
(1)求和: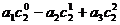 ,
, ;
;
(2)由(1)的结果归纳概括出关于正整数 的一个结论,并加以证明;
的一个结论,并加以证明;
(3)设 ,
, 是等比数列
是等比数列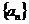 的前n项和,求:
的前n项和,求: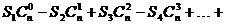
 .
.