
1、理解直线的倾斜角和斜率的概念,掌握过两点的直线的斜率公式;
2、掌握直线方程的几种形式,并能根据条件熟练地求出直线的方程;
知识概要
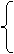 直线特征量(倾斜角、斜率、截矩、方向向量)
直线特征量(倾斜角、斜率、截矩、方向向量)
知识点 两点间连线的斜率公式
直线方程的基本形式(点斜式,斜截式、两点式、截矩式、一般式)
重点、难点
重点:求直线的特征量及直线方程
难点:直线斜率、倾斜角范围问题,待定系数法求直线方程
基础练习
1、判断下列命题的正误:
(1)任何一条直线都有倾斜角,也都有斜率; ( )
(2)直线的倾斜角的范围是[0,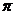 ); ( )
); ( )
(3)直线斜率的范围是(-∞,+∞); ( )
(4)两条直线的斜率相等,则它们的倾斜角相等 ( )
2、经过点(2,1),且方向向量为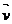 =(
=(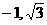 )的直线
)的直线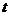 的点斜式方程是____________,斜截式方程是____________;倾斜角是____________;经过两点(
的点斜式方程是____________,斜截式方程是____________;倾斜角是____________;经过两点(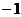 ,8)和(4,
,8)和(4,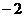 )的直线
)的直线 的两点式方程是____________,截矩式方程是_________,一般式方程是__________.
的两点式方程是____________,截矩式方程是_________,一般式方程是__________.
3、过点A(3,2),且在两坐标轴上截矩相等的直线方程是____________.
4、设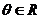 ,则直线
,则直线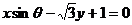 的倾斜角的取值范围是____________.
的倾斜角的取值范围是____________.
例题讲解
例1、已知直线 过点A(2,1),B(
过点A(2,1),B(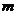 ,2).
,2).
(1)求直线 的方程.
的方程.
(2)求 的倾斜角
的倾斜角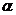 的取值范围.
的取值范围.
例2、经过点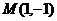 的直线
的直线 分别与直线
分别与直线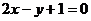 和
和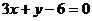 相交于
相交于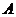 、
、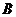 两点,若
两点,若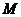 分
分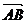 之比为2:1,求直线
之比为2:1,求直线 的方程.
的方程.
例3、过点P(2,1)作直线 交
交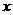 、
、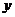 轴正半轴于A、B两点,当|PA|.|PB|取到最小值时,求直线
轴正半轴于A、B两点,当|PA|.|PB|取到最小值时,求直线 的方程.
的方程.
课后作业
班级_______学号__________姓名_________
1、直线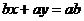 (
(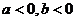 )的倾斜角是___________.
)的倾斜角是___________.
2、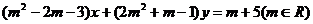 是直线
是直线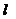 方程,其倾斜角为
方程,其倾斜角为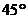 ,则实数
,则实数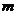 的值为__________.
的值为__________.
3、直线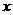 .
.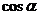 +
+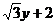 =0的倾斜角范围是____________.
=0的倾斜角范围是____________.
4、过点A(1,2),且在两坐标轴上截矩相等的直线方程是___________.
5、直线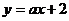 与
与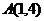 ,
,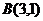 两点确定的线段相交,则
两点确定的线段相交,则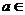 ____________.
____________.
6、函数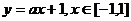 的函数值有正有负,则
的函数值有正有负,则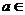 ___________.
___________.
7、如果直线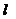 按
按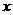 轴负方向平移三个单位,再沿
轴负方向平移三个单位,再沿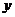 轴正方向平移一个单位后,又回到原来的位置,那么直线
轴正方向平移一个单位后,又回到原来的位置,那么直线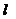 的斜率为_________.
的斜率为_________.
8、一直线经过点P(3,2),且分别满足下列条件,求直线 的方程:(1)倾斜角是直线
的方程:(1)倾斜角是直线
 :
: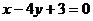 的倾斜角的2倍.(2)某直线被
的倾斜角的2倍.(2)某直线被 、
、 截得的线段的中点恰好在坐标原点,求这条直线的方程.
截得的线段的中点恰好在坐标原点,求这条直线的方程.
9、已知直线 的方程为:
的方程为: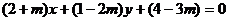 ,
,
(1)求证:不论m为何值,直线必过定点M;
(2)过点M引直线 ,使它与两坐标轴的负半轴所围成的三解形面积最小,求
,使它与两坐标轴的负半轴所围成的三解形面积最小,求 的方程.
的方程.
10、(选做题)
已知长方形四个顶点A(0,0),B(2,0),C(2,1)和D(0,1),一质点从AB的中点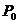 沿与AB夹角为
沿与AB夹角为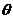 的方向射到BC上的点P
的方向射到BC上的点P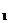 后,依次反射到CD、DA和AB上的点P
后,依次反射到CD、DA和AB上的点P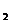 ,
,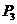 和
和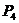 (入射角等于反射角)设
(入射角等于反射角)设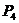 的坐标为(
的坐标为(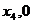 )若1
)若1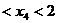 ,则
,则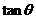 的范围是( )
的范围是( )
A.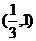 B.
B.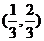 C.
C.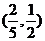 D.(
D.(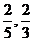 )
)
高三数学教学案 第七章 直线和圆的方程
第二课时 直线的相互关系(一)
考纲摘录
1、掌握两直线平行与垂直的条件;
2、能根据直线方程判定两直线位置关系;
3、熟练求解两直线的夹角,交点及点到直线的距离.
知识概要
 直线平行、垂直的充要条件(斜截式、一般式)
直线平行、垂直的充要条件(斜截式、一般式)
知识点 点到直线的距离公式,平行直线间的距离公式
夹角及到角公式
重点、难点
两直线位置关系的讨论,注意数形结合思想;夹角、到角公式的应用.
基础练习
1、直线 :
: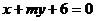 和
和 :
: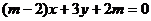 ,当m=_______时,
,当m=_______时, ∥
∥ ;当m=_______时,
;当m=_______时, ⊥
⊥ ;当m=_______时,
;当m=_______时, 与
与 相交;当m=_______时,
相交;当m=_______时, 与
与 重合.
重合.
2、直线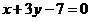 和
和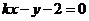 与
与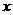 轴、
轴、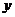 轴正方向所围成的四边形有外接圆,则
轴正方向所围成的四边形有外接圆,则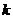 为( )
为( )
A. 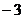 B.6 C.
B.6 C.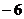 D.3
D.3
3、已知一直线经过点(1,2),并且与点(2,3)和(0,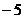 )的距离相等,则直线方程为_________.
)的距离相等,则直线方程为_________.
4、直线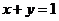 到直线
到直线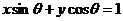 (
(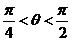 )的角是_________.
)的角是_________.
例题讲解
例1、已知直线 的方程为
的方程为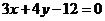 ,按下列条件分别求直线
,按下列条件分别求直线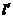 的方程:(1)
的方程:(1)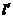 与
与 平行且过点(
平行且过点(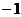 ,3);(2)
,3);(2)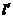 与
与 垂直且
垂直且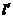 与坐标轴围成的三角形面积为4.
与坐标轴围成的三角形面积为4.
例2、等腰三角形一腰所在直线 的方程是
的方程是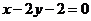 ,底边所在直线
,底边所在直线 的方程是
的方程是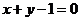 ,点(
,点(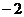 ,0)在另一腰上,求该腰所在直线
,0)在另一腰上,求该腰所在直线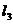 的方程.
的方程.
例3、已知△ABC的顶点A(3,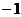 ),AB边上的中线所在直线的方程为
),AB边上的中线所在直线的方程为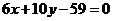 ,∠B的平分线所在直线的方程为
,∠B的平分线所在直线的方程为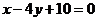 ,求BC边所在直线的方程.
,求BC边所在直线的方程.
例4、直线 过点(1,0),且被两平行直线
过点(1,0),且被两平行直线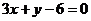 和
和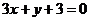 所截得的线段长为9,求直线
所截得的线段长为9,求直线 的方程.
的方程.
课后作业
班级_______学号__________姓名_________
1、若两条直线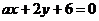 与
与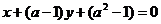 平行且不重合,则
平行且不重合,则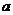 的______.
的______.
2、已知 :
: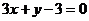 和直线
和直线 :
: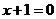 ,则
,则 到
到 的角是 ______________.
的角是 ______________.
3、设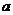 、
、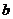 、
、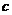 分别是△ABC中∠A、∠B、∠C所对的边长,则直线
分别是△ABC中∠A、∠B、∠C所对的边长,则直线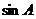 .
.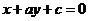 与
与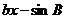 .
.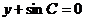 的位置关系是___________.
的位置关系是___________.
4、使三条直线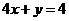 ,
,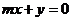 ,
,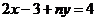 不能围成三角形的实数m的值最多有_______个.
不能围成三角形的实数m的值最多有_______个.
5、若曲线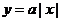 与
与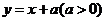 有两个公共点,则
有两个公共点,则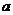 的取值范围是____________.
的取值范围是____________.
6、等腰直角三角形ABC的直角边BC所在直线方程为: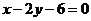 ,顶点A的坐标是(0,6),则斜边AB所在直线的方程是_______________;直角边AC所在直线的方程是_______________.
,顶点A的坐标是(0,6),则斜边AB所在直线的方程是_______________;直角边AC所在直线的方程是_______________.
7、直线 :
: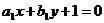 和直线
和直线 :
: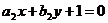 的交点为(2,3),则过两点
的交点为(2,3),则过两点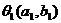 ,
,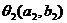 ,的直线方程为________________.
,的直线方程为________________.
8、已知正方形的中心为直线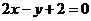 和
和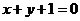 的交点,正方形一边所在直线的方程为
的交点,正方形一边所在直线的方程为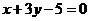 ,求其他三边的方程.
,求其他三边的方程.
9、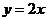 是△ABC中∠C的平分线所在直线的方程,已知
是△ABC中∠C的平分线所在直线的方程,已知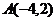 ,
,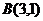 ,求点C的坐标,并判断△ABC的形状.
,求点C的坐标,并判断△ABC的形状.
10、已知直线 :
: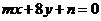 和直线
和直线 :
: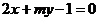 互相平行,求过点(m,n)与
互相平行,求过点(m,n)与 、
、 垂直并且被
垂直并且被 ,
, 截得的弦长为
截得的弦长为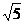 的直线方程.
的直线方程.
高三数学教学案 第七章 直线和圆的方程
第三课时 直线的相互关系(二)
目标要求
掌握利用点点、点线、线线的位置关系处理对称问题;直线相互位置关系的应用.
基础练习
1、点A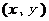 关于直线
关于直线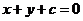 的对称点
的对称点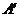 的坐标为_________;关于直线
的坐标为_________;关于直线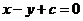 的对称点
的对称点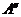 的坐标为_________;曲线
的坐标为_________;曲线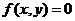 关于直线
关于直线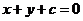 的对称曲线为___________;关于直线
的对称曲线为___________;关于直线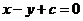 的对称曲线为___________.
的对称曲线为___________.
2、已知 :
: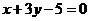 ,过原点关于
,过原点关于 的对称点作
的对称点作 、
、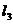 ,使得
,使得 、
、 、
、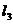 围成等边三角形,则此三角形的面积为___________.
围成等边三角形,则此三角形的面积为___________.
3、已知两点A(8,6)、B(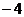 ,0),在直线
,0),在直线 :
: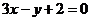 上有一点P,使得
上有一点P,使得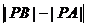 最大,则P点坐标为_________.
最大,则P点坐标为_________.
4、直线 经过点A(3,0),直线
经过点A(3,0),直线 经过点B(0,4),且
经过点B(0,4),且 ∥
∥ ,用
,用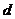 表示
表示 和
和 间的距离,则( )
间的距离,则( )
A. 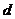 ≥5 B.3≤
≥5 B.3≤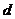 ≤5 C.0≤
≤5 C.0≤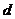 ≤5 D.0<
≤5 D.0<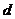 ≤5
≤5
5、已知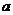 、
、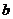 、
、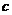 为某一直角三角形的三边长,
为某一直角三角形的三边长,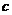 为斜边,若点(
为斜边,若点(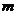 、
、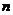 )在直线
)在直线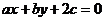 上,则
上,则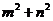 的最小值是____________.
的最小值是____________.
例题讲解
例1、已知直线 和
和 关于直线
关于直线 :
: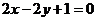 对称,若
对称,若 的方程为
的方程为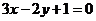 ,求
,求 的方程.
的方程.
例2、已知直线 :
: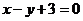 ,一光线从点A(1,2)处射向
,一光线从点A(1,2)处射向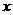 轴上一点B,又从B点反射到
轴上一点B,又从B点反射到 上一点C,最后又从C点反射回A点.
上一点C,最后又从C点反射回A点.
(1)试判断由此得到的△ABC是有限个还是无限个?
(2)依你的判断,认为是无限个时,求出所有这样的△ABC的面积中的最小值,认为是有限个时求出这样的线段BC的方程.
例3、如图所示,一载着重危病人的火车从O地出发,沿射线OA行驶,其中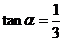 ,在距离O地
,在距离O地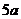 (
(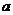 为正数)公里北偏东
为正数)公里北偏东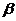 角的N处住有一位医学专家,其中
角的N处住有一位医学专家,其中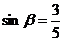 ,现110指挥部紧急征调离O地正东
,现110指挥部紧急征调离O地正东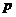 公里的B处的救护车赶往N处载上医学专家全速追赶乘有重危病人的火车,并在C处相遇,经测算当两车行驶的路线与OB围成的三角形OBC面积S最小时,抢求最及时,
公里的B处的救护车赶往N处载上医学专家全速追赶乘有重危病人的火车,并在C处相遇,经测算当两车行驶的路线与OB围成的三角形OBC面积S最小时,抢求最及时,
(1)求S关于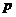 的函数关系;
的函数关系;
 (2)当
(2)当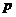 为何值时,抢救最及时.
为何值时,抢救最及时.
北
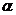
东
课后作业
班级_______学号__________姓名_________
1、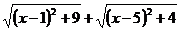 的最小值为______________.
的最小值为______________.
2、入射光沿直线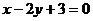 射向直线
射向直线 :
: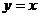 ,被直线
,被直线 反射后的光线所在直线的方程是___________________.
反射后的光线所在直线的方程是___________________.
3、曲线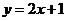 关于点(2,1)对称曲线的方程是_______________.
关于点(2,1)对称曲线的方程是_______________.
4、直线 :
: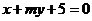 与
与 :
: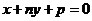 关于
关于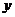 轴对称的充要条件是__________.
轴对称的充要条件是__________.
5、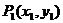 ,
,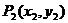 不在直线
不在直线 :
: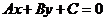 上,且
上,且 交直线
交直线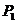
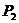 于点
于点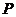 ,则
,则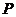 分有向线段
分有向线段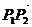 的比为( )
的比为( )
A.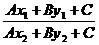 B.
B.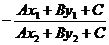
C.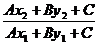 D.
D.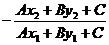
6、在平面直角坐标系中A(0,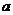 )、B(0,
)、B(0,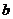 )且
)且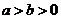 ,在
,在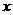 轴的正半轴上求点C,使∠ACB最大,则C点坐标________________.
轴的正半轴上求点C,使∠ACB最大,则C点坐标________________.
7、已知点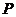 到两个定点
到两个定点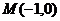 、
、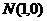 距离的比为
距离的比为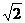 ,点
,点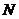 到直线
到直线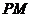 的距离为1.求直线
的距离为1.求直线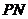 的方程.
的方程.
8、已知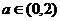 ,直线
,直线 :
: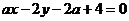 和直线
和直线 :
: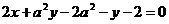 与坐标轴围成一个四边形,要使此四边形的面积最小,求
与坐标轴围成一个四边形,要使此四边形的面积最小,求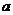 的值.
的值.
9、已知数列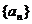 是公差
是公差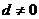 的等差数列,其前
的等差数列,其前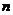 项和为
项和为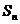
(1)求证:点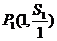 ,
,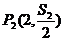 ……
……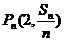 在同一条直线
在同一条直线 上.
上.
(2)若过点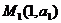 ,
,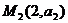 的直线为
的直线为 ,
, 、
、 的夹角为
的夹角为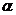 ,求证:
,求证: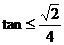 .
.
高三数学教学案 第七章 直线和圆的方程
第四课时 线性规划(一)
考纲摘录
1、了解用二元一次不等式(组)表示平面区域;
2、了解线性规划的意义,并会简单应用,提高解决实际问题的能力.
知识概要
1、二元一次不等式表示平面区域;
2、线性规划(线性约束条件、可行域、目标函数、最优解)
重点、难点
掌握用线性规划的方法解决一些简单实际问题的步骤:
(1)列表、转化为线性规划问题;(2)设出相关变量建立线性约束条件、目标函数;
(3)画出可行域; (4)找出最优解; (5)回答实际问题
基础练习
1、点(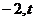 )在直线
)在直线 的上方,则实数
的上方,则实数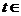 ___________.
___________.
2、可以表示图中阴影部分平面区域的二元一次不等式组是_________________.
3、已知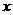 、
、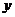 满足
满足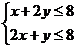 ,目标函数
,目标函数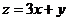 ,当
,当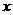 =_________,y=________时,
=_________,y=________时,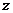 最大值为_________,若又
最大值为_________,若又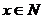 且
且 ,则
,则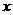 =_________,y=__________时,
=_________,y=__________时,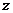 最大值为________.
最大值为________.
4、已知集合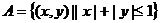 ,集合
,集合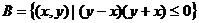 ,
,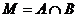 ,则
,则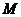 的面积是_________.
的面积是_________.
例题讲解
例1、某工厂制造甲、乙两种产品,已知制造甲产品1kg要用煤9吨,用电力4kw,劳力(按工作日计算)3个;制造乙产品1kg要用煤4吨,电力5kw,劳力10个,又知制成甲产品1kg可获利7万元,制成乙产品1kg可获利12万元,现在工厂只有煤360吨,电力200kw,劳力300个,在这种条件下应生产甲、乙两种产品各多少千克,才能获得最大经济效益?
例2、某人承揽一项业务,需做文字标牌4个,绘画标牌6个,现有两种规格原料,甲种规格每张3㎡,可做文字标牌1个,绘画标牌2个;乙种规格每张2㎡,可做文字标牌2个,绘画标牌1个,求两种规格的原料各用多少张,才能使总的用料面积最小?
例3、某工厂加工零件,要在长度为400cm的圆钢上截取长度为61cm和51cm的甲、乙两种规格的圆钢,怎样截取才能使余料为最少?
课后作业
班级_______学号__________姓名_________
1、点(3,1)和(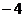 ,6)在直线
,6)在直线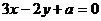 的两侧,则
的两侧,则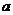 的取值范围是__________.
的取值范围是__________.
2、函数 ,若
,若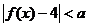 成立的充分条件是
成立的充分条件是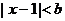 (
(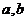 ≥0)画出满足关系的点
≥0)画出满足关系的点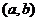 在直角坐标系中表示的区域.
在直角坐标系中表示的区域.
3、三个点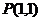 、
、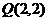 、
、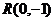 中,落在由方程
中,落在由方程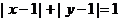 确定的曲线所围成区域中的个数有____________.
确定的曲线所围成区域中的个数有____________.
4、画出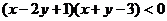 表示的平面区域.
表示的平面区域.
5、实系数方程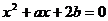 的一个根大于0且小于1,另一个根大于1且小于2,则
的一个根大于0且小于1,另一个根大于1且小于2,则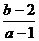 的取值范围是___________.
的取值范围是___________.
6、已知函数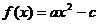 满足
满足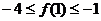 ,
,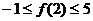 ,求
,求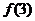 的取值范围.
的取值范围.
7、已知甲、乙两煤矿的日产量分别是200吨和100吨,两矿生产的煤需经 、
、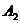 ,车站运往外地,若
,车站运往外地,若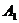 、
、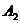 两车站分别最多只能接受160吨.已知甲、乙两矿运往
两车站分别最多只能接受160吨.已知甲、乙两矿运往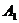 、
、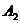 车站的运输价格如表所示,问如何安排运输方案,可使运输费用最低.
车站的运输价格如表所示,问如何安排运输方案,可使运输费用最低.
 车 站
车 站价格(元/吨) 煤 矿 |
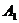 |
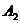 |
|
甲 |
20 |
18 |
|
乙 |
15 |
10 |
8、某工厂的一个车间生产某种产品,其成本为每千克27元,售价为每千克50元.在生产产品的同时,每千克新产品产生出0.3m3的污水,污水有两种排放方式:其一是输送到污水处理厂;其二是直接排入河流.若污水处理厂每小时最大处理能力是0.9m3,处理成本为5元/m3,而且只能净化污水的85%,未净化的污水仍排入河流,环保部门对排入河流的污水收费标准是17.6元/m3,根据环保要求该车间每小时最多允许排入河流中的污水是0.225m3.试问:该车间应选择怎样的生产与排污方案,使其净收益最大.
高三数学教学案 第七章 直线和圆的方程
第五课时 线性规划(二)
目标要求
线性规划的灵活运用.
基础练习
1、给出平面区域如图,如果目标函数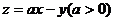 取得最大值的最优解有无穷多个,那么实数
取得最大值的最优解有无穷多个,那么实数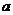 的值是________.
的值是________.
2、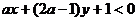 表直线
表直线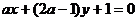 的下方,则
的下方,则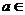 ___________.
___________.
3、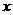 、
、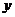 满足
满足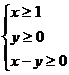 ,则
,则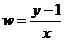 的取值范围是____________.
的取值范围是____________.
4、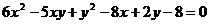 的图象与
的图象与 轴围成的图形的面积是_________.
轴围成的图形的面积是_________.
例题讲解
例1、已知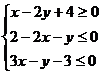 ,试求
,试求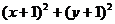 的最大、最小值.
的最大、最小值.
例2、设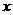 、
、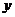 满足
满足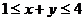 和
和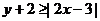 .
.
(1)求点(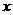 ,
,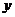 )所表示的平面区域;
)所表示的平面区域;
(2)设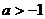 ,在(1)所确定的区域里,求函数
,在(1)所确定的区域里,求函数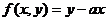 的最大值和最小值.
的最大值和最小值.
例3、长江三峡电厂4台机组发电,每台机组日最大发电量为0.168亿度,每度电输送成本为0.32元,与此同时长江葛州坝电厂有8台机组发电,每台机组日最大发电量为0.12亿度,每度电输送成本为0.35元,由于高温和工业生产,江浙地区用电量增大,日增需求量至少为1.35亿度.
(1)设电力调度总指挥安排三峡电厂有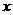 台机组发电,葛州坝电厂有
台机组发电,葛州坝电厂有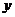 台机组发电,输送江浙地区以填补电力缺口,长江电力公司输送成本为
台机组发电,输送江浙地区以填补电力缺口,长江电力公司输送成本为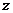 亿元,写出
亿元,写出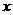 、
、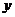 应满足的条件及
应满足的条件及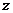 与
与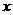 、
、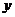 间的函数关系式;
间的函数关系式;
(2)假设你是长江电力公司总经理,为使公司电力输送成本最小,每天如何安排两大电厂的机组数,才可以满足江浙地区用电日增需求量.
课后作业
班级_______学号__________姓名_________
1、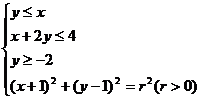 ,则
,则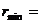 ___________.
___________.
2、实数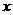 、
、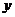 满足条件
满足条件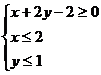 ,则
,则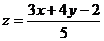 的最大值为_________.
的最大值为_________.
3、设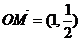 ,
,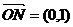 ,则满足条件0≤
,则满足条件0≤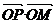 ≤1,0≤
≤1,0≤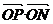 ≤1的动点
≤1的动点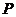 的变动范围是(画图).
的变动范围是(画图).
4、在平面直角坐标系中,横纵坐标都是整数的点称为整点,到点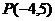 的距离大于2且小于3的整点共___________个;将这些点按到原点的距离从小到大排列,分别记为点
的距离大于2且小于3的整点共___________个;将这些点按到原点的距离从小到大排列,分别记为点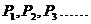 ,则点
,则点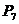 的坐标为___________.
的坐标为___________.
5、4枝郁金香与5枝丁香价格和小于22元,而6枝郁金香与3枝丁香价格之和大于24元,则2枝郁金香与3枝丁香的价格比较结果( )
A.2枝郁金香贵 B.3枝丁香贵 C.相同 D.不定
6、设实数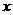 、
、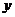 满足
满足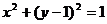 ,当
,当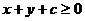 时,
时,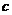 的取值范围是__________.
的取值范围是__________.
7、方程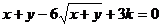 仅表示一条直线,则
仅表示一条直线,则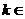 ______________.
______________.
8、已知点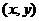 是区域
是区域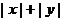 ≤1内的动点,求
≤1内的动点,求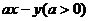 的最大值和最小值.
的最大值和最小值.
9、设直线 过点(0,2),其方向向量为
过点(0,2),其方向向量为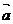 ,向量
,向量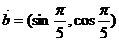 ,向量
,向量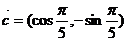 且
且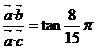 ,求直线
,求直线 的方程.
的方程.