
1、曲线的方程与方程的曲线;
2、求曲线方程的一般步骤;
3、求曲线(轨迹)方程的基本方法.
基础练习
1、已知坐标满足方程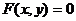 的点都在曲线C上,那么( )
的点都在曲线C上,那么( )
A.曲线C上的点的坐标都适合方程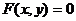
B.坐标不适合方程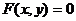 的点都不在曲线C上
的点都不在曲线C上
C.不在曲线C上的点的坐标必不适合方程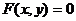
D.不在曲线C上的点的坐标有些合适方程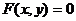 ,有些不适合方程
,有些不适合方程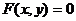
2、下列命题中:
(1)设 ,
,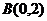 ,则线段的方程为
,则线段的方程为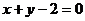 .
.
(2)到原点的距离等于5的动点的轨迹方程是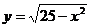 .
.
(3)到两坐标轴距离相等的轨迹方程是
其中正确的命题有( )
A.0个 B.1个 C.2个 D.3个
3、下列四组方程,表示同一曲线的一组是( )
A.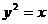 与
与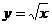 B.
B.
C.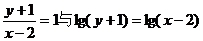 D.
D.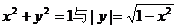
4、若曲线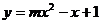 与
与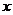 轴有公共点,则
轴有公共点,则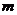 的取值范围是( )
的取值范围是( )
A.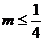 B.
B.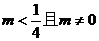 C.
C.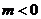 D.
D.
5、曲线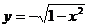 与曲线
与曲线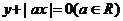 的交点个数一定是( )
的交点个数一定是( )
A.0个 B.2个 C.4个 D.与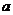 的取值有关
的取值有关
例题讲解
例1、过点 作两条互相垂直的直线
作两条互相垂直的直线 、
、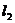 ,
, 交
交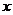 轴于A点,
轴于A点, 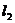 交
交 轴于B点,求线段AB中点M的轨迹方程.
轴于B点,求线段AB中点M的轨迹方程.
例2、已知直角坐标平面上点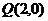 和圆C:
和圆C: ,动点M到圆C的切线长与
,动点M到圆C的切线长与 的比等于常数
的比等于常数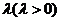 ,求动点M的轨迹方程,并说明它表示什么曲线.
,求动点M的轨迹方程,并说明它表示什么曲线.
例3、过原点O作直线 交抛物线
交抛物线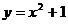 于
于 、
、 两点,求弦
两点,求弦
 中点的轨迹方程.
中点的轨迹方程.
课后作业
班级_______学号__________姓名_________
1、已知△ABC的顶点B(0,0),C(5,0),AB边上的中线长|CD|=3,则顶点A的轨迹方程是______________.
2、已知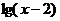 ,
,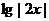 ,
, 成等差数列,则点
成等差数列,则点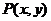 的轨迹方程是___________.
的轨迹方程是___________.
3、若曲线 通过点
通过点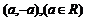 ,则
,则 的取值范围是____________.
的取值范围是____________.
4、直线 与抛物线
与抛物线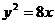 只有一个公共点,则
只有一个公共点,则 的值为( )
的值为( )
A.1 B.1或3 C.0 D.1若0
5、若△ABC的两个顶点B、C的坐标分别是(-1,0)和(2,0),而顶点A在直线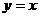 上移动,则△ABC的重心G的轨迹方程是( )
上移动,则△ABC的重心G的轨迹方程是( )
A. B.
B.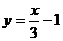 C.
C. D.
D.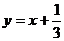
6、作出方程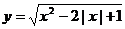 的曲线.
的曲线.
7、已知直线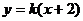 与曲线
与曲线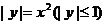 .
.
(1)若 ,求出直线与曲线的交点.
,求出直线与曲线的交点.
(2)若 ,试确定直线与曲线的交点个数.
,试确定直线与曲线的交点个数.
8、已知抛物线C: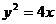 ,O为坐标原点,动直线
,O为坐标原点,动直线 :
: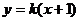 与抛物线C交于A、B两点.
与抛物线C交于A、B两点.
(1)求证 为定值.
为定值.
(2)求满足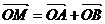 的点M的轨迹方程.
的点M的轨迹方程.
9、(选做题)
已知两定点M(-2, 0),N(2,0),动点P在 轴上的射影是H,如果
轴上的射影是H,如果 ,
,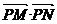 分别是公比为2的等比数列的第三、第四项.
分别是公比为2的等比数列的第三、第四项.
(1)求动点P的轨迹方程C.
(2)已知过点N的直线 交曲线C于
交曲线C于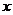 轴下方有两个不同的点A、B,设R为AB的中点,若过点R与定点Q(0,-2)的直线交
轴下方有两个不同的点A、B,设R为AB的中点,若过点R与定点Q(0,-2)的直线交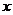 轴于点D
轴于点D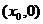 ,求
,求 的取值范围.
的取值范围.
高三数学教学案 第七章 直线和圆的方程
第七课时 圆的方程(一)
考纲摘录
掌握圆的标准方程及一般方程.
知识概要
1、圆的标准方程;
2、圆的一般方程.
基础练习
1、圆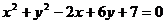 的标准方程为_____________________.
的标准方程为_____________________.
若O (0,0),A(6,-8),则以OA为直径的圆的方程为___________________.
2、在圆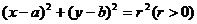 中,
中,
满足____________________________条件时,圆过原点.
满足____________________________条件时,圆心在 轴.
轴.
满足____________________________条件时,圆与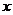 轴相切.
轴相切.
满足____________________________条件时,圆与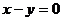 相切.
相切.
满足____________________________条件时,圆与两坐标轴均相切.
3、若方程 表示图,则
表示图,则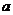 的值为( )
的值为( )
A. B.
B.
C.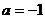 D.
D.
4、方程 和
和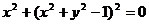 ,它的表示的图形是( )
,它的表示的图形是( )
A.都是两个点 B.一条直线和一个圆
C.前者表示两个点,后者是一条直线和一个圆
D.前者是一条直线和一个圆,后者是两个点
例题讲解
例1、根据下列条件求圆的方程
(1)经过坐标原点和点P(1,1),并且圆心在直线上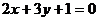 上;
上;
(2)经过P(-2,4),Q(3,-1)两点,并且在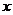 轴上截得的弦长等于6;
轴上截得的弦长等于6;
(3)求与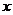 轴相切,圆心在直线
轴相切,圆心在直线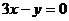 上,且被直线
上,且被直线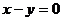 截下的弦长为
截下的弦长为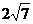 的圆的方程.
的圆的方程.
例2、在以O为原点的直角坐标系中,点A(4,-3)为△OAB的直角顶点,已知|AB|=2|OA|,且点B的纵坐标大于0.
(1)求向量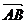 的坐标;
的坐标;
(2)求圆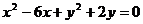 关于直线OB对称的圆的方程.
关于直线OB对称的圆的方程.
例3、如图是某圆拱桥的一孔圆拱的示意图,该圆拱跨度AB=20米,拱高OP=4米,在建造时,每隔4米需用一支柱支撑,求支柱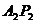 的长度(精确到0.01米).
的长度(精确到0.01米).

课后作业
班级_______学号__________姓名_________
1、方程 表示圆的充要条件是( )
表示圆的充要条件是( )
A.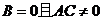 B.
B.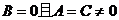
C.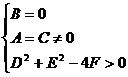 D.
D.
2、圆C的原点为圆心,且在直线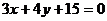 上截得弦长为8,则圆C的方程是__________________.
上截得弦长为8,则圆C的方程是__________________.
3、已知A(0,1),B(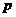 ,
,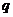 )
) ,则以AB为直径的圆与
,则以AB为直径的圆与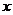 轴的交点的横坐标一定是二次方程________________________.
轴的交点的横坐标一定是二次方程________________________.
4、方程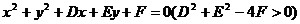 表示的曲线关于
表示的曲线关于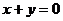 的成轴对称图形,则( )
的成轴对称图形,则( )
A.D+E=0 B.D+F=0 C.E+F=0 D.D+E+F=0
5、直线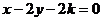 与
与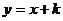 的交点在曲线
的交点在曲线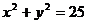 上,则
上,则 的值是( )
的值是( )
A.1或5 B.-1或-5 C.±1 D.±5
6、方程 所表示的封闭曲线所围成的图形面积为___________________.
所表示的封闭曲线所围成的图形面积为___________________.
7、已知圆的方程为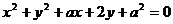 ,若过定点
,若过定点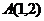 作圆的切线有两条,求
作圆的切线有两条,求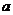 的取值范围.
的取值范围.
8、(1)求圆心在原点,且圆周被直线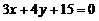 分成1:2两部分的圆的方程.
分成1:2两部分的圆的方程.
(2)求△ABC的外接圆方程,其中A(-2,-1),B(-1,-1),C(- ,-
,-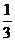 ).
).
(3)求过点A(4,-1) ,且与已知圆 切于点B(1,2)的圆方程.
切于点B(1,2)的圆方程.
高三数学教学案 第七章 直线和圆的方程
第八课时 圆的方程(二)
考纲摘录
了解参数方程的概念,理解圆的参数方程及参数 的意义,能用圆的几何性质与圆的知识解题.
的意义,能用圆的几何性质与圆的知识解题.
知识概要
1、圆的参数方程;
2、圆的相关知识.
基础练习
1、已知圆O的参数方程是 圆O上点P的坐标是
圆O上点P的坐标是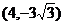 ,则P点对应的参数
,则P点对应的参数 等于( )
等于( )
A. B.
B. C.
C. D.
D.
2、点P(3,0)是圆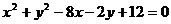 内一点,过点P的弦中最短的弦所在直线方程是( )
内一点,过点P的弦中最短的弦所在直线方程是( )
A. B.
B.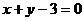 C.
C.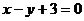 D.
D.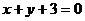
3、两圆相交于两点(1,3)和(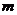 ,
,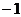 )两圆圆心都在
)两圆圆心都在 直线上,则
直线上,则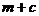 的值为( )
的值为( )
A.-1 B.2 C.3 D.0
4、由动点P向圆 引两条切线PA、PB,切点分别为A、B,
引两条切线PA、PB,切点分别为A、B, 则动点P的轨迹方程为__________________.
则动点P的轨迹方程为__________________.
例题讲解
例1、已知方程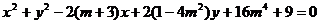 表示一个圆,
表示一个圆,
(1)求实数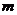 的取值范围;
的取值范围;
(2)求该圆半径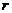 的取值范围;
的取值范围;
(3)求圆心的轨迹方程.
例2、(1)求圆心在直线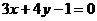 上且过两圆
上且过两圆 与
与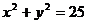 的交点的圆的方程.
的交点的圆的方程.
(2)求过直线 和圆
和圆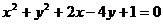 交点且面积最小的圆的方程
交点且面积最小的圆的方程
例3、在△ABC中,已知 ,C=10,P是内切圆上一点,求
,C=10,P是内切圆上一点,求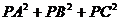 的最大值与最小值.
的最大值与最小值.
课后作业
班级_______学号__________姓名_________
1、点P从(1,0)出发,沿半径圆 逆时针方向运动
逆时针方向运动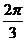 孤长到达Q点,则Q的坐标为______________.
孤长到达Q点,则Q的坐标为______________.
2、在圆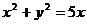 内,过点
内,过点 有
有 条弦的长度成等差数列,最短弦长为数列的首项
条弦的长度成等差数列,最短弦长为数列的首项 ,最长弦长为
,最长弦长为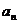 ,若公差
,若公差 ,那么
,那么 的取值集合为( )
的取值集合为( )
A.{4,5,6} B.{6,7,8,9} C.{3,4,5} D.{3,4,5,6}
3、两圆 ,
,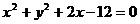 相交于A、B两点,则直线AB的方程是________________________.
相交于A、B两点,则直线AB的方程是________________________.
4、直线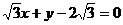 截圆
截圆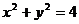 得的劣弧所对的圆心角为( )
得的劣弧所对的圆心角为( )
A. B.
B.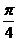 C.
C. D.
D.
5、若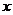 、
、 满足
满足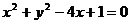 ,则
,则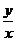 的最大值为___________,
的最大值为___________,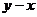 的最小值为__________.
的最小值为__________.
6、已知两点A(0,1),B(2,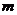 ),如果经过A与B且与
),如果经过A与B且与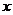 轴相切的圆有且只有一个,求
轴相切的圆有且只有一个,求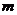 的值及圆的方程.
的值及圆的方程.
7、已知直线 :
: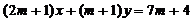 ,圆C:
,圆C: .
.
(1)求证:直线 与圆C总相交.
与圆C总相交.
(2)求出相交的弦长的最小值及对应的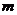 值.
值.
8、MN是圆 的弦,且MN⊥
的弦,且MN⊥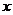 轴(如图)设圆O与
轴(如图)设圆O与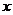 轴交于A、B,求直线AM、BN的交点P的轨迹方程.
轴交于A、B,求直线AM、BN的交点P的轨迹方程.
高三数学教学案 第七章 直线和圆的方程
第九课时 直线与圆的位置关系(一)
考纲摘录
掌握直线与圆、圆与圆的位置关系、会求圆的切线方程及弦长等有关直线与圆的内容.
知识概要
1、直线与圆的位置关系(相离、相切、相交),判断方法(代数法、几何法);
2、圆与圆的位置关系(相离、外切、相交、内切、内含);
3、圆的切线切线方程.
基础练习
1、已知圆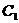 :
: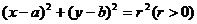 ,直线
,直线 :
: ,
,
当__________________________时, 与圆
与圆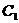 相交.
相交.
若另有一圆 :
: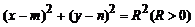 .
.
当__________________________时,两圆外切.
当__________________________时,两圆内切.
当__________________________时,两圆相交.
2、若圆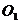 :
: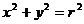 ,圆
,圆 :
: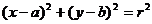 ,则以
,则以 为切点的圆
为切点的圆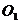 的切线方程为_____________________________________________
的切线方程为_____________________________________________
圆 的切线方程为_____________________________________________
的切线方程为_____________________________________________
3、直线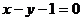 被圆
被圆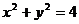 所截得的弦长为_______________
所截得的弦长为_______________
4、过点M(2,4)向圆 引切线,则切线方程是_________________.
引切线,则切线方程是_________________.
5、两个圆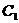 :
: 与圆
与圆 :
: 的公切线有且仅有( )
的公切线有且仅有( )
A.1条 B.2条 C.3条 D.4条
例题讲解
例1、过点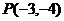 作直线
作直线 ,当斜率为何值时,
,当斜率为何值时, 与圆
与圆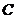 :
: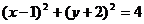 有公共点.
有公共点.
例2、设圆上的点A(2,3)关于直线 的对称点仍在圆上,且与直线
的对称点仍在圆上,且与直线 相交的弦长为
相交的弦长为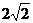 ,求圆的方程.
,求圆的方程.
例3、已知圆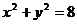 ,定点P(4,0),问过P点的直线的倾斜角在什么范围内取值时,该直线与已知圆(1)相切;(2)相交;(3)相离.
,定点P(4,0),问过P点的直线的倾斜角在什么范围内取值时,该直线与已知圆(1)相切;(2)相交;(3)相离.
例4、过点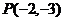 作圆
作圆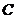 :
: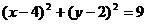 的两条切线、切点分别为A、B.
的两条切线、切点分别为A、B.
求(1)经过圆心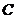 、切点A、B这三点圆的方程;
、切点A、B这三点圆的方程;
(2)直线AB的方程;
(3)线段AB的长.
课后作业
班级_______学号__________姓名_________
1、若半径为1的动圆与圆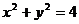 相切,则动圆圆心的轨迹的方程是( )
相切,则动圆圆心的轨迹的方程是( )
A.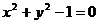 B.
B.
C. D.
D.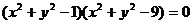
2、设M是圆 上的点,则M点到直线
上的点,则M点到直线 的最短矩离是( )
的最短矩离是( )
A.9 B.8 C.5 D.2
3、两圆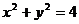 与
与 交于M、N两点,则公共弦方程为________________________,公共弦长|MN|=_________.
交于M、N两点,则公共弦方程为________________________,公共弦长|MN|=_________.
4、若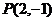 为圆
为圆 的弦AB的中点,则直线AB的方程是________________________.
的弦AB的中点,则直线AB的方程是________________________.
5、圆 上到直线
上到直线 的距离为
的距离为 的点共有( )
的点共有( )
A.1个 B.2个 C.3个 D.4个
6、已知圆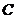 :
: ,
,
(1)求过点A(3,5)的圆的切线方程;
(2)在两坐标轴上截距相等的圆的切线方程.
7、自点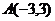 发出的光线
发出的光线 射到
射到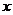 轴上,被
轴上,被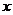 轴反射,其反射光线
轴反射,其反射光线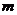 所在的直线与圆
所在的直线与圆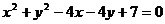 相切,求光线
相切,求光线 与
与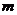 所在直线的方程.
所在直线的方程.
8、已知圆 与直线
与直线 相交于两点
相交于两点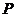 、
、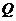 ,
,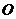 为坐标原点,求
为坐标原点,求 的值.
的值.
高三数学教学案 第七章 直线和圆的方程
第十课时 直线与圆的位置关系(二)
知识目标
提高解决与圆有关知识的综合能力.
基础练习
1、已知点 和圆C
和圆C 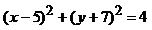 ,一束光线以点
,一束光线以点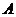 经
经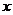 轴反射到圆周C的最短距离是( )
轴反射到圆周C的最短距离是( )
A. B.
B. C.8 D.10
C.8 D.10
2、已知P是直线 上的动点,PA、PB是圆
上的动点,PA、PB是圆 的两条切线,A、B是切点,C是圆心,那么四边形PACB面积的最小值是_______________.
的两条切线,A、B是切点,C是圆心,那么四边形PACB面积的最小值是_______________.
3、曲线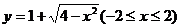 与直线
与直线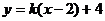 有两个不同的交点时,实数
有两个不同的交点时,实数 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C. D.
D.
4、从原点向圆 作两条切线,则该圆夹在两条切线间的劣弧长为( )
作两条切线,则该圆夹在两条切线间的劣弧长为( )
A. B.2
B.2 C.4
C.4 D.6
D.6
例题讲解
例1、已知圆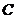 :
: 和直线
和直线 :
: ,
,
(1)求证,对 ,直线
,直线 与圆
与圆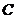 总有两个交点;
总有两个交点;
(2)若定点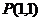 分弦AB为
分弦AB为 ,求此直线
,求此直线 的方程.
的方程.
例2、过点M(3,0)作直线 与圆
与圆 交于A、B两点,求直线
交于A、B两点,求直线 的倾斜角,使△AOB的面积最大,并求出这个最大值.
的倾斜角,使△AOB的面积最大,并求出这个最大值.
例3、从圆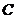 :
: 外一点P(
外一点P(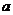 ,
, )向圆引切线PT,T为切点,且|PT|=|PO|(O为原点),求|PT|的最小值及此时P的坐标.
)向圆引切线PT,T为切点,且|PT|=|PO|(O为原点),求|PT|的最小值及此时P的坐标.
|

 方向300km的海面P处,并以20km/h的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当
半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?
方向300km的海面P处,并以20km/h的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当
半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?


|

|
 .
.
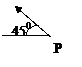
课后作业
班级_______学号__________姓名_________
1、过原点的直线与圆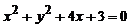 相切,若切点在第三象限,则该直线的方程是( )
相切,若切点在第三象限,则该直线的方程是( )
A.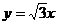 B.
B.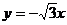 C.
C.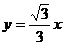 D.
D.
2、如果直线 将圆
将圆 平分,且不通过第四象限那么直线
平分,且不通过第四象限那么直线 的斜率的取值范围是( )
的斜率的取值范围是( )
A.[0,2] B.[0,1] C.[0,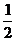 ] D.
] D.
3、曲线C: (
( 为参数)的普通方程是_______________,如果曲线C与
为参数)的普通方程是_______________,如果曲线C与 直线有公共点,那么实数
直线有公共点,那么实数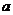 的取值范围是______________________.
的取值范围是______________________.
4、集合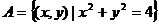 ,
,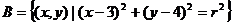 ,其中
,其中 ,若A∩B中有且只有一个元素,则
,若A∩B中有且只有一个元素,则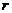 的值是___________.
的值是___________.
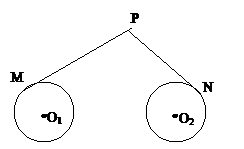
5、如图,圆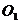 和圆
和圆 的半径都等于1,
的半径都等于1,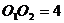 过动点P分别作圆
过动点P分别作圆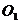 、圆
、圆 的切线PM、PN(M、N为切点),使得PM=
的切线PM、PN(M、N为切点),使得PM= PN,试建立平面直角坐标系,求动点P的轨迹方程.
PN,试建立平面直角坐标系,求动点P的轨迹方程.
6、设圆满足:(1)截 轴所得的弦长为2;
轴所得的弦长为2;
(2)被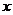 轴分成两段圆弧,其弧长的比为3:1
轴分成两段圆弧,其弧长的比为3:1
在满足条件(1)(2)的所有圆中,求圆心到直线 :
: 的距离最小的圆的方程.
的距离最小的圆的方程.
7、已知动圆过定点P(1,0),且与定直线 :
: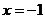 相切,点C在
相切,点C在 上,
上,
(1)求动圆圆心的轨迹M的方程;
(2)设过点P,且斜率为 的直线与曲线M相交于A、B两点
的直线与曲线M相交于A、B两点
①问:△ABC能否为正三角形?若能,求出点C的坐标3,若不能,请说明理由.
②当△ABC为钝角三角形时,求这种点C的纵坐标的取值范围.