
1、在已知二面角大小的条件下,求其几何量的问题;
2、折叠问题必需掌握原始平面图形的主要元素和折叠后所形成的立体图形的主要元素之间的对应关系,其中有些元素的量在变化,有些元素的量是不变的.
基础练习
1、平面 内有一以AB为直径的圆,PA⊥
内有一以AB为直径的圆,PA⊥ ,点C在圆周上移动(不与A、B重合)点D、E分别是A在PC、PB上的射影,下面结论
,点C在圆周上移动(不与A、B重合)点D、E分别是A在PC、PB上的射影,下面结论
(1)∠AED是二面角A-PB-C的平面角;
(2)∠ACD是二面角P-BC-A的平面角;
(3)∠EDA是二面角A-PC-B的平面角;
(4)∠DAE是二面角B-PA-C的平面角;
(5)∠PAC是二面角P-AB-C的平面角;
其中正确结论的序号是___________.
2、在正△ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后BC= AB,这时二面角B-AD-C的大小为( )
AB,这时二面角B-AD-C的大小为( )
A.60° B. 90° C.45° D.120°
3、在60°的二面角的一个面所在的平面内有一条直线与二面角的棱成60°的角,则此直线与二面角的另一个面所在的平面所成的角的正弦值是( )
A.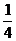 B.
B. C.
C.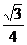 D.1
D.1
4、有一山坡,它的倾斜度(坡面与水平面所成的二面角的度数)为30°,有一名学生骑车沿山坡一条与坡脚水平线成60°的直路向上走了100m,那么他比水平面升高了( )
A.20m B.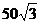 m C.
m C. m D.25m
m D.25m
5、菱形ABCD的对角线AC=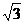 ,沿BD把面ABD折起与面BCD成120°的二面角后,点A到面BCD的距离为___________.
,沿BD把面ABD折起与面BCD成120°的二面角后,点A到面BCD的距离为___________.
例题讲解
例1、在矩形ABCD中,AB=6,BC=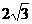 ,沿对角线BD将△ABD向上折起,使点A移至点P,且P点在平面BCD的射影O在DC上.
,沿对角线BD将△ABD向上折起,使点A移至点P,且P点在平面BCD的射影O在DC上.
(1)求证:PD⊥PC;
(2)求二面角P-BD-C的平面角的余弦值.
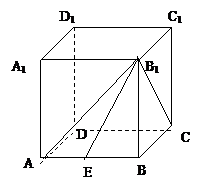 例2、在正方体ABCD-A1B1C1D1中,E在AB上,且AB=a,当二面角A-B1E-C为
例2、在正方体ABCD-A1B1C1D1中,E在AB上,且AB=a,当二面角A-B1E-C为
120°,求BE的长.
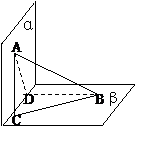 例3、已知直二面角
例3、已知直二面角 -
-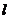 -
- ,A∈
,A∈ ,B∈
,B∈ ,线段AB=2a,AB与
,线段AB=2a,AB与 成45°角,与
成45°角,与 成30°角,过A、B两点分别作棱
成30°角,过A、B两点分别作棱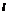 的垂线AC、BD,求面ABD与面ABC所成的二面角的大小.
的垂线AC、BD,求面ABD与面ABC所成的二面角的大小.
课后作业
班级_______学号__________姓名_________
1、把边长为 的正三角形ABC沿高AD折成60°的二面角,则A到BC的距离是( )
的正三角形ABC沿高AD折成60°的二面角,则A到BC的距离是( )
A.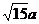 B.
B.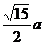 C.
C.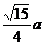 D.
D.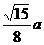
2、二面角 -AB-
-AB- 的平面角是锐角,C是平面
的平面角是锐角,C是平面 内的点(不在棱AB上)D是C在平面
内的点(不在棱AB上)D是C在平面 上的射影,E是棱AB上满足∠CEB为锐角的任意一点,则( )
上的射影,E是棱AB上满足∠CEB为锐角的任意一点,则( )
A.∠CEB>∠DEB B.∠CEB=∠DEB
C.∠CEB<∠DEB D.∠CEB与∠DEB的大小不能确定
3、在直角坐标系中,设A(3,2),B(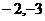 )沿
)沿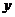 轴把直角坐标系平面折成120°的二面角后AB的长是________.
轴把直角坐标系平面折成120°的二面角后AB的长是________.
4、二面角 -
-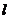 -
- 的度数为120°,A、B∈
的度数为120°,A、B∈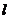 ,AC
,AC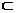
 ,BD
,BD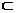
 ,AC⊥
,AC⊥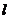 ,BD⊥
,BD⊥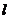 ,若AB=AC=BD=1,则CD等于__________.
,若AB=AC=BD=1,则CD等于__________.
5、已知正方形ABCD,AC、BD相交于O点,若将正方形ABCD沿对角线BD折成60°的二面角,并给出四个结论
①AC⊥BD ②AD⊥CO ③AOC为正三角形 ④cos∠ADC= ,
,
则其中正确结论的序号是__________.(注:把你认为正确的序号都填上)
6、平面四边形ABCD中,AB=BC=CD= ,∠B=90°,∠DCB=135°沿对角线AC将四边形折成直二面角.
,∠B=90°,∠DCB=135°沿对角线AC将四边形折成直二面角.
(1)证明:AB⊥面BCD;
(2)求面ABD与面ACD所成的角.
7、如图,在斜三棱柱ABC-A1B1C1中,已知侧面BCC1B1为矩形,侧棱与底面成30°的角,底面△ABC的面积是截面A1BC的面积的2倍,求二面角A-BC-A1的大小.

8、(选做题)如图,在Rt△ABC中,AB=BC,E、F分别是AC和AB的中点,以EF为棱把它折成大小为 的二面角A-EF-B,设∠AEC=
的二面角A-EF-B,设∠AEC= ,求证:
,求证: .
.

高三数学教学案 第九章 立体几何
第十三课时 空间角的计算
考纲摘录
理解线线角、线面角、面面角的定义,依定义作出有关角,然后抓住有关的三角形来解决.
基础练习
1、设正方体ABCD-A1B1C1D1中六个面内的对角线共有n条与BD成60°角,则n等于( )
A.0 B.2 C.4 D.8
2、已知直线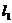 与平面
与平面 成
成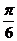 的角,直线
的角,直线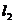 与
与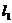 成
成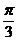 的角,则
的角,则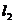 与平面
与平面 所成角的范围是( )
所成角的范围是( )
A.[0,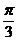 ] B.[
] B.[ ,
,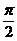 ] C.[
] C.[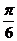 ,
,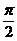 ] D.[0,
] D.[0,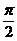 ]
]
3、将∠A为60°的菱形ABCD,沿对角线BD折叠,使A、C的距离等于BD,则二面角A-BD-C的余弦值是___________.
4、二面角 -
-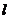 -
- 是直二面角,A
是直二面角,A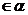 ,B
,B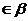 ,A、B
,A、B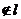 ,设直线AB与
,设直线AB与 、
、 所成的角分别为
所成的角分别为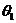 、
、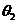 则(
)
则(
)
A.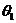 +
+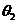 =90° B.
=90° B.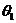 +
+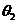 ≥90° C.
≥90° C.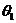 +
+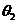 ≤90° D.
≤90° D.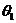 +
+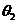 ≠90°
≠90°
5、正方体ABCD-A1B1C1D1中M、N分别为A1D1和DD1的中点,过平行线MN与B1C作截面MB1CN,令二面角M-B1C-C1的大小为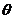 ,则
,则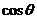 等于( )
等于( )
A.0
B. C.
C.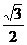 D.
D.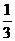
例题讲解
例1、在120°的二面角 -
-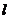 -
- 中,A∈
中,A∈ ,B∈
,B∈ ,已知点A和B到棱
,已知点A和B到棱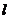 的距离分别为2和4,且AB=10,求.
的距离分别为2和4,且AB=10,求.
(1)直线AB与棱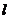 所成的角;
所成的角;
(2)直线AB与平面 所成的角.
所成的角.
例2、设△ABC和△DBC所在的平面互相垂直,且AB=BC=BD,∠ABD=∠DBC=120°
求:(1)直线AD和平面BCD所成的角的大小;
(2)异面直线AD与BC所成角的大小;
(3)二面角A-BD-C的大小.
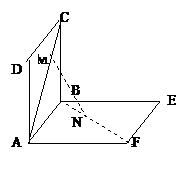
例3、如图所示,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN= (0<
(0< <
<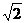 )
)
(1)求MN的长;
(2)当 为何值时,MN的长最小;
为何值时,MN的长最小;
(3)若MN长最小时,求面MNA与面NMB所成的二面角 的大小.
的大小.
、
课后作业
班级_______学号__________姓名_________
1、二面角M-AB-N为 ,AC
,AC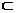 平面M,∠CAB=
平面M,∠CAB= ,AC与平面N成
,AC与平面N成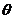 角,则
角,则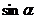 、
、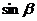 、
、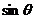 之间的关系式___________.
之间的关系式___________.
2、已知正方形ABCD,沿对角线AC将三角形ADC折起,设AD与平面ABC所成角为 ,当
,当 取最大值时,二面角B-AC-D等于( )
取最大值时,二面角B-AC-D等于( )
A.45° B.90° C. D.
D.
3、二面角M-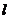 -N大小为
-N大小为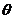 ,Rt△ABC在面M内,斜边AB在
,Rt△ABC在面M内,斜边AB在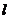 上,直角边AC、BC与平面N所成角分别为
上,直角边AC、BC与平面N所成角分别为 、
、 ,判断
,判断 的关系
的关系
4、正三棱锥的一个侧面的面积与底面积之比为2:3,则这个三棱锥的侧面和底面所成的二面角为_________度.
5、已知∠AOB=90°,过O点引∠AOB所在平面的斜线OC,与OA、OB分别成45°、
60°的角,则以OC为棱的二面角的余弦值为__________.
6、正方体ABCD-A1B1C1D1中,E、F分别为B1C1、C1D1的中点,若截面EFDB与侧面BCC1B1所成锐二面角为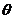 ,则
,则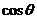 =__________.
=__________.
7、如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=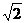 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
(1)求证:AM∥平面BDE;
(2)求二面角A-DF-B的大小;
(3)试在线段AC上确定一点P,使PF与BC、EF所成的角为60°.

8、四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将∠ABD沿对角线BD折起,记折起点A的位置为P,且使平面PBD⊥平面BCD.
(1)求证:平面PBC⊥平面PDC;
(2)求二面角P-BC-D的大小.
高三数学教学案 第九章 立体几何
第十四课时 距离(一)
考纲摘录
1、掌握空间两条直线、直线和平面,两个平面及点到平面距离的概念;
2、对于异面直线的距离,只要求会计算已给出公垂线时的距离.
知识概要
1、空间距离的求法是教材的重要内容也是历年高考考查的重点,其中点与点、点到线、点到面的距离为基础,求其它几种距离一般应化归为求这三种距离;
2、点到面的距离是空间最常见的,也是应用最多的,求解的关键是正确的作出图形,其中确定垂足位置最重要;
3、求距离的一般步骤:(1)找出或作出有关距离;(2)证明它符合定义;(3)归到某三角形中形算.
基础练习
1、将锐角为60°,边长为 的的菱形ABCD沿较短的对角线BD折成60°的二面角,则AC与BD之间的距离为___________.
的的菱形ABCD沿较短的对角线BD折成60°的二面角,则AC与BD之间的距离为___________.
2、直线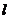 ∥平面
∥平面 ,
,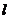 与
与 间的距离为b,则到直线
间的距离为b,则到直线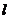 的距离和到平面
的距离和到平面 的距离都等于
的距离都等于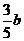 的点的集合是( )
的点的集合是( )
A.一条直线 B.两条平行线 C.一个平面 D.两个平面
3、已知AD是边长为2的正三角形ABC的边BC上的高,沿AD将△ABC折成直二面角B-AD-C后,点B到AC的距离为( )
A.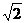 B.
B.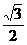 C.
C.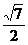 D.1
D.1
4、已知线段AB在平面 外,AB两点到平面
外,AB两点到平面 的距离分别是1和3,则线段AB中点到平面
的距离分别是1和3,则线段AB中点到平面 的距离是___________.
的距离是___________.
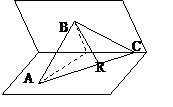
5、A、B是直线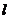 上的两点,AB=4,AC⊥
上的两点,AB=4,AC⊥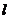 于A,BD⊥
于A,BD⊥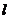 于B,AC=BD=3,又AC与BD成60°的角,则C、D两点间的距离是___________.
于B,AC=BD=3,又AC与BD成60°的角,则C、D两点间的距离是___________.
例题讲解
例1、已知AB是异面直线 、
、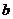 的公垂线段,A∈
的公垂线段,A∈ ,B∈
,B∈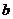 ,AB=2,
,AB=2, 、
、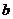 成30°角,在直线
成30°角,在直线 上取一点P,使PA=4,求P点到直线
上取一点P,使PA=4,求P点到直线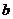 的距离.
的距离.
例2、已知△ABC在平面 内,DA⊥
内,DA⊥ ,EB⊥
,EB⊥ ,DC与
,DC与 成30°角且DC⊥BC,若EB=BC=DC=
成30°角且DC⊥BC,若EB=BC=DC= ,求DE的长.
,求DE的长.
例3、如图,已知二面角 -PQ-
-PQ- 为60°,点A和点B分别在平面
为60°,点A和点B分别在平面 和平面
和平面 上,点C 在棱PQ,∠ACP=∠BCP=30°,CA=CB=
上,点C 在棱PQ,∠ACP=∠BCP=30°,CA=CB=
(1)求证:AB⊥PQ;
(2)求点B到平面 的距离
的距离
(3)设R是线段CA上的一点,直线BR与平面 所成的角为45°,求线段CR的长度.
所成的角为45°,求线段CR的长度.
课后作业
班级_______学号__________姓名_________
1、平面外一条直线上的两个点到这个平面的距离相等,则这条直线与这个平面( )
A.一定平行 B.一定相交 C.平行或相交 D.一定垂直
2、在正方体ABCD-A1B1C1D1中,P是侧面BB1C1C内一动点,若P到直线BC与直线C1D1的距离相等,则动点P的轨迹所在的曲线是( )
A.直线 B.圆 C.双曲线 D.抛物线
3、在矩形ABCD中,AB=3,BC=4,PA⊥平面ABCD,且AP=1,则P点到对角线BD的距离为( )
A.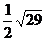 B.
B.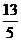 C.
C.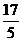 D.
D.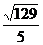
4、在两个互相垂直的平面的交线上有两点A、B,AC和BD分别是这两个平面内垂直于AB的线段,AC=6,AB=8,BD=24,则C、D间距离为__________.
5、△ABC的三个顶点A、B、C到平面 的距离分别为2,3,4,且它们在
的距离分别为2,3,4,且它们在 的同侧,则△ABC的重心到平面
的同侧,则△ABC的重心到平面 的距离为__________.
的距离为__________.
6、已知Rt△ABC的直角顶点C在平面 内,斜边AB∥
内,斜边AB∥ ,AB=
,AB= ,AC、BC分别和平面
,AC、BC分别和平面 成45°和30°角,求AB到平面
成45°和30°角,求AB到平面 的距离.
的距离.
7、已知 -
-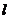 -
- 的大小是60°,AB
的大小是60°,AB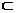
 ,CD
,CD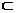
 ,并且AB⊥
,并且AB⊥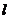 于A,CD⊥
于A,CD⊥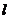 于C,AB=AC=CD=
于C,AB=AC=CD= ,求:
,求:
(1)B、D两点间的距离;
(2)点D到AB的距离.
8、如图,在正三棱柱ABC-A1B1C1中,各棱长都等于 ,D、F分别为AC1和BB1的中点
,D、F分别为AC1和BB1的中点
(1)求证:DF为异面直线AC1和BB1的公垂线段并求其长度;
(2)求点C1到平面AFC的距离.
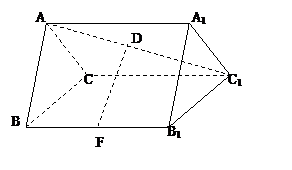
高三数学教学案 第九章 立体几何
第十五课时 距离(二)
考纲摘录
进一步掌握空间两条直线、直线和平面、两个平面及点到平面距离的求法.
知识概要
1、点到平面的距离;
2、各种距离之间的相互转化,等体积法及“平行移动”等思想方法.
基础练习
1、在正方体ABCD-A1B1C1D1中,AB= ,M是AA1的中点,则点A1到平面MBD的距离是( )
,M是AA1的中点,则点A1到平面MBD的距离是( )
A.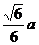 B.
B.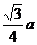
C.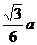 D.
D.
2、四棱锥P-ABCD的底面为正方形PD⊥底面ABCD,PD=AD=1,设点C到平面PAB的距离为d1,点B到平面PAC的距离为d2,BC到平面PAD的距离为d3,则有( )
A.d3<d1<d2 B.d1<d2<d3 C.d1<d3<d2 D.d2<d1<d3
3、若三棱锥P-ABC中过点P的三条侧棱两两垂直,长都是 ,则底面上任一点到三个侧面距离之和为___________.
,则底面上任一点到三个侧面距离之和为___________.
4、 ∩
∩ =MN,A∈
=MN,A∈ ,C∈MN,且∠ACM=45°,
,C∈MN,且∠ACM=45°, -MN-
-MN- 是60°的二面角,AC=1,则点A到平面
是60°的二面角,AC=1,则点A到平面 的距离___________.
的距离___________.
5、直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=AA1= ,则点A到平面A1BC的距离是___________.
,则点A到平面A1BC的距离是___________.
 例题讲解
例题讲解
例1、在棱长为1的正方体ABCD-A1B1C1D1中
(1)求点A到平面BD1的距离;
(2)求点A1到平面AB1D1的距离;
(3)求平面AB1D1与平面BC1D的距离;
(4)求直线AB到平面CDA1B1的距离.
 例2、棱长为4的正方体ABCD-A1B1C1D1中,P、Q分别为棱CD、CD1的中点,求P到平面A1QC1的距离.
例2、棱长为4的正方体ABCD-A1B1C1D1中,P、Q分别为棱CD、CD1的中点,求P到平面A1QC1的距离.
 例3、如图,在矩形ABCD中,AB=
例3、如图,在矩形ABCD中,AB= ,BC=3,沿对角线BD将△BDC折起,使点C移到点E,且点E在平面ABD上的射影H恰在AB上.
,BC=3,沿对角线BD将△BDC折起,使点C移到点E,且点E在平面ABD上的射影H恰在AB上.
(1)求证:BE⊥平面ADE;
(2)求点A到平面BDE的距离.
课后作业
班级_______学号__________姓名_________
1、△ABC中,AB=9,AC=15,∠BAC=120°,△ABC所在平面外一点P到三个顶点A、B、C的距离都是14,那么点P到平面 的距离( )
的距离( )
A.7 B.9 C.11 D.13
2、平面 内有∠XOY=60°,OA是
内有∠XOY=60°,OA是 的斜线且OA=10,∠AOX=∠AOY= 60°,则A到
的斜线且OA=10,∠AOX=∠AOY= 60°,则A到 的距离是__________.
的距离是__________.
3、在四面体P-ABC,PA、PB、PC两两垂直,M是面ABC内一点且点M到三个面PAB、PBC、PCA的距离分别是2、3、6,则点M到顶点P的距离是( )
A.7 B.8 C.9 D.10
4、四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底面边长均为2 ,且∠A1AD=∠A1AB=60°,则侧棱AA1和截面B1D1DB的距离是__________.
,且∠A1AD=∠A1AB=60°,则侧棱AA1和截面B1D1DB的距离是__________.
5、将半径为R的四个球,两两相切地放在桌面上,则上面的一个球的球心到桌面的距离为__________.
6、正三棱柱ABC-A1B1C1的所有棱长都为1,M、M1分别为棱BC、B1C1的中点,求直线AM与平面A1M1C的距离.
7、已知正三角形ABC的边长为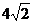 ,PA⊥平面ABC,PA=2,D、E、F分别是BC、DC、AC的中点,求直线AD到平面PEF的距离.
,PA⊥平面ABC,PA=2,D、E、F分别是BC、DC、AC的中点,求直线AD到平面PEF的距离.
8、在棱长为 的正方体ABCD-A1B1C1D1中,E、F、G分别是AA1、BC、CC1的中点,求顶点B1到平面EFG的距离.
的正方体ABCD-A1B1C1D1中,E、F、G分别是AA1、BC、CC1的中点,求顶点B1到平面EFG的距离.
高三数学教学案 第九章 立体几何
第十六课时 棱柱、棱锥的概念与性质
考纲摘录
了解棱柱、棱锥的概念;掌握棱柱、棱锥的性质,会画直棱柱,正棱锥的直观图.
知识概要
1、棱柱的定义、分类; 2、棱柱的主要性质; 3、平行六面体与长方体;
4、棱锥的定义、分类、性质; 5、正棱锥的概念、性质.
疑点难点
1、棱柱、棱锥是立体几何的重要载体;
2、三棱锥是最简单的棱锥,它的任一顶点都可以作为棱锥的顶点.
基础练习
1、具有下列性质的三棱锥中,哪一个是正三棱锥( )
A.顶点在底面的射影到底面各顶点的距离相等
B.底面是正三角形,且侧面都是等腰三角形
C.相邻两条侧棱间的夹角相等
D.三条侧棱相等,侧面与底面所成角也相等
2、下列命题中正确的是( )
A.有一个侧面是矩形的棱柱是直棱柱
B.有两个侧面是矩形的棱柱是直棱柱
C.有相邻两个侧面是矩形的棱柱是直棱柱
D.底面是正多边形的棱柱是直棱柱
3、一个棱柱是正四棱柱的条件是( )
A.底面是正方形,有两个侧面是矩形
B.底面是正方形,有两个侧面垂直于底面
C.底面是菱形,且有一个顶点处的三条棱两两垂直
D.每个侧面都是全等矩形的四棱柱
4、直四棱柱ABCD-A1B1C1D1的高为3,底面是边长为2的菱形且∠BAD=60°,F是A1D1的中点,则BF的长为( )
A.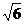 B.
B.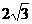 C.
C.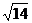 D.4
D.4
5、长方体的一条对角线与两组平行的面所成的角都是30°,则长方体的这条对角线与另一组平行的面所成的角是( )
A.45° B.60° C.30° D.45°或135°
例题讲解
例1、在四棱锥P-ABCD中,底面ABCD是边长为 的正方形,并且PD=
的正方形,并且PD= ,PA=PC=
,PA=PC=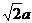
(1)求证:PD⊥平面ABCD;
(2)求异面直线PB与AC所成的角;
(3)求二面角A-PB-D的大小.

例2、斜三棱柱A1B1C1-ABC中,各棱长为 ,A1B= A1C=
,A1B= A1C=
 (1)求证:侧面BCC1B1是矩形;
(1)求证:侧面BCC1B1是矩形;
(2)求棱柱的高.
例3、棱长为1的正方体ABCD-A1B1C1D1,E是CC1的中点.
 (1)求证:平面B1DE⊥平面B1BD;
(1)求证:平面B1DE⊥平面B1BD;
(2)求二面B-B1E-D角的余弦值.
.
课后作业
班级_______学号__________姓名_________
1、有一条侧棱与底面的两条边垂直是棱柱成为直棱柱的一个________条件.
2、正三棱锥的侧面与底面成60°的二面角,则侧棱与底面所成角的正切值是__________.
3、长方体三度之和为 =6,全面积为11,则其对角线长为__________,若一条对角线与二个面所成的角为30°或45°,则与另一个面所成的角为_______,若一条对角线与各条棱所成的角为
=6,全面积为11,则其对角线长为__________,若一条对角线与二个面所成的角为30°或45°,则与另一个面所成的角为_______,若一条对角线与各条棱所成的角为 、
、 、
、 ,则
,则 、
、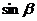 、
、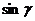 的关系为__________.
的关系为__________.
4、正四棱柱P-ABCD的高为PO,AB=2PO=2cm,则AB与侧面PCD的距离为( )
A.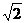 cm B.2cm C.
cm B.2cm C.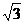 cm D.3cm
cm D.3cm
5、过正方体的每三个顶点都可确定一个平面,其中能与正方体的12条棱所成的角都相等的不同平面有________个.
6、已知正三棱柱ABC-A1B1C1中,AB=AA1,则直线CB1与平面AA1B1B所成角的正弦值为__________.
7、已知长方体ABCD-A1B1C1D1中,棱长AA1=5,AB=12,求直线B1C1和平面A1BCD1的距离.
8、四面体P-ABC中,已知PA=3,PB=PC=2,∠APB=∠CPA=60°;
求证:(1)PA⊥BC;
(2)平面PBC⊥平面ABC.
高三数学教学案 第九章 立体几何
第十七课时 棱柱、棱锥的侧面积与体积
考纲摘录
1、掌握直棱柱、正棱锥的侧面积及体积的公式;
2、掌握斜棱柱、一般棱锥的侧面积及体积的计算方法;
3、掌握棱锥的平行于底面的截面性质及简单运用.
知识概要
1、直棱柱的侧面积和体积公式; 2、斜棱柱的侧面积和体积公式;
3、棱锥的全面积; 4、正棱锥的侧面积公式; 5、棱锥的体积公式.
疑点难点
1、先证后算;
2、侧面展开图是研究侧面积的基础,是化空间的问题为平面问题的常用方法;
3、“割”与“补”,等积变形的应用.
基础练习
1、一个棱锥的所有侧面与底面所成角均为 ,底面积为S,则它的侧面积为________.
,底面积为S,则它的侧面积为________.
2、若棱锥的底面面积为8,则它的中截面面积是________.
3、侧面都是直角三角形的正三棱锥,底面边长为 ,则此棱锥的全面积等于( )
,则此棱锥的全面积等于( )
A.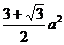 B.
B.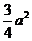 C.
C.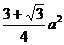 D.
D.
4、若斜三棱柱的高为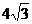 ,侧棱与底面所成的角为60°,相邻两侧棱之间的距离都为5,则该三棱柱的侧面积为( )
,侧棱与底面所成的角为60°,相邻两侧棱之间的距离都为5,则该三棱柱的侧面积为( )
A.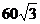 B.90 C.60 D.120
B.90 C.60 D.120
5、如果正方体ABCD-A1B1C1D1的棱长为 ,那么四面体A1-C1BD的体积为( )
,那么四面体A1-C1BD的体积为( )
A.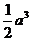 B.
B.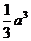 C.
C.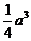 D.
D.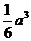
例题讲解
例1、斜棱柱A1B1C1-ABC底面是等腰△ABC,其边长分别是AB=AC=10cm,BC=12cm,棱柱的顶点A1与A、B、C三点等距,且侧棱AA1=13cm,求这棱柱的全面积.
例2、在三棱柱P-ABC中,PA、PB、PC两两成60°角,且PA= ,PB=
,PB=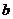 ,PC=
,PC=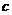 ,求三棱锥P-ABC的体积.
,求三棱锥P-ABC的体积.
例3、在直四棱柱ABCD-A1B1C1D1中,侧棱AA1= ,底面ABCD是边长AB=
,底面ABCD是边长AB= ,BC=
,BC= 的矩形,E为C1D1的中点,求三棱锥形B1-BDE的体积.
的矩形,E为C1D1的中点,求三棱锥形B1-BDE的体积.
课后作业
班级_______学号__________姓名_________
1、正六棱锥形底面边长为 ,体积为
,体积为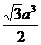 ,那么侧棱与底面所成的角等于( )
,那么侧棱与底面所成的角等于( )
A.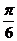 B.
B.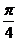 C.
C.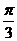 D.
D.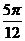
2、棱长都为1的正三棱锥的全面积为__________,体积为__________.
3、若正三棱锥形的全面积是底面积的4倍,则此正三棱锥侧面与底面所成的二面角等于( )
A.45° B.60° C.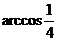 D.
D.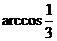
4、直三棱柱的各棱都相等,侧面积为36,则它的高为___________.
5、若一个锥体被平行于底面的平面所截,若截面面积是底面面积的四分之一,则锥体被截面截得的一个小棱锥与原棱锥体积之比为__________.
6、已知斜三棱柱ABC-A1B1C1各条棱长都是 ,且一个顶点A1在另一底面的射影恰好是这底面正三角形的中心,求此三棱柱的全面积.
,且一个顶点A1在另一底面的射影恰好是这底面正三角形的中心,求此三棱柱的全面积.
7、 如图,在斜三棱柱ABC-A1B1C1中,每条棱长都为
如图,在斜三棱柱ABC-A1B1C1中,每条棱长都为 ,侧棱与底面所成的角等于60°,其中侧面BCC1B1垂直于底面,求四棱锥C1-ABB1A1的体积.
,侧棱与底面所成的角等于60°,其中侧面BCC1B1垂直于底面,求四棱锥C1-ABB1A1的体积.
8、如图,四棱锥S-ABCD的底面ABCD是边长为 的正方形,SD⊥平面ABCD,平面ABEF与侧面SCD交于EF,二面角S-AB-C为45°,二面角F-AB-S为30°
的正方形,SD⊥平面ABCD,平面ABEF与侧面SCD交于EF,二面角S-AB-C为45°,二面角F-AB-S为30°
(1)求四边形ABEF的面积;
 (2)求棱锥S-ABEF的体积.
(2)求棱锥S-ABEF的体积.