
1、二面角、二面角平面角的定义;
2、两平面垂直的定义;
3、两平面垂直的判定定理;
4、两平面垂直的性质定理.
重点难点
“线线垂直”、“线面垂直”、“面面垂直”的相互转化.
基础练习
1、已知直线m、n,平面 、
、 ,且m⊥
,且m⊥ ,n
,n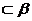 ,给出下列命题:①若
,给出下列命题:①若 ∥
∥ ,则
,则
m⊥n;②若m⊥n,则 ∥
∥ ;③若
;③若 ⊥
⊥ ,则m∥n;④若m∥n,则
,则m∥n;④若m∥n,则 ⊥
⊥ .其中正确的命题是( )
.其中正确的命题是( )
A.①④ B.①③ C.②③ D.③④
2、过平面 外两点且垂直平面
外两点且垂直平面 的平面( )
的平面( )
A.有且只有一个 B.有一个或两个
C.有且仅有两个 D.一个或无数个
3、已知PA⊥正方形ABCD所在的平面,垂足为A,连结PB、PC、PD、AC、BD,则互相垂直的平面有__________对.
4、两个平面互相垂直,一条直线和其中一个平面平行,则这条直线与另一个平面的位置关系是__________________ ____.
例题讲解
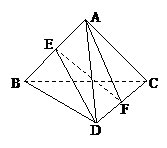
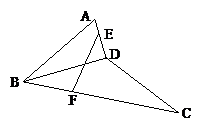
例1、在三棱锥A-BCD中,AB=3,AC=AD=2,且∠DAC=∠BAC=∠BAD=60°,
 求证:平面BCD⊥平面ADC.
求证:平面BCD⊥平面ADC.
例2、如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1,CD的中点.
 求证:平面AED⊥平面A1FD1.
求证:平面AED⊥平面A1FD1.
例3、已知平面PAB⊥平面ABC,平面PAC⊥平面ABC,E是点A在平面PBC内的射影,
(1)求证:PA⊥平面ABC;(2)当E为△PBC的垂心时,求证:△ABC是直角三角形.
课后作业
班级_______学号__________姓名_________
1、平面 ⊥平面
⊥平面 ,
, ∩
∩ =
= ,点P∈
,点P∈ ,点Q∈
,点Q∈ ,那么PQ⊥
,那么PQ⊥ 是PQ⊥
是PQ⊥ 的(
)
的(
)
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分也不必要条件
2、已知平面PAB、PBC、PAC两两互相垂直,点P在面ABC上的射影为O,则O是△ABC的( )
A.内心 B.外心 C.垂心 D.重心
3、若 、m是互相不垂直的异面直线,平面
、m是互相不垂直的异面直线,平面 、
、 分别过
分别过 、m,则下列关系中不可能成立的是( )
、m,则下列关系中不可能成立的是( )
A. ∥
∥ B.
B. ∥
∥ 且m∥
且m∥ C.
C. ⊥
⊥ D.
D. ⊥
⊥ 且m⊥
且m⊥
4、在直二面角 -
- -
- 中,A∈
中,A∈ ,B∈
,B∈ ,AB=2,AB与
,AB=2,AB与 、
、 所成角分别为30°和45°,则点A、B在
所成角分别为30°和45°,则点A、B在 上的射影A′,B′间的距离是________ __.
上的射影A′,B′间的距离是________ __.
5、在矩形ABCD中,AB=3,BC=4,沿BD将该矩形折成直二面角,那么折后A、C两点间的距离为__________.
6、在正方体ABCD-A1B1C1D1中,E是CC1的中点,求证:平面BDE⊥平面A1BD.

7、如图S为△ABC所在平面外一点SA=SB=SC,且∠ABC=90°,
求证:平面SAC⊥平面ABC.

8、在三棱锥P-ABC中,PB=PC,AB=AC,点D为BC中点,AH⊥PD于H点,连BH,
求证:平面ABH⊥平面PBC.

高三数学教学案 第九章 立体几何
第八课时 平面与平面垂直(二)
目标要求
熟练掌握面面垂直的有关知识,并能综合运用有关知识解决问题.
基础练习
1、对于直线m、n和平面 、
、 ,
, ⊥
⊥ 的一个充分条件是
( )
的一个充分条件是
( )
A.m⊥n,m∥ ,n∥
,n∥ B.m⊥n,
B.m⊥n, ∩
∩ =m,n
=m,n
C.m∥n,n⊥ ,m
,m D.m∥n,m⊥
D.m∥n,m⊥ ,n⊥
,n⊥
2、设X、Y、Z是空间不同的直线或平面,对下面四种情形,使“X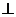 Z且Y
Z且Y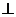 Z
Z  X//
Y”
为真命题的是______
__.
X//
Y”
为真命题的是______
__.
①X、Y、Z是直线; ②X、Y是直线,Z是平面;③Z是直线,X、Y是平面; ④X、Y、Z是平面.
3、 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,
底面各边都相等,M是PC上的一动点,当点M满
足_______ __时,平面MBD⊥平面PCD.
(只需写出一种情形)
例题讲解
例1、如图,ABCD是边长为 的菱形,∠A=60°,PC⊥平面ABCD,PC=
的菱形,∠A=60°,PC⊥平面ABCD,PC= ,E是PA的中点,(1)求证:平面BDE⊥平面ABCD;(2)求E到平面PBC的距离.
,E是PA的中点,(1)求证:平面BDE⊥平面ABCD;(2)求E到平面PBC的距离.

例2、正三棱柱ABC-A1B1C1的底面边长为 ,侧棱长为
,侧棱长为 .若经过对角线AB1且与对角线BC1平行的平面交上底面于DB1. (1)试确定点D的位置,并加以证明;
.若经过对角线AB1且与对角线BC1平行的平面交上底面于DB1. (1)试确定点D的位置,并加以证明;
(2)求证:平面AB1D⊥平面ACC1A1.

例3、如图,ABCD是正方形,E、F分别是AD、BC上的点,EF∥AB,EF交AC于点O,以EF为棱把它折成直二面角A-EF-D后,求证:不论EF怎样移动,∠AOC是定值.

课后作业
班级_______学号__________姓名_________
1、若直线 、m与平面
、m与平面 、
、 、
、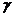 满足:
满足: ∩
∩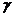 =
= ,
, ∥
∥ ,m
,m ,m⊥
,m⊥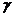 ,则有(
)
,则有(
)
A. ⊥
⊥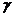 ,
, ⊥m B.
⊥m B. ⊥
⊥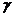 ,m∥
,m∥
C.m∥ ,
, ⊥m D.
⊥m D. ∥
∥ ,
, ⊥
⊥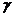
2、若平面 ⊥平面
⊥平面 ,直线n
,直线n ,直线m
,直线m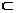
 ,m⊥n,则
( )
,m⊥n,则
( )
A.n⊥ B.n⊥
B.n⊥ 且m⊥
且m⊥
C.m⊥ D.n⊥
D.n⊥ 与m⊥
与m⊥ 中至少有一个成立
中至少有一个成立
3、三个平面两两垂直,它们的三条交线交于一点O,P点到三个平面的距离分别是3,4,5,则OP的长为___________.
4、若有平面 与
与 ,
, ∩
∩ =
= ,
, ⊥
⊥ ,P∈
,P∈ ,P
,P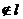 ,则下列命题中,真命题有_______个.
,则下列命题中,真命题有_______个.
①过点P且垂直于 的直线平行于
的直线平行于 ; ②过点P且垂直于
; ②过点P且垂直于 的平面垂直于
的平面垂直于 ;
;
③过点P且垂直于 的直线在
的直线在 内; ④过点P且垂直于
内; ④过点P且垂直于 的直线在
的直线在 内.
内.
5、矩形ABCD,ABEF所在平面互相垂直,且AB=4,AD=2,AF=3,∠AED= ,∠EDC=
,∠EDC= ,则
,则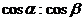 =__________
=__________
6、若V是△ABC所在平面外一点,VB⊥平面ABC,平面VAB⊥平面VAC,
求证:△ABC是直角三角形.

7、ABC-A1B1C1是正三棱柱,底面边长为 ,D、E分别是BB1、CC1上的点,BD=
,D、E分别是BB1、CC1上的点,BD= ,EC=
,EC= .(1)求证:平面ADE⊥平面ACC1A1;(2)求截面△ADE的面积.
.(1)求证:平面ADE⊥平面ACC1A1;(2)求截面△ADE的面积.

8、如图,四棱锥P-ABCD中,底面ABCD是菱形,并且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD.
(1)求证:AD⊥PB;
(2)设E为BC边的中点,F为PC中点,求证:平面DEF⊥平面ABCD.

高三数学教学案 第九章 立体几何
第九课时 异面直线所成的角
考纲摘录
掌握空间两条直线所成角的概念.
知识概要
1、异面直线所成角的定义,异面直线所成角的范围;
2、求异面直线所成角的大小,一般方法是通过平移直线,把异面直线问题化为共面问题解决.
重点难点
如何平移,从而转化为相交直线所成角并能求出该角.
基础练习
1、已知异面直线 ,
,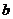 所成的角为60°,P为空间一定点,则过点P且与
所成的角为60°,P为空间一定点,则过点P且与 ,
,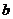 所成角都是60°的直线有且仅有
( )
所成角都是60°的直线有且仅有
( )
A.1条 B.2条 C.3条 D.4条
2、棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是A1B1和BB1的中点,则直线AM与CN所成角的余弦值是 ( )
A. B.
B.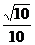 C.
C. D.
D.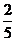
3、在空间四边形ABCD中,AD=BC=2,E,F分别是AB,CD的中点,EF=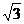 ,则AD,BC所成角为_________.
,则AD,BC所成角为_________.
4、已知 、
、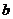 是两条异面直线,AB是其公垂线,垂足分别是A、B,M∈
是两条异面直线,AB是其公垂线,垂足分别是A、B,M∈ ,N∈
,N∈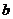 ,AB=4,AM=3,BN=2,MN=
,AB=4,AM=3,BN=2,MN=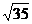 ,则
,则 与
与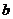 所成的角为_________.
所成的角为_________.
例题讲解
例1、如图,在三棱锥D-ABC中,DA⊥平面ABC,∠ACB=90°,∠ABD=30°,AC=BC,求异面直线AB与CD所成角的余弦值.

例2、如图,正三棱柱ABC-A1B1C1的底面边长为8,对角线B1C=10,D为AC中点,
(1)求证:AB1∥平面C1BD;(2)求异面直线AB1与BC1所成的角.

例3、如图,在直四棱柱ABCD-A1B1C1D1中,底面是边长为1的菱形,侧棱长为2,
(1)B1D1与A1D能否垂直?请证明你的判断.
(2)当∠A1B1C1在 上变化时,求异面直线AC1与A1B1所成角的取值范围.
上变化时,求异面直线AC1与A1B1所成角的取值范围.

课后作业
班级_______学号__________姓名_________
1、在正方体ABCD-A1B1C1D1中,表面的对角线中与AD1成60°角的有_______条.
2、已知空间四边形ABCD中,AC、BD成60°角,且AC=4,BD= ,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的面积为__________.
,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的面积为__________.
3、长方体ABCD-A1B1C1D1中,已知BB1=BC=1,AB=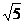 ,则异面直线DB1与BC1所成角为___________.
,则异面直线DB1与BC1所成角为___________.
4、在正三棱锥A-BCD中,E、F分别为棱AB、CD的中点,设EF与AC所成的角为 ,EF与BD所成的角为
,EF与BD所成的角为 ,则
,则 +
+ 等于( )
等于( )
A.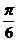 B.
B.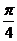 C.
C.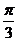 D.
D.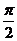
5、在正四面体ABCD中,E、F分别是AB、CD的中点, 求:(1)异面直线EF与AC所成角的大小; (2)异面直线AF与DE所成角的大小.
6、如图所示,空间四边形ABCD中,两条对边AB=CD=3,E、F分别是另外两条对边AD、BC上的点,且AE:ED = BF:FC=1:2,EF= ,求AB和CD所成角的大小.
,求AB和CD所成角的大小.
7、如图,长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,E、H分别是A1B1和BB1的中点,求:(1)EH与AD1所成的角;(2)AC1与B1C所成的角.

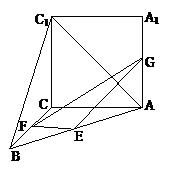
8、如图,正方形ACC1A1与等腰直角△ACB所在平面互相垂直,且AC=BC=2,E、F、G分别是线段AB、BC、AA1的中点.
(1)判断直线C1B与平面EFG的位置关系,并说明理由;
(2)求异面直线AC1与GF所成角的大小.
高三数学教学案 第九章 立体几何
第十课时 直线与平面所成的角
考纲摘录
掌握直线与平面所成角的概念.
知识概要
1、斜线与平面所成角的定义,空间直线与平面所成角的范围;
2、求直线与平面所成角的关键是作垂直,找射影.
重点难点
如何作垂直定射影,以而构成直角三角形,并能够求出角.
基础练习
1、两条直线 ,
,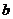 与平面
与平面 所成的角相等,则
所成的角相等,则 ,
,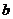 的位置关系是( )
的位置关系是( )
A.平行 B.相交 C.异面 D.以上均可能
2、若线段AB夹在两个互相垂直的平面 、
、 间,AB与
间,AB与 成
成 角,AB与
角,AB与 成
成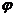 角,则
角,则 +
+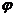 的值的范围( )
的值的范围( )
A.0°< +
+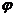 ≤90° B.0°<
≤90° B.0°< +
+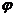 <
90°
<
90°
C.90°≤ +
+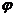 <180° D.以上都不对
<180° D.以上都不对
3、∠AOB在平面 内,OC是
内,OC是 的斜线,OB为OC在平面
的斜线,OB为OC在平面 内的射影,若∠COA=
内的射影,若∠COA= ,∠COB=
,∠COB= 1,∠BOA=
1,∠BOA= 2,则
2,则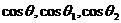 三者之间满足的关系式是___________.
三者之间满足的关系式是___________.
4、已知正方体ABCD-A1B1C1D1中,E为AD的中点,则ED1与平面AA1C1C所成的角的正弦值是_________.
例题讲解
 例1、如图,在正方体AC1中,(1)求BC1与平面ACC1A1所成的角; (2)求A1B1与平面A1C1B所成的角.
例1、如图,在正方体AC1中,(1)求BC1与平面ACC1A1所成的角; (2)求A1B1与平面A1C1B所成的角.
例2、已知二面角 -
- -
- 为60°,
为60°, 上有两点A、B,线段AC,BD分别在面
上有两点A、B,线段AC,BD分别在面 、
、 内,且AC⊥AB,BD⊥AB,AB=4,AC=6,BD=8,
内,且AC⊥AB,BD⊥AB,AB=4,AC=6,BD=8,
(1)求CD的长; (2)求异面直线CD与AB所成的角;
(3)求CD与平面 所成的角.
所成的角.

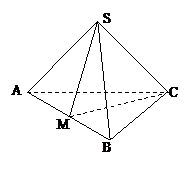
例3、在四面体S-ABC中,SA,SB,SC两两垂直,∠SBA=45°,∠SBC=60°,M为AB的中点,求(1)BC与平面SAB所成角; (2)SC与平面ABC所成角.
课后作业
班级_______学号__________姓名_________
1、在正方体ABCD-A1B1C1D1中,A1B与平面BB1D1D所成角的大小是_________.
2、有一个三角尺ABC,∠A=30°,∠C=90°,BC贴于桌面上,当三角尺与桌面成45°角时,AB边与桌面所成角的正弦值是__________.
3、已知一个平面与一个正方体的十二条棱所成的角均为 ,则
,则 ___________.
___________.
4、平面 的斜线与
的斜线与 所成的角为30°,则此斜线和
所成的角为30°,则此斜线和 内所有不过斜足的直线所成角的最大值是( )
内所有不过斜足的直线所成角的最大值是( )
A.30° B.60° C.90° D.150°
5、在正四面体ABCD中,E为棱AD中点,则CE与平面BCD所成角的正弦值为__________.
6、已知平面 与
与 所成的二面角为80°,P为
所成的二面角为80°,P为 、
、 外一定点,过点P的一条直线与
外一定点,过点P的一条直线与 、
、 所成的角为30°,则这样的直线有且仅有( )
所成的角为30°,则这样的直线有且仅有( )
A.1条 B.2条 C.3条 D.4条
7、已知∠BOC在平面 内,OA是
内,OA是 的斜线,若∠AOB=AOC=60°,OB=OC=
的斜线,若∠AOB=AOC=60°,OB=OC= ,BC=
,BC=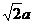 ,求OA和平面
,求OA和平面 所成的角.
所成的角.
7、在三棱柱ABC-A1B1C1中,四边形A1ABB1是菱形,四边形BCC1B1是矩形,
 C1B1⊥AB.(1)求证:平面CA1B⊥A1AB;(2)若C1B1=3,AB=4,∠ABB1=60°,求AC1与平面BCC1所成角的大小.
C1B1⊥AB.(1)求证:平面CA1B⊥A1AB;(2)若C1B1=3,AB=4,∠ABB1=60°,求AC1与平面BCC1所成角的大小.
8、如右图,在三棱锥P-ABC中,AB⊥BC,AB=BC=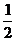 PA,点O、D分别是AC、PC的中点,OP⊥底面ABC, (1)求证:OD∥平面PAB;
PA,点O、D分别是AC、PC的中点,OP⊥底面ABC, (1)求证:OD∥平面PAB;
(2)求直线OD与平面PBC所成角的大小.

高三数学教学案 第九章 立体几何
第十一课时 二面角(一)
考纲摘录
掌握平面与平面所成角的概念,能正确画出两个平面位置关系的图形,并能运用二面
角及其平面角的概念进行计算和证明.
知识概要
1、二面角,二面角的平面角的定义;
2、二面角的平面角的三种作法;
3、求二面角大小时一般按“一作,二证,三计算”步骤进行.
重点难点
重点是在具体问题中如何作出平面角,并能求出该角,比较困难的是求没有给出的棱的二面角大小.
基础练习
1、从点P出发引三条射线PA、PB、PC,每两条的夹角都是60°,则二面角B-PA-C的余弦值是 ( )
A.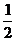 B.
B.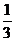 C.
C.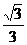 D.
D.
2、已知二面角 -
- -
- 为60°,若平面
为60°,若平面 内有一点A到平面
内有一点A到平面 的距离为
的距离为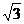 ,那么A在平面
,那么A在平面 上的射影A1到平面
上的射影A1到平面 的距离为 ( )
的距离为 ( )
A. B.1 C.
B.1 C.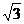 D.
D.
3、锐二面角 -
- -
- 中,AB
中,AB ,AB与
,AB与 成45°角,与
成45°角,与 成30°角,则二面角的大小为__________.
成30°角,则二面角的大小为__________.
4、 若正三棱锥的一个侧面的面积与底面面积的比等于
若正三棱锥的一个侧面的面积与底面面积的比等于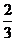 ,则这个三棱锥的侧面和底面所成的二面角的大小为_________.
,则这个三棱锥的侧面和底面所成的二面角的大小为_________.
例题讲解
例1、正方体ABCD-A1B1C1D1的棱长为a,P,Q,R分别
为棱AA1,AB,BC的中点, (1)求证:∠PQR为钝角;
(2)求二面角P-QR-A的正弦值.
 例2、在直三棱柱ABC-A1B1C1中,底面三角形ABC为等腰直角三角形且∠ABC=90°,E为C1C的中点,F在BB1上,且BF=
例2、在直三棱柱ABC-A1B1C1中,底面三角形ABC为等腰直角三角形且∠ABC=90°,E为C1C的中点,F在BB1上,且BF= BB1,BB1=BC,求平面EFA与面ABC所成角的大小.
BB1,BB1=BC,求平面EFA与面ABC所成角的大小.
例3、已知斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC,A1在底面ABC的射影恰为AC的中点M,又知AA1与底面ABC所成的角为60°,(1)求证:BC⊥平面AA1C1C;
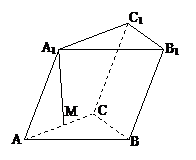 (2)求二面角B-AA1-C的大小.
(2)求二面角B-AA1-C的大小.
课后作业
班级_______学号__________姓名_________
1、在正四棱锥中相邻两侧面所成的二面角一定是 ( )
A.锐角 B.直角 C.钝角 D.均有可能
2、在二面角 -
- -
- 内,过
内,过 作一个半平面
作一个半平面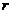 , 使二面角
, 使二面角  -
- -
- 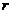 的大小为
的大小为
45°,二面角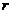 -
- -
- 的大小为30°,则
的大小为30°,则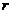 内任一点P到平面
内任一点P到平面 与平面
与平面 的距离之比为
( )
的距离之比为
( )
A. B.
B. C.
C. D.
D.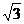
3、正方体ABCD-A1B1C1D1中,二面角B1-AA1-C1的大小为____________,二面角B-A1C-A的大小为________.
4、已知直角△ABC的斜边AB在平面 内,AC、BC分别与
内,AC、BC分别与 成30°、45°角,则
成30°、45°角,则 与△ABC所在平面所成的二面角的度数为________.
与△ABC所在平面所成的二面角的度数为________.
5、如图,过正方形ABCD的顶点A引PA⊥平面ABCD,若PA=AB,则平面ABP和平面CDP所成的二面角的大小为__________.
6、在正三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=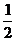 AB,这时二面角B-AD-C的大小为_________.
AB,这时二面角B-AD-C的大小为_________.
7、在四面体ABCD中,BD=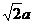 ,其余各棱长均为
,其余各棱长均为 ,求二面角A-BD-C,
,求二面角A-BD-C,
 A-BC-D,B-AC-D的大小.
A-BC-D,B-AC-D的大小.
8、如图,斜三棱柱ABC-A1B1C1中,AB=BB1,BB1与底面成60°角,侧面A1B⊥底面ABC,△ABC是正三角形.
(1)证明:AB⊥B1C;
(2)证明:B1C⊥平面ABC1;
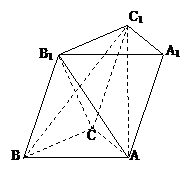 (3)求二面角B1-AC-B的大小.
(3)求二面角B1-AC-B的大小.