
1、椭圆 的长轴位于_________轴,长轴长等于_________;短轴位于_________轴,短半轴长等于_________;焦点在_________轴上,焦点坐标分别为_________
的长轴位于_________轴,长轴长等于_________;短轴位于_________轴,短半轴长等于_________;焦点在_________轴上,焦点坐标分别为_________
_________,离心率 ,准线方程为_________;焦点到相应准线的距离(焦准距)等于_________;左顶点坐标为_________;下顶点的坐标是_________.椭圆上点
,准线方程为_________;焦点到相应准线的距离(焦准距)等于_________;左顶点坐标为_________;下顶点的坐标是_________.椭圆上点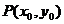 的横坐标范围是
的横坐标范围是 ,纵坐标的范围是
,纵坐标的范围是 ;
; 的取值范围是______________.
的取值范围是______________.
2、已知M、N的坐标分别为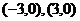 ,(1)若|PM|+|PN|=6,则P的轨迹方程为_____________;(2)若△PMN的周长为16,则点P的轨迹方程为__________________.
,(1)若|PM|+|PN|=6,则P的轨迹方程为_____________;(2)若△PMN的周长为16,则点P的轨迹方程为__________________.
3、已知椭圆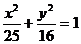 上一点M(1)若M(4,2.4),则M与两个焦点的距离分别为___________;(2)若M到一个焦点的距离为3,则它到相应准线的距离等于_________,到另一条准线的距离为_________,到另一焦点的距离等于_________.
上一点M(1)若M(4,2.4),则M与两个焦点的距离分别为___________;(2)若M到一个焦点的距离为3,则它到相应准线的距离等于_________,到另一条准线的距离为_________,到另一焦点的距离等于_________.
4、椭圆 的离心率
的离心率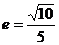 ,则
,则 值为______________.
值为______________.
5、椭圆满足下列条件之一,求离心率(1)一个焦点将长轴分成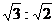 两段,
两段, ;(2)焦点与短轴的两个端点的连线互相垂直,
;(2)焦点与短轴的两个端点的连线互相垂直, ;(3)两焦点与一个顶点恰构成一个等边三角形,
;(3)两焦点与一个顶点恰构成一个等边三角形, .
.
例题讲解
例1、已知椭圆的中心在原点,焦点在坐标轴上,长轴长是短轴长的3倍,且过点P(3,2),求椭圆的方程.
例2、已知椭圆的一条准线方程是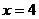 ,且过点
,且过点 ,求椭圆的标准方程.
,求椭圆的标准方程.
例3、设 、
、 为
为 椭圆的两个焦点,
椭圆的两个焦点,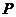 为椭圆上的一点,已知
为椭圆上的一点,已知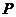 、
、 、
、 是一个直角三角形的三个顶点,且|
是一个直角三角形的三个顶点,且|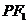 |>|
|>|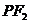 |,求
|,求 的值.
的值.
例4、若已知椭圆 ,P为椭圆上的一点,且
,P为椭圆上的一点,且 ,求
,求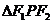 的面积.
的面积.
课后作业
班级_______学号__________姓名_________
1、椭圆的短轴长是2,长轴是短轴的2倍,则椭圆的中心到其准线的距离为( )
A. B.
B.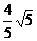 C.
C. D.
D.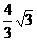
2、如果方程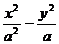 =1表示焦点在
=1表示焦点在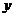 轴上的椭圆,则实数
轴上的椭圆,则实数 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C. D.以上都不对
D.以上都不对
3、椭圆 上的点
上的点 到左焦点的距离
到左焦点的距离 到右准线的距离为___________.
到右准线的距离为___________.
4、椭圆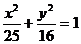 的左、右焦点为
的左、右焦点为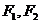 ,P在椭圆上,且
,P在椭圆上,且 ,则
,则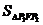 =___________.
=___________.
5、已知椭圆 ,A为左顶点,B为短轴的一顶点,F为右焦点,且
,A为左顶点,B为短轴的一顶点,F为右焦点,且 则此椭圆的离心率为__________.
则此椭圆的离心率为__________.
6、P为椭圆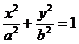 上的一点,
上的一点, ,
, 为焦点,如果
为焦点,如果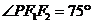 ,
, ,则椭圆的离心率为__________.
,则椭圆的离心率为__________.
7、P为椭圆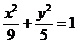 上异于长轴端点的点,
上异于长轴端点的点, 、
、 为左,右两焦点,过
为左,右两焦点,过 作
作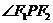 外角平分线的垂线,垂足为M,则M的轨迹方程为__________.
外角平分线的垂线,垂足为M,则M的轨迹方程为__________.
8、根据下列条件,求椭圆的标准方程
(1)两准线间的距离为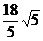 ,焦距为
,焦距为 ;
;
(2)和椭圆 共准线,且离心率为
共准线,且离心率为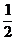 .
.
9、(选做题)
已知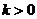 ,直线
,直线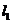 :
: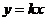 ,
,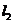 :
:
(1)证明:到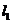 ,
,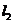 的距离的平方和为定值
的距离的平方和为定值 的点的轨迹是圆或椭圆
的点的轨迹是圆或椭圆
(2)若(1)中轨迹是椭圆,且该椭圆的离心率等于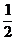 ,求
,求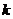 的值.
的值.
高三数学教学案 第八章 圆锥曲线
第二课时 椭圆(二)
考纲摘录
运用椭圆的定义、性质解决相关问题.
基础练习
1、若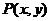 是椭圆
是椭圆 上的点,则
上的点,则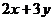 的值域为______________.
的值域为______________.
2、设P为椭圆 上的点,
上的点, (
(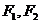 为两焦点),则
为两焦点),则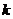 的最大值与最小值的差为__________________.
的最大值与最小值的差为__________________.
3、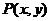 为椭圆
为椭圆 上的点,则点P到直线
上的点,则点P到直线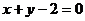 的最大距离为_________.
的最大距离为_________.
4、若椭圆的两准线之间的距离不大于长轴长的3倍,则它的离心率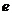 的范围为______________.
的范围为______________.
例题讲解
例1、若椭圆 上存在一点M,使
上存在一点M,使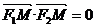 ,求椭圆离心率的范围.
,求椭圆离心率的范围.
例2、已知F是椭圆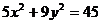 的左焦点,P是椭圆上的动点,A(1,1)是一定点
的左焦点,P是椭圆上的动点,A(1,1)是一定点
(1)求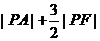 的最小值,并求P的坐标;
的最小值,并求P的坐标;
(2)求 的最大值与最小值.
的最大值与最小值.
例3、已知椭圆 ,长轴的两端点为A、B,如果椭圆上存在一点Q,使∠AQB=120°,求椭圆离心率的取值范围.
,长轴的两端点为A、B,如果椭圆上存在一点Q,使∠AQB=120°,求椭圆离心率的取值范围.
例4、已知椭圆的中心在原点,离心率为 ,一个焦点为F
,一个焦点为F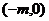 (
( 为大于0的常数)
为大于0的常数)
(1)求椭圆方程;
(2)设 为椭圆上的一点,过点F、
为椭圆上的一点,过点F、 的直线
的直线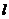 与
与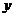 轴交于点M,若
轴交于点M,若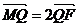 ,求
,求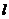 直线的斜率.
直线的斜率.
课后作业
班级_______学号__________姓名_________
1、若椭圆 内有一点
内有一点 ,F为右焦点,椭圆上有一点M,使|MP|+2|MF|的最小,则M的值为( )
,F为右焦点,椭圆上有一点M,使|MP|+2|MF|的最小,则M的值为( )
A.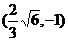 B.
B. C.
C.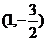 D.
D.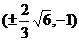
2、设P为椭圆上一点,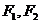 为两焦点,
为两焦点,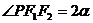 ,
,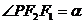 (
(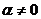 ),那么离心率为( )
),那么离心率为( )
A.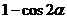 B.
B.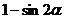 C.
C.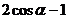 D.
D.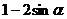
3、椭圆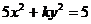 的一个焦点为(0,2),则
的一个焦点为(0,2),则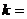 ___________.
___________.
4、椭圆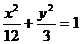 的左、右焦点为
的左、右焦点为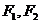 点P在椭圆上,若线段
点P在椭圆上,若线段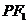 的中点在
的中点在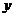 轴上,则
轴上,则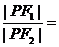 ___________.
___________.
5、一个椭圆的离心率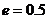 ,准线方程为
,准线方程为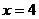 ,对应的焦点为F(2,0),则该椭圆的中心为__________,椭圆的方程为____________________.
,对应的焦点为F(2,0),则该椭圆的中心为__________,椭圆的方程为____________________.
6、如图,在△AFB中,∠AFB=150°,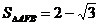 ,一个椭圆以F为一个焦点,以A,B分别作为长、短轴的一个端点,以原点O作为中心,求该椭圆的方程.
,一个椭圆以F为一个焦点,以A,B分别作为长、短轴的一个端点,以原点O作为中心,求该椭圆的方程.
7、如图△ 的面积为S,且
的面积为S,且 =1.(1)若
=1.(1)若 ,求向量
,求向量 与
与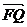 的夹角
的夹角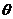 的取值范围,(2)设
的取值范围,(2)设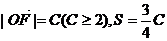 ,若以O为中心,F为焦点的椭圆经过点
,若以O为中心,F为焦点的椭圆经过点 ,当
,当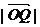 取得最小值时,求此椭圆的方程.
取得最小值时,求此椭圆的方程.
8、(选做题)
设椭圆的中心是坐标原点,长轴在 轴上,离心率
轴上,离心率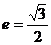 ,已知
,已知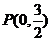 到这个椭圆上的点的最远距离为
到这个椭圆上的点的最远距离为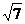 ,求这个椭圆的方程.
,求这个椭圆的方程.
高三数学教学案 第八章 圆锥曲线
第三课时 双曲线(一)
考纲摘录
掌握双曲线的定义,标准方程和双曲线的简单几何性质.
知识概要
双曲线定义的两种形式,标准方程的两种情形,几何量a,b,c,e,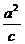 等之间的关系;特征三角形;渐近线等.
等之间的关系;特征三角形;渐近线等.
重点、难点
双曲线的性质及应用,双曲线标准方程的求解方法.
基础练习
1、双曲线 的实轴在_________轴上,虚轴在_________轴上,实轴长等于_________,虚半轴长等于____________,焦距等于____________,顶点坐标是___________,焦点坐标是_________,准线方程是_________________,渐近线方程是_______________,离心率
的实轴在_________轴上,虚轴在_________轴上,实轴长等于_________,虚半轴长等于____________,焦距等于____________,顶点坐标是___________,焦点坐标是_________,准线方程是_________________,渐近线方程是_______________,离心率 ,若点
,若点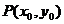 是双曲线上的点,则
是双曲线上的点,则 ,
, .
.
2、双曲线 的左支上一点到左焦点的距离是7,则这点到双曲线右焦点的距离是( )
的左支上一点到左焦点的距离是7,则这点到双曲线右焦点的距离是( )
A.13 B.13或1 C.10 D.10或4
3、已知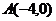 ,
, ,(1)若
,(1)若 ,则动点
,则动点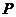 的轨迹方程为__________________,(2)若
的轨迹方程为__________________,(2)若 则动点
则动点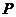 的轨迹方程为________________,(3)若△ABC中,
的轨迹方程为________________,(3)若△ABC中,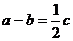 (a,b,c,为
(a,b,c,为 、
、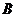 、
、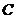 的对边),则点C的轨迹轨迹为_____________________.
的对边),则点C的轨迹轨迹为_____________________.
4、过双曲线 的右焦点作
的右焦点作 轴的垂线交双曲线于
轴的垂线交双曲线于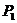 、
、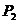 两点,则
两点,则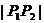 =______________(用a,b表示).
=______________(用a,b表示).
5、若双曲线 的一个焦点是(0,4),则
的一个焦点是(0,4),则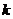 等于__________.
等于__________.
6、双曲线的渐近线方程是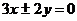 ,则其离心率为__________.
,则其离心率为__________.
例题讲解
例1、根据下列条件求双曲线的标准方程.
(1)与双曲线 共同的渐近线,且过点(2,2);
共同的渐近线,且过点(2,2);
(2)一条渐近线方程为 ,一条准线方程为
,一条准线方程为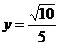 ;
;
(3)经过两点 ,
,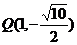 ;
;
(4)焦距为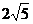 ,顶点到渐近线的距离为
,顶点到渐近线的距离为 .
.
例2、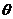 为△ABC的内角,就
为△ABC的内角,就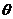 的不同取值,讨论方程
的不同取值,讨论方程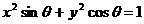 所表示的曲线的形状.
所表示的曲线的形状.
例3、有一个椭圆,中心是坐标原点,两焦点在 轴上,焦距为
轴上,焦距为 ,一双曲线和这个椭圆有公共焦点,且双曲线的实半轴长比椭圆的长半轴长小4,双曲线的离心率与椭圆的离心率之比为7:3,求它们的方程.
,一双曲线和这个椭圆有公共焦点,且双曲线的实半轴长比椭圆的长半轴长小4,双曲线的离心率与椭圆的离心率之比为7:3,求它们的方程.
班级_______学号__________姓名_________
课后作业
1、双曲线 的两条准线方程是( )
的两条准线方程是( )
A. B.
B.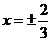 C.
C.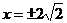 D.
D.
2、已知点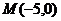 ,
,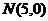 给出下列直线方程:
给出下列直线方程:
① ②
② ③
③ ④
④ 则在直线上存在点P满足
则在直线上存在点P满足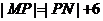 的所有直线方程为( )
的所有直线方程为( )
A. ①④ B. ②④ C.②③ D.①③
3、曲线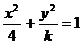 的离心率
的离心率 则实数
则实数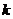 的取值范围是____________.
的取值范围是____________.
4、若双曲线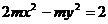 的一条准线为
的一条准线为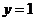 ,则
,则 _______________.
_______________.
5、设过双曲线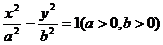 的焦点
的焦点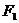 且交双曲线于同一支的弦为AB,另一焦点为
且交双曲线于同一支的弦为AB,另一焦点为 ,若
,若 的周长为
的周长为 ,则
,则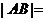 ____________.
____________.
6、双曲线的中心在坐标原点,焦点在 轴上,
轴上,
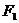 、
、 为左、右两焦点,双曲线右支上有一点
为左、右两焦点,双曲线右支上有一点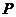 ,
,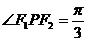 ,
, ,离心率为2,求双曲线方程.
,离心率为2,求双曲线方程.
7、椭圆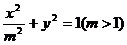 与双曲线
与双曲线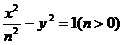 有公共焦点
有公共焦点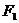 ,
, ,P为两曲线的一个交点,求
,P为两曲线的一个交点,求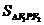 .
.
8、(选做题)
直线 :
: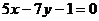 与以坐标轴对称的曲线C交于A、B两点,点P(5,14)与A、B构成以AB为斜边的等腰直角三角形,求双曲线C的方程.
与以坐标轴对称的曲线C交于A、B两点,点P(5,14)与A、B构成以AB为斜边的等腰直角三角形,求双曲线C的方程.
高三数学教学案 第八章 圆锥曲线
第四课时 双曲线(二)
目标要求
运用双曲线的定义、性质解决相关问题.
基础练习
1、已知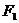 ,
, 为双曲线
为双曲线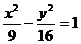 的左、右两个焦点,P为左支上任一点则
的左、右两个焦点,P为左支上任一点则 ,
, .
.
2、若双曲线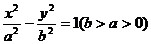 的渐近线所夹的锐角为
的渐近线所夹的锐角为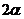 ,则它的离心率为( )
,则它的离心率为( )
A. B.
B.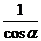 C.
C. D.
D.
3、已知双曲线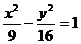 的右焦点F,点A(9,2)试在曲线上求一点M,使|MA|+
的右焦点F,点A(9,2)试在曲线上求一点M,使|MA|+ |MF|值最小,则M为___________,最小值为____________.
|MF|值最小,则M为___________,最小值为____________.
4、设动点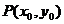 在定双曲线
在定双曲线 上运动,
上运动,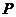 到两条渐近线的距离分别为
到两条渐近线的距离分别为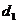 ,
,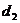 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.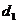 +
+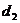 为定值 B.|
为定值 B.|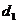 -
-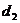 |为定值
|为定值
C.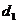
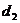 为定值 D.
为定值 D.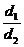 为定值
为定值
5、若焦点在 轴上的双曲线
轴上的双曲线 上的一条准线为圆
上的一条准线为圆 的一条切线,则
的一条切线,则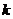 =__________.
=__________.
6、双曲线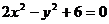 上一点P到一个焦点的距离为4,则点P到较远的准线的距离为_____________.
上一点P到一个焦点的距离为4,则点P到较远的准线的距离为_____________.
7、已知双曲线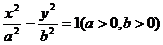 ,直线
,直线 过点
过点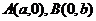 ,左焦点
,左焦点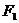 到直线
到直线 的距离等于该双曲线虚轴长的
的距离等于该双曲线虚轴长的 .
.
(1)求双曲线的离心率;
(2)若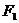 到左准线的距离与它到渐近线的距离和是
到左准线的距离与它到渐近线的距离和是 ,求双曲线方程.
,求双曲线方程.
8、双曲线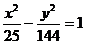 的左、右焦点分别为
的左、右焦点分别为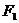 ,
, ,左准线为
,左准线为 ,能否在双曲线的左半支上找到一点P,使得
,能否在双曲线的左半支上找到一点P,使得 .
. ?(其中
?(其中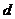 为P到左准线
为P到左准线 的距离)
的距离)
9、如图,已知梯形ABCD中,|AB|=2|CD|,点E在有向线段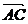 上,且
上,且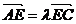 ,双曲线过C、D、E三点,且以A、B为焦点,当
,双曲线过C、D、E三点,且以A、B为焦点,当 时,求双曲线离心率
时,求双曲线离心率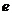 的取值范围.
的取值范围.
班级_______学号__________姓名_________
课后作业
1、如果双曲线 上一点P到右焦点的距离等于
上一点P到右焦点的距离等于 ,那么P到右准线的距离为( )
,那么P到右准线的距离为( )
A.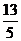 B.13 C.5 D.
B.13 C.5 D.
2、双曲线虚轴的一个端点为M,两焦点为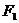 ,
, ,
,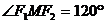 ,则离心率为( )
,则离心率为( )
A.  B.
B.  C.
C. D.
D.
3、设双曲线 两焦点为
两焦点为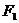 ,
, ,点
,点 为双曲线上除顶点外的任一点,过
为双曲线上除顶点外的任一点,过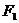 作
作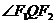 的平分线的垂线,垂足为P,则P的轨迹为( )
的平分线的垂线,垂足为P,则P的轨迹为( )
A.椭圆的一部分 B.双曲线的一部分
C.抛物线的一部分 D.圆的一部分
4、当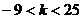 时,双曲线
时,双曲线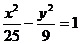 与
与 有相同的( )
有相同的( )
A.渐近线 B.焦点 C.顶点 D.离心率
5、已知双曲线的离心率 ,则它的两条渐近线的夹角为_______________.
,则它的两条渐近线的夹角为_______________.
6、已知椭圆 和双曲线
和双曲线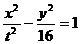 有相同的焦点,则实数
有相同的焦点,则实数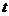 的值是_________.
的值是_________.
7、双曲线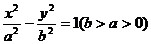 的半焦距为C,直线
的半焦距为C,直线 过
过 ,已知原点到直线
,已知原点到直线 的距离为
的距离为 C,求双曲线的离心率.
C,求双曲线的离心率.
8、双曲线 的右顶点为A,
的右顶点为A, 轴上有一点
轴上有一点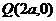 ,若双曲线上存在一点
,若双曲线上存在一点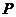 ,使
,使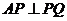 ,求离心率
,求离心率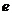 的取值范围.
的取值范围.
9、(选做题)
双曲线 的离心率
的离心率 ,左、右焦点分别为
,左、右焦点分别为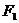 ,
, ,左准线为
,左准线为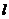 ,能否在双曲线左支上找到一点
,能否在双曲线左支上找到一点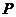 ,使
,使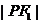 是
是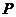 到
到 的距离
的距离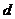 与
与 的等比中项?
的等比中项?
高三数学教学案 第八章 圆锥曲线
第五课时 抛物线
考纲摘录
掌握抛物线的定义,标准方程和抛物线的简单几何性质.
知识概要
抛物线的定义及隐含条件;标准方程的四种形式,四个一(一个顶点,一个焦点,一条准线,一条对称轴)的特征等.
重点、难点
抛物线的性质及应用,抛物线标准方程的求解方法.
基础练习
1、已知抛物线的方程为 ,则它的焦点坐标是____________,准线方程是____________,若该抛物线上一点到
,则它的焦点坐标是____________,准线方程是____________,若该抛物线上一点到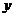 轴的距离等于5,则它到抛物线焦点的距离等于____________,抛物线上的点M到焦点的距离为4,则点M的坐标是____________.
轴的距离等于5,则它到抛物线焦点的距离等于____________,抛物线上的点M到焦点的距离为4,则点M的坐标是____________.
2、抛物线方程为 ,则它的焦点为____________,准线方程为____________.
,则它的焦点为____________,准线方程为____________.
3、动点在原点,关于坐标轴对称,且过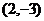 的抛物线方程为____________.
的抛物线方程为____________.
4、斜率为2的直线经过抛物线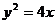 的焦点,与抛物线相交于A、B两点,则|AB|=__________.
的焦点,与抛物线相交于A、B两点,则|AB|=__________.
5、动点M到F(1,0)的距离比到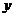 轴的距离大1,则M的轨迹方程为_______________.
轴的距离大1,则M的轨迹方程为_______________.
6、一抛物线拱桥,当拱桥离水面2米时,水面宽4米,则水面下降1米后,水面宽__________米.
例题讲解
例1、抛物线关于 轴对称,顶点是坐标原点,点P(1,2),A(
轴对称,顶点是坐标原点,点P(1,2),A(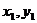 ),B(
),B(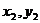 )均在抛物线上;
)均在抛物线上;
(1)写出该抛物线的标准方程及准线方程;
(2)当PA、PB的斜率存在且倾斜角互补时,求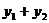 的值及直线AB的斜率.
的值及直线AB的斜率.
例2、(如图),线段AB过 轴正半轴上一定点M(
轴正半轴上一定点M( ),端点A、B到
),端点A、B到 轴距离之积为2m,以
轴距离之积为2m,以 轴为对称轴,过A、O、B三点作抛物线.
轴为对称轴,过A、O、B三点作抛物线.
(1)求抛物线的方程;
(2)若 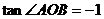 ,求
,求 取值范围.
取值范围.
例3、AB为抛物线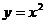 上的动弦,且|AB|=
上的动弦,且|AB|= (
( 为常数,且
为常数,且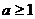 ),求弦AB中点M到
),求弦AB中点M到 轴距离的最小值.
轴距离的最小值.
例4、(选讲题)
AB是过抛物线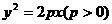 焦点F的弦,M为AB的中点,
焦点F的弦,M为AB的中点,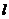 为抛物线的准线,MN⊥
为抛物线的准线,MN⊥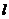 ,N为垂足,求证:
,N为垂足,求证:
(1)AN⊥BN; (2)FN⊥AB;
(3)设MN交抛物线于 ,则
,则 平分MN;
平分MN;
(4)设A(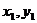 ),B(
),B(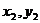 ),则
),则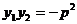 ,
,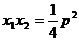 ;
;
(5)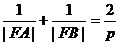 ;
;
(6)过M作ME⊥AB,ME交 轴于E,求证:|EF|=
轴于E,求证:|EF|=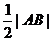 ,
,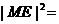 |FA|.|FB|;
|FA|.|FB|;
(7)设BD⊥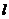 ,D为垂足,则A、O、D三点共线.
,D为垂足,则A、O、D三点共线.
班级_______学号__________姓名_________
课后作业
1、抛物线 上两点A、B到焦点的距离和是5,则线段AB的中点M到
上两点A、B到焦点的距离和是5,则线段AB的中点M到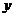 轴的距离是______________.
轴的距离是______________.
2、点A(3,2),F为 的焦点,点M在
的焦点,点M在 上移动,则当|MA|+|MF|取最小值时,M点坐标为__________.
上移动,则当|MA|+|MF|取最小值时,M点坐标为__________.
3、直线AB过 的焦点与其交于A、B两点,O为坐标原点,则
的焦点与其交于A、B两点,O为坐标原点,则 =_________.
=_________.
4、若抛物线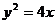 上的点M到直线
上的点M到直线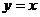 的距离为
的距离为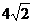 ,则M的坐标为____________.
,则M的坐标为____________.
5、过抛物线焦点F的直线与抛物线相交于A、B两点,若A、B在抛物线准线上的射影分别为A1、B1,则∠A1FB1=______________.
6、直线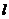 过
过 的焦点,并且与
的焦点,并且与 轴垂直,若
轴垂直,若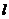 被抛物线截得的弦长为4,则
被抛物线截得的弦长为4,则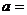 ____________.
____________.
7、已知A、B为抛物线 上对称轴两侧的点,A、B和焦点F的距离分别为6和15,过AB中点M作对称轴的垂线交抛物线于N和N′,求点N、N′到焦点F的距离.
上对称轴两侧的点,A、B和焦点F的距离分别为6和15,过AB中点M作对称轴的垂线交抛物线于N和N′,求点N、N′到焦点F的距离.
8、抛物线顶点在原点,它的准线过双曲线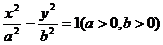 的一个焦点,并与双曲线的实轴垂直,已知抛物线与双曲线的一交点为
的一个焦点,并与双曲线的实轴垂直,已知抛物线与双曲线的一交点为 ,求抛物线与双曲线的方程.
,求抛物线与双曲线的方程.
9、(选做题)
直线 交抛物线
交抛物线 于A、B两点,线段AB的垂直平分线交抛物线的准线于点C.
于A、B两点,线段AB的垂直平分线交抛物线的准线于点C.
(1)求 取值范围;
取值范围;
(2)求点C纵坐标 的取值范围.
的取值范围.