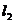1、集合x满足{a,b}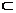 x
x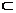 {a,b,c,d,e},则x的个数为( )
{a,b,c,d,e},则x的个数为( )
A 5 B 6 C 7 D 8
2、函数y=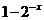 (x∈R)的反函数是( )
(x∈R)的反函数是( )
A y=log2(1-x)(x<1) B
y=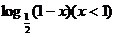
C y=- D y=
D y=
3、已知O为原点,A(a,0),B(0,a),其中a>0,点P在线段AB上,且 (O≤t≤1),则
(O≤t≤1),则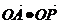 的最大值为(
)
的最大值为(
)
A a B 2a C 3a D a2
4、某种产品有4只次品和6只正品,每只均不同且可以区分,每次取出一只测试,
直到4只次品全部测出为止,则最后一只次品恰好在第五次测试时被发现的不同情况有
A 24 B 144 C 576 D 720
5、直线过P(-3, )且被x2+y2=25截得的弦长为8,则这条直线的方程为( )
)且被x2+y2=25截得的弦长为8,则这条直线的方程为( )
A 3x+4y+15=0 B
x=-3或y= C
x=-3 D x=-3或3x+4y+15=0
C
x=-3 D x=-3或3x+4y+15=0
6、在下列各区间中,函数y=sin2( )的单调减区间是(
)
)的单调减区间是(
)
A  B
B
 C
C
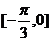 D
D

7、函数f(x)=x3+bx2+cx+d在区间[-1,2]是减函数,那么b+c有( )
A 最大值 B 最大值-
B 最大值- C 最小值
C 最小值 D 最小值-
D 最小值-
8、设(a-b)n的展开式中,二项式系数之和为256,则此二项式展开式中系数最小
的项是( )
A 第5项 B 第4、5项 C 第5、6项 D 第4、6项
9、若方程(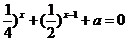 有正数解,则a的取值范围是( )
有正数解,则a的取值范围是( )
A (-∞,1) B (-∞,-2)
C (-3,0) D (log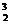 ,+∞)
,+∞)
10、用一个平面去截正三棱锥及其外接球,所得的截面如图所示O为球心,若球
的半径为R,则三棱锥的侧面积为( )
 A
A 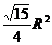 B
B
 C
C 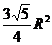 D
D 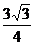 R2
R2
11、不等式组 所表示的平面区域的面积为( )
所表示的平面区域的面积为( )
A 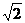 B
B
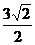 C
C
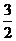 D
2
D
2
12、若钝角三角形的三个内角的度数成等差数列,最大边的长与最小边的长之比值为m,则m的范围是( )
A (1,2) B (2,+∞) C (3,+∞) D [3,+∞)
13、定义在R上的函数f(x)满足f(x+y)=f(x)+f(y),则f(x)一定为_____(填奇、偶函数)。
14、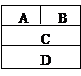 已知(
已知( 9的展开式中x3的系数为
9的展开式中x3的系数为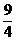 ,则常数a的值为___________。
,则常数a的值为___________。
15、用4种不同的颜色涂入图中的矩形A,B,C,D中,要求相邻的
矩形涂色不同,则不同的涂色方法共有________种。(用数字作答)
16、 如图,F1、F2分别为椭圆
如图,F1、F2分别为椭圆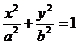 的左、右
的左、右
焦点,P在椭圆上,△OPF2是面积为 的正三角形,
的正三角形,
则b2的值为_____________。
17、函数y=loga(x+ 的值域为R,则a的取值范围是__________。
的值域为R,则a的取值范围是__________。
18、有下列命题:(1)有两个对角面为矩形的棱柱为直棱柱;(2)三个侧面为全等的等腰三角形的棱锥为正三棱锥;(3)四个侧面为全等的矩形的四棱柱为正四棱柱;(4)二面角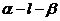 与M-
与M-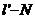 中,若
中,若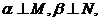 则两二面角相等或互补,其中错误命题的序号为______________。(把你认为错误命题的序号全写上)
则两二面角相等或互补,其中错误命题的序号为______________。(把你认为错误命题的序号全写上)
高三数学综合练习二
班级__________ 姓名____________ 学号_______
13、___________ 14、__________ 15、___________
16、___________ 17、__________ 18、___________
19、已知锐角△ABC中,三个内角为A、B、C,两个向量 =(2-2sinA, cosA+sinA),
=(2-2sinA, cosA+sinA),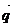 =(sinA-cosA,1+sinA),若
=(sinA-cosA,1+sinA),若 与
与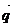 是共线向量。
是共线向量。
(1)求∠A的大小;
(2)函数y=2sin2B+cos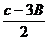 取最大值时,求∠B的大小。
取最大值时,求∠B的大小。
20、 从边长为2a的正方形铁片四个角各截去一个边长为x的正方形,然后折成一个无盖的长方体的盒子,要求长方体的高度x与底面正方形的边长的比不超过正常数m(如图所示).
从边长为2a的正方形铁片四个角各截去一个边长为x的正方形,然后折成一个无盖的长方体的盒子,要求长方体的高度x与底面正方形的边长的比不超过正常数m(如图所示).
(1)把铁盒的体积V表示为x的函数,并指出其定义域;
(2)x为何值时,容量V有最大值。

21、 如图所示的多面体是由底面为ABCD的直平行六面体被截面AEFG所截而成的,其中底面ABCD为菱形,∠BAD=600,AB=4,BE=2,CF=3。
如图所示的多面体是由底面为ABCD的直平行六面体被截面AEFG所截而成的,其中底面ABCD为菱形,∠BAD=600,AB=4,BE=2,CF=3。
(1)求异面直线EF与AD所成角的正切值;
(2)求截面AEFG与底面ABCD所成二面角的正切值;
(3)求点C到面AEFG的距离。
22、数列{an}中,Sn为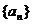 的前n项和,an为Sn与2的等差中项,数列{bn}中,b1=1,点P(bn,bn+1)在直线x-y+2=0上。
的前n项和,an为Sn与2的等差中项,数列{bn}中,b1=1,点P(bn,bn+1)在直线x-y+2=0上。
(1)求{an},{bn}的通项公式;
(2){bn}的前n项和为Bn,试比较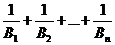 与2的大小,并说明理由;
与2的大小,并说明理由;
(3)设Tn= ,若Tn<C,(C∈Z),求C的最小值。
,若Tn<C,(C∈Z),求C的最小值。
23、如图,双曲线 的两条渐近线为
的两条渐近线为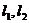 ,右焦点为F,斜率为K且过F的直线
,右焦点为F,斜率为K且过F的直线 分别交
分别交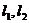 ,双曲线的右支于A、B、C三点;
,双曲线的右支于A、B、C三点;
(1)若 ,试用k表示
,试用k表示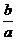 ;
;
(2)若B、C三等分AF,求双曲线的离心率e;
(3)若C是BF的中点,当k∈(-1,0)时,求双曲线离心率e的取值范围。