
1.设全集U={-2,-1,0,1,2},A={-2,-1,0},B={0,1,2},则(CUA)∩B= ( )
A.{0} B.{-2,-1} C.{1,2} D.{0,1,2}
2.“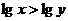 ”是“
”是“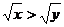 ”的
( )
”的
( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
3. 一组数据中的每一个数据都减去80,得到一组新数据,若这组新数据的平均数是1.2,
方差是4.4,则原来一组数据的平均数和方差分别是 ( )
A.81.2,4.4 B.78.8,4.4 C.81.2,84.4 D.78.8,75.6
4 下列函数中, 在区间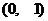 上为减函数的是 ( )
上为减函数的是 ( )
A. 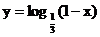 B.
B.
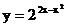
C. 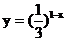 D.
D.
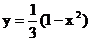
5.已知数列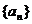 满足
满足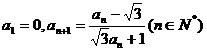 ,则
,则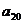 = ( )
= ( )
A.0 B.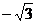 C.
C.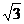 D.
D.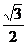
6.已知点O(0,0),A(a,0),B(0,a)其中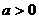 ,
,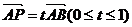 ,则
,则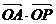 的最大值 A.
的最大值 A.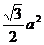 B.
B.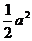 C.
C.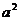 D.
D.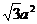 (
)
(
)
7.已知双曲线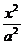 -
-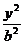 =1(a>0,b>0)的右焦点为F,右准线与一条渐近线交于点A,△OAF的面积为
=1(a>0,b>0)的右焦点为F,右准线与一条渐近线交于点A,△OAF的面积为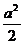 (O为原点),则两条渐近线的夹角为 ( )
(O为原点),则两条渐近线的夹角为 ( )
A.30º B.45º C.60º D.90º
|
8 |
1 |
6 |
|
3 |
5 |
7 |
|
4 |
9 |
2 |
8.把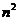 个正整数
个正整数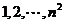 填入
填入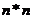 方格中,使得
方格中,使得
每行,每列,每条对角线上的数的和相等,这个正方形
叫n阶幻方,记f(n)为对角线上数的和,如图就是一
个3阶幻方,可知f(3)=15.则f(4)= ( )
A 32 B 33 C 34 D 35
9.函数f(x)=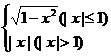 ,如果方程f(x)=a有且只有一个实根,那么a满足( )
,如果方程f(x)=a有且只有一个实根,那么a满足( )
A.a<0 B.0≤a<1 C.a=1 D.a>1
10. 设函数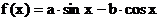 图象的一条对称轴方程为
图象的一条对称轴方程为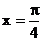 , 则直线
, 则直线
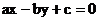 的倾斜角为
( )
的倾斜角为
( )
A. 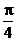 B.
B.
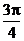 C.
C.  D.
D.
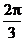
11.如果数列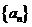 的通项公式为
的通项公式为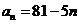 ,
,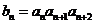 ,则数列
,则数列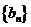 的前
的前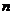 项和
项和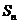 中最大的是
( )
中最大的是
( )
(A>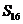 (B)
(B)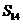 (C>
(C>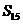 (D)
不确定
(D)
不确定
12.函数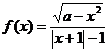 为奇函数的充要条件是
(
)
为奇函数的充要条件是
(
)
A、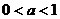 B、
B、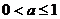 C、
C、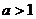 D、
D、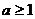
13.设直线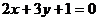 和圆
和圆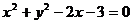 相交于点A、B,则弦AB的垂直平分线方程是
.
相交于点A、B,则弦AB的垂直平分线方程是
.
14. “渐减数”是指每个数字比其左边数字小的正整数(如98765),若把所有五位渐减数按从小到大的顺序排列,则第55个数为
.
“渐减数”是指每个数字比其左边数字小的正整数(如98765),若把所有五位渐减数按从小到大的顺序排列,则第55个数为
.
15.给出平面区域如图所示, 目标函数为:
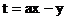
若当且仅当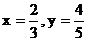 时, 目标函数t取最小值,
时, 目标函数t取最小值,
则实数a的取值范围是 .
16.已知平面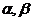 和直线,给出条件:①
和直线,给出条件:①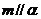 ;②
;②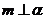 ;③
;③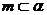 ;④
;④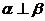 ;⑤
;⑤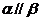 .
.
(i)当满足条件
时,有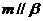 ;(ii)当满足条件
时,有
;(ii)当满足条件
时,有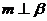 .
.
(填所选条件的序号)
高三数学周练试题(五)
班级_______________ 姓名_________________ 学号________
13、 14、 15、 16、① ②
17.(本小题满分10分)
多向飞碟是奥运竞赛项目,它是由跑靶机把碟靶(射击目标)在一定范围内从不同方向飞出,每抛出一个碟靶,都允许运动员射击两次。一运动员进行多向飞碟训练时,每次射击碟靶的概率为p与运动员离碟靶的距离S(m)成反比,现有一碟靶抛出后离运动员的距离S(m)与飞行时间t(s)满足S=15(t+1),.若运动员在碟靶飞出0.5s时进行第一次射击,命中的概率0.8,若他发现没有命中,则在进行第一次射击后过0.5s进行第二次射击,求他命中此靶的概率。
18.(本小题满分12分)
设向量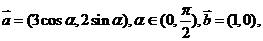
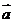 与
与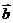 的夹角为
的夹角为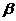
(1)求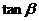 (用
(用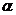 表示)
表示)
(2) 试求 的最大值及对应的
的最大值及对应的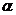 值。
值。
19.(本小题满分12分)
如图,在棱长为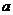 的正方体ABCD-A1B1C1D1中,EF分别为棱AB和BC的中点,EF交BD于H。
的正方体ABCD-A1B1C1D1中,EF分别为棱AB和BC的中点,EF交BD于H。
(1)求二面角B1-EF-D的正切值;(2)设M为BB1中点,求证D1M⊥平面EFB1;
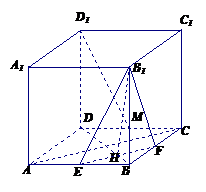 (3)求点D到平面EFB1的距离。
(3)求点D到平面EFB1的距离。
20(本小题满分12分)
已知函数 , 且
, 且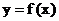
的图象经过点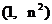 , 数列
, 数列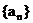 为等差数列.
为等差数列.
(1) 求数列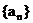 的通项公式
的通项公式
(2) 当n为奇数时, 设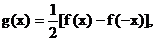 试求
试求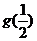
21.(本小题满分14分)
如图,曲线C是顶点在原点,以x轴为对称轴开口向右的抛物线,点M(2,1)到抛物线准线的距离为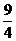 。
。
 (1)求抛物线C的方程;
(1)求抛物线C的方程;
(2)若直线l过抛物线上P、Q不同两点,且与x轴
交于点T,与y轴交于点S,求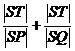 的取值范围;
的取值范围;
(3)若过点M的直线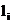 (i=1,2,3,4)分别与抛物线
(i=1,2,3,4)分别与抛物线
C交于上下两点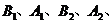
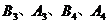 ,
,
又点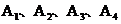 的纵坐标依次成公差不为零的等差数列,
的纵坐标依次成公差不为零的等差数列,
试分析推导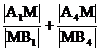 与
与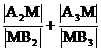 的大小.
的大小.
22.(本小题满分14分)
设函数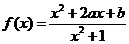 ,其中
,其中 ,
,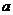 、
、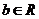 .
.
(Ⅰ)若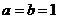 ,求函数
,求函数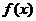 的值域;
的值域;
(Ⅱ)存在实数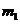 、
、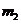 (
(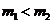 )满足等式
)满足等式 ,(
,(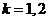 );
);
(Ⅲ)对于(Ⅱ)中的实数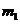 、
、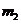 ,有
,有 成立.
成立.