
1、设A、B是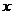 轴上的两点,点P的横坐标为2,且|PA|=|PB|,若直线PA的方程为
轴上的两点,点P的横坐标为2,且|PA|=|PB|,若直线PA的方程为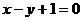 ,则直线PB的方程是( )
,则直线PB的方程是( )
A.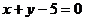 B.
B.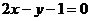 C.
C.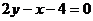 D.
D.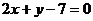
2、三条直线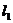 :
: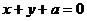 ,
, :
: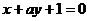 ,
,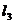 :
: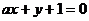 能构成三角形的条件是( )
能构成三角形的条件是( )
A.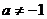 B.
B.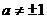 C.
C.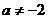 D.以上均不对
D.以上均不对
3、圆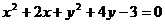 到直线
到直线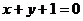 的距离为
的距离为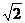 的点共有 ( )
的点共有 ( )
A.1个 B.2个 C.3个 D.4个
4、方程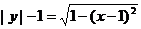 表示的曲线是 ( )
表示的曲线是 ( )
A.抛物线 B.一个圆 C.两个圆 D.两个半圆
5、平面直角坐标系中,O是坐标原点,已知两点A(3,1),B(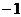 ,3),若点C满足
,3),若点C满足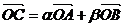 ,其中
,其中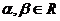 ,且
,且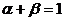 ,则点C的轨迹方程是( )
,则点C的轨迹方程是( )
A.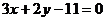 B.
B.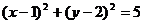
C.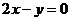 D.
D.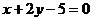
6、函数 的图象与
的图象与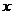 轴、
轴、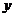 轴有三个不同的交点,有一个圆恰经过这三点,则此圆与坐标轴的另一个交点的坐标是( )
轴有三个不同的交点,有一个圆恰经过这三点,则此圆与坐标轴的另一个交点的坐标是( )
A.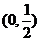 B.(0,1) C.
B.(0,1) C.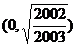 D.
D.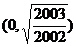
7、直线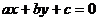 的某一侧点
的某一侧点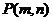 满足
满足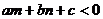 ,则当
,则当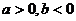 时该点
时该点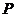 位于该直线的( )
位于该直线的( )
A.右上方 B.右下方 C.左上方 D.左下方
8、与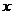 轴,
轴,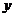 轴都相切的圆的圆心为P点,且圆P过坐标为(1,8)的点,到P点的坐标为 ( )
轴都相切的圆的圆心为P点,且圆P过坐标为(1,8)的点,到P点的坐标为 ( )
A.(5,5) B.(13,13) C.(5,5)及(13,13) D.不确定
9、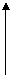 直线
直线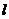 过点
过点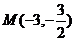 且被圆
且被圆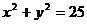 截得的弦长为8,则
截得的弦长为8,则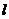 方程是____________.
方程是____________.
10、函数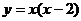 在[
在[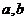 ](
](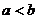 )上的值域是
)上的值域是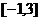 ,
,
则以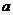 为横坐标,
为横坐标,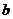 为纵坐标所成的点(
为纵坐标所成的点(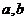 )的轨迹是图
)的轨迹是图
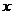
 中的_______________.
中的_______________.
11、已知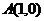 ,
,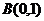 ,
,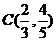 ,目标函数
,目标函数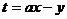 的可行域为四边形OACB,若
的可行域为四边形OACB,若
当且仅当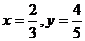 时,目标函数
时,目标函数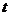 取最小值,则实数
取最小值,则实数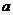 的取值范围是_____________.
的取值范围是_____________.
12、已知点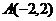 ,
,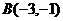 ,试在直线
,试在直线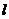 :
: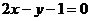 上找一点P,使|PA|+|PB|最小,则点P坐标为_____________.
上找一点P,使|PA|+|PB|最小,则点P坐标为_____________.
13、已知直线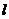 :
: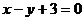 ,圆C:
,圆C: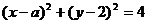
(1)求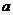 的值,使
的值,使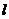 被C截得的弦最长;
被C截得的弦最长;
(2)求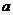 的值,使直线
的值,使直线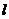 与
与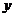 轴交点将弦分为1:2线段.
轴交点将弦分为1:2线段.
|
|
甲 |
乙 |
丙 |
利润(万元/吨) |
|
A产品 |
4 |
9 |
3 |
7 |
|
B产品 |
5 |
4 |
10 |
12 |
14、某厂生产A、B两产品,需甲、乙、丙三种原料,每生产一吨产品需耗原料如下表,现有甲原料200吨,乙原料360吨,丙原料300吨,若产品生产后能全部销售,试问A、B各生产多少吨能获最大利润.
15、随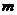 的变化,方程
的变化,方程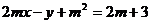 表示无数条直线,对于某点P在且只在这些直线中的某一条上,将所有这样的点P组成集合M.
表示无数条直线,对于某点P在且只在这些直线中的某一条上,将所有这样的点P组成集合M.
(1)判断点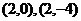 是否属于M,简述理由;
是否属于M,简述理由;
(2)求点P的轨迹C的方程;
(3)若曲线C与它关于点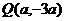 对称的曲线C1有两个不同的交点A、B,求直线AB斜率的取值范围.
对称的曲线C1有两个不同的交点A、B,求直线AB斜率的取值范围.