
1.设M={(x,y)|(x-2)2+y2=4},N={(x,y)|(x-1)2+y2=1},则下列结论中正确的是 ( )
A. M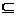 N
B. M∩N= Φ C. N
N
B. M∩N= Φ C. N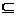 M
D. M∩N={(0,0)}
M
D. M∩N={(0,0)}
2.函数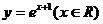 的反函数是 ( )
的反函数是 ( )
A. B.
B.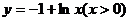
C.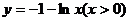 D.
D.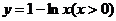
3.若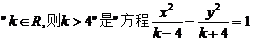 表示双曲线”的 ( )
表示双曲线”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.即不充分也不必要条件
4.某单位邀请10位教师中的6位参加一个会议,其中甲、乙两位教师不能同时参加,则邀请的不同方法有 ( )
A.84种 B.98种 C.112种 D.140种
5.设正数x,y满足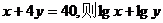 的最大值是 ( )
的最大值是 ( )
A.1 B.2 C.4 D.10
6.把直线 平移后,所得直线与圆
平移后,所得直线与圆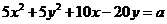
相切,则则实数a的值为 ( )
A.-39 B.-21 C.13 D.39
7.若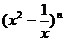 的展开式中含x的项为第6项,设
的展开式中含x的项为第6项,设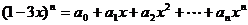 则
则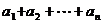 的值为 ( )
的值为 ( )
A.-225 B.-32 C.32 D.255
8.若不等式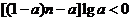 对于任意正整数
对于任意正整数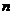 恒成立,则实数
恒成立,则实数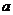 的取值范围是(
)
的取值范围是(
)
A.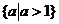 B.
B.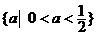
C. D.
D.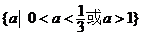
第Ⅱ卷(非选择题,共110分)
9.曲线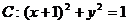 关于直线y=1对称的曲线方程是 .
关于直线y=1对称的曲线方程是 .
10.在一批产品中,有n件一级品,36件二级品,60件三级品,现按分层抽样的方法抽出的20件样品中,有10件三级品,则n= .
11.已知 =
.
=
.
12.实数 ,
, 满足不等式组
满足不等式组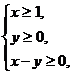 则
则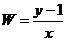 的取值范围是
.
的取值范围是
.
13.以椭圆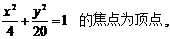 一条渐近线为y=2x的双曲线的方程
.
一条渐近线为y=2x的双曲线的方程
.
14.球面上有三个点A、B、C组成球的一个内接三角形,若AB=6,BC=8,AC=10,且球心到△ABC所在平面的距离等于球半径的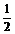 ,那么这个球面面积是 .
,那么这个球面面积是 .
15.(本题满分13分)已知A、B、C为 的三个内角,
的三个内角,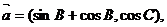

(Ⅰ)若 求角A;
求角A;
(Ⅱ)若 ,求tan2A.
,求tan2A.
16.(本小题满分13分)已知函数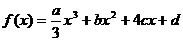 的图象关原点对称,
的图象关原点对称,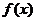 的图象在点P(1,m)处的切线的斜率为-6,且当x=2时
的图象在点P(1,m)处的切线的斜率为-6,且当x=2时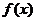 有极值.
有极值.
(Ⅰ)求a,b,c,d的值
(Ⅱ)若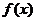 在区间
在区间 上是增函数,求n的取值范围.
上是增函数,求n的取值范围.
17.(本小题满分14分)在一次抗洪抢险中,准备用射击的方法引爆从河上游漂流而下的一巨大汽油罐,已知只有5发子弹备用,且首次命中只能使汽油流出,再次命中才能引爆成功,每次射击命中率都是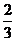 ,每次命中与否互相独立.
,每次命中与否互相独立.
(Ⅰ)直到第三次射击汽油才流出的概率;
(Ⅱ)直到第三次射击油罐才被引爆的概率;
(Ⅲ)求油罐被引爆的概率.
18.(本题满分14分)如图在长方体ABCD-A1B1C1D1中,棱AD=DC=3,DD1=4,E是AA1的中点.
 (1)求证:A1C∥平面BED;
(1)求证:A1C∥平面BED;
(2)求二面角E-BD-A的大小;
(3)求点E到平面A1BCD1的距离.
19.(本题满分14分)数列{an}(n∈N*)中,a1=1,且an+1=2an+1,又设bn=an+1,
(1)求证:数列{bn}是等比数列;
(2)求数列{an}的通项公式;
(3)设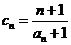 (n∈N*),求数列{cn}的前n项和Sn.
(n∈N*),求数列{cn}的前n项和Sn.
20. (本题满分14分)椭圆C: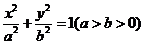 的两个焦点为F1,F2,点P在椭圆C上,且
的两个焦点为F1,F2,点P在椭圆C上,且
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l过圆x2+y2+4x-2y=0的圆心,交椭圆C于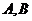 两点,且A、B关于点M对称,求直线l的方程.
两点,且A、B关于点M对称,求直线l的方程.
高考模拟测试数学(文科) 第Ⅰ卷(选择题,共40分)参考答案
高考模拟测试数学(文科)参考答案
一、选择题:(本题共10个小题,每小题5分,共50分。)
DBAD ADDC
二、填空题:本大题共6小题,每小题4分,共24分
9.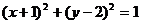 10.24 11.2 12.
10.24 11.2 12.
13. 14.
14.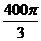
三、解答题:本大题共6小题,共74分
15.解:
(Ⅰ)由已知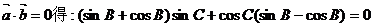
化简得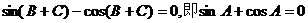 (3分)
(3分)

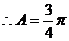 (5分)
(5分)
(Ⅱ)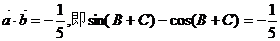
 ①,平方得
①,平方得

 ②(7分)
②(7分)
联立①、②得,
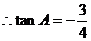 (10分)
(10分)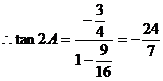 (12分)
(12分)
16.解:
(Ⅰ) ………………2分
………………2分
由条件可得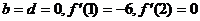 ………………4分
………………4分
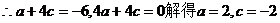
故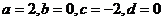 ………………6分
………………6分
(Ⅱ)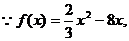
 ………………8分
………………8分
令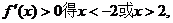
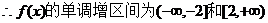 ;………………10分
;………………10分
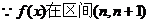 上是增函数
上是增函数
 即
即 …12分
…12分
17.解:
(Ⅰ)第三次射击汽油才流出的概率
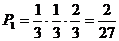 ………………3分
………………3分
(Ⅱ)第三次射击被引爆的概率
 ………………7分
………………7分
(Ⅲ)“油罐被引的事件为事件A,其对立事件为 ”则
”则
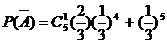
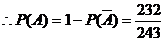 ………………12分
………………12分
18.(本小题满分14分)
解法一:
|
有A1C∥EO.
∵EO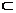 平面BED,A1C
平面BED,A1C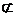 平面BED,
平面BED,
∴A1C∥平面BED.
(II)∵AC⊥BD于O,
又∵E是AA的中点,∴EB=ED.
∴EO⊥BD.
∴∠EOA是二面角E-BD-A的平面角.
在Rt△EAO中,EA=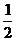 AA1=2,AO=
AA1=2,AO=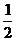 AC=
AC=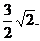
∴tAnEOA=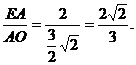
二面角E-BD-A的大小是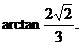 …………………………………9分
…………………………………9分
(III)过点E作EF⊥A1B于F.
∵A1D1⊥平面A1B1BA,EF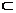 平面A1B1BA,
平面A1B1BA,
∴A1D1⊥EF且A1B∩A1D1=A1.
∴EF⊥平面A1BCD1.…………………………………………………………11分
则EF的长是点E到平面A1BCD1的距离.…………………………………12分
∵ 且A1E=2,A1B=5,AB=3,
且A1E=2,A1B=5,AB=3,
∴EF=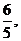 即点E到平面A1BCD1的距离是
即点E到平面A1BCD1的距离是 …………………………14分
…………………………14分
解法二:
(I)如图建立空间直角坐标系,取BD的中点O,
|
A1(0,0,4),C(3,3,0),
E(0,0,2),O(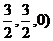 …………2分
…………2分
 ,
,
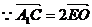 ,∴A1C∥EO.
,∴A1C∥EO.
∵EO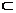 平面BED,A1C
平面BED,A1C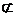 平面BED,
平面BED,
∴A1C∥平面BED.…………………………5分
(II)由于AE⊥平面ABCD,则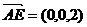 就是平面ABCD的法向量.…………6分
就是平面ABCD的法向量.…………6分
B(3,0,0),D(0,3,0),
设平面EBD的法向量为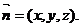
由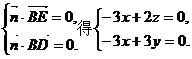
令z=3,则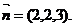 ……………………………………………………7分
……………………………………………………7分

∴二面角E-BD-A的大小为arrccos  .………………………………9分
.………………………………9分
(III)D1(0,3,4),则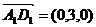 ,设平面A1BCD1的法向量为
,设平面A1BCD1的法向量为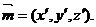
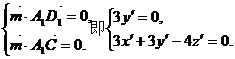
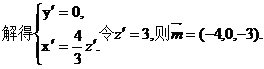
即点E到平面A1BCD1的距离是
又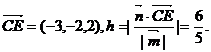 …………………………………………14分
…………………………………………14分
(20)(共14分)
解法一:
(Ⅰ)因为点P在椭圆C上,所以 ,a=3.
,a=3.
在Rt△PF1F2中,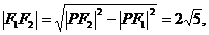 故椭圆的半焦距c=
故椭圆的半焦距c=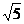 ,
,
从而b2=a2-c2=4, 所以椭圆C的方程为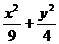 =1.
=1.
(Ⅱ)设A,B的坐标分别为(x1,y1)、(x2,y2).
已知圆的方程为(x+2)2+(y-1)2=5,所以圆心M的坐标为(-2,1).
从而可设直线l的方程为 y=k(x+2)+1,
代入椭圆C的方程得 (4+9k2)x2+(36k2+18k)x+36k2+36k-27=0.
因为A,B关于点M对称.
所以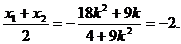 解得
解得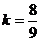 ,
,
所以直线l的方程为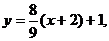 即8x-9y+25=0.
即8x-9y+25=0.
(经检验,所求直线方程符合题意)
解法二:
(Ⅰ)同解法一.
(Ⅱ)已知圆的方程为(x+2)2+(y-1)2=5,所以圆心M的坐标为(-2,1).
设A,B的坐标分别为(x1,y1),(x2,y2).由题意x1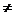 x2且
x2且
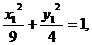 ①
①
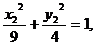 ②
②
由①-②得
 ③
③
因为A、B关于点M对称,所以x1+ x2=-4, y1+ y2=2,
代入③得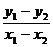 =
=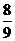 ,即直线l的斜率为
,即直线l的斜率为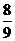 ,
,
所以直线l的方程为y-1=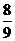 (x+2),即8x-9y+25=0.
(x+2),即8x-9y+25=0.
(经检验,所求直线方程符合题意.)