
1.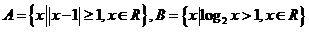 ,则“
,则“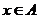 ”是“
”是“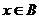 ”的
( )
”的
( )
(A)充分非必要条件 (B)必要非充分条件
(C)充分必要条件 (D)既非充分也非必要条件
2.计算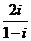 得
( )
得
( )
(A)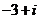 (B)
(B)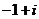 (C)
(C)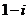 (D)
(D)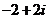
3.设m,n是两条不同的直线,α、β、γ是三个不同的平面。给出下列四个命题:
①若m⊥α,n∥α,则m⊥n; ②若α⊥γ,β⊥γ,则α∥β;
③若m∥α,n∥α,则m∥n; ④若α∥β,β∥γ,m⊥α,,则m⊥γ.
其中正确命题的序号是: ( )
(A) ①和② (B)②和③ (C)③和④ (D)①和④
4.若把一个函数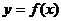 的图象按a
的图象按a 平移后得到函数
平移后得到函数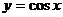 的图象,则函数
的图象,则函数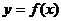 的解析式为 ( )
的解析式为 ( )
A.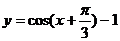 B.
B.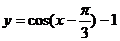
C.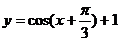 D.
D.
5.已知以椭圆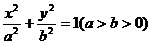 的右焦点F为圆心,a为半径的圆与椭圆的右准线交于不同的两点,则该椭圆的离心率的取值范围是 ( )
的右焦点F为圆心,a为半径的圆与椭圆的右准线交于不同的两点,则该椭圆的离心率的取值范围是 ( )
A.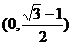 B.
B.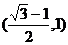 C.
C.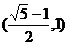 D.
D.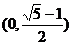
6.8名运动员参加男子100米的决赛. 已知运动场有从内到外编号依次为1,2,3,4,5,6,7,8的八条跑道,若指定的3名运动员所在的跑道编号必须是三个连续数字(如:4,5,6),则参加比赛的这8名运动员安排跑道的方式共有 ( )A.360种 B.4320种 C.720种 D.2160种
7.定点N(1,0),动点A、B分别在图中抛物线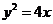 及椭圆
及椭圆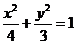 的实线部分上运动,
的实线部分上运动,
且AB∥x轴,则△NAB的周长l取值范围是( )
 (A)(
(A)(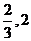 ) (B)(
) (B)(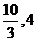 )(C)(
)(C)(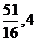 ) (D)(
) (D)(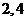 )
)
8.设地球的半径为R,若甲地位于北纬35°东经110°,
乙地位于南纬85°东经110°,则甲、乙两地的球
面距离为 ( )
A.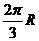 B.
B.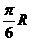
C.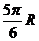 D.
D.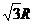
9.已知函数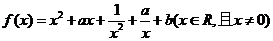 .若实数
.若实数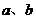 使得
使得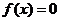 有实根,则
有实根,则
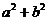 的最小值为
( )
的最小值为
( )
(A)  (B)
(B)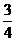 (C) 1 (D)2
(C) 1 (D)2
10.已知m>n>0,则当m2 + 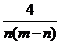 取最小值时,m + n 的值是
( )
取最小值时,m + n 的值是
( )
A.2 B.3 C.4 D.5
11.已知函数① ;②
;②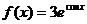 ;③
;③ ;④
;④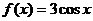 .其中对于
.其中对于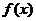
定义域内的任意一个自变量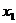 都存在唯一个个自变量
都存在唯一个个自变量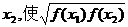 =3成立的函数是
=3成立的函数是
( )
A.①②④ B.②③ C.③ D.④
12.我们可以用以下方法来求方程 的近似根:设
的近似根:设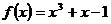 ,由
,由 ,
, ,可知方程必有一根在区间
,可知方程必有一根在区间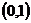 内;再由
内;再由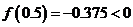 ,可知方程必有一根在区间
,可知方程必有一根在区间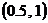 内;依此类推,此方程必有一根所在的区间是
(
)
内;依此类推,此方程必有一根所在的区间是
(
)
A 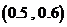 B
B
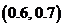 C
C
 D
D
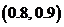
13.过点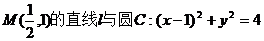 交于A、B两点,C为圆心,当∠ACB最小时,直线l的方程为
.
交于A、B两点,C为圆心,当∠ACB最小时,直线l的方程为
.
14.四面体 中,
中,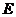 是
是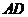 中点,
中点,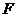 是
是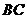 中点,
中点,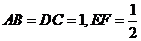 ,则直线
,则直线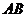 与
与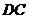 所成的角大小为
所成的角大小为
15.已知定义在正实数集上的连续函数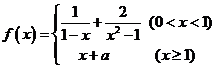 ,则实数
,则实数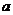 的值为 .
的值为 .
16.某资料室在计算机使用中,如右表所示,编码以一定规则排列,且从左至右以及从上到下都是无限的. 此表中,主对角线上数列1,2,5,10,17,…的通项公式为 ;编码100共出现 次.
|
1 |
1 |
1 |
1 |
1 |
1 |
… |
|
1 |
2 |
3 |
4 |
5 |
6 |
… |
|
1 |
3 |
5 |
7 |
9 |
11 |
… |
|
1 |
4 |
7 |
10 |
13 |
16 |
… |
|
1 |
5 |
9 |
13 |
17 |
21 |
… |
|
1 |
6 |
11 |
16 |
21 |
26 |
… |
|
… |
… |
… |
… |
… |
… |
… |
(共74分)
17.(本小题满分12分)
已知函数
(I)求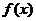 的最小正周期;
的最小正周期;
(II)求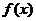 函数图象的对称轴方程;
函数图象的对称轴方程;
(III)求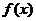 的单调区间.
的单调区间.
18.(本小题满分12分)
某中学排球队进行发球训练,每人在一轮练习中最多可发球4次,且规定一旦发球成功即停止
该轮练习,否则一直发到4次为止. 已知队员甲发球成功的概率为0.6.
|
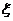 的分布列,并求出
的分布列,并求出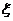 的数学期望E
的数学期望E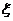 ;
;
(II)求一轮练习中队员甲至少发球3次的概率.
19. (本小题12分)
(本小题12分)
四棱锥P-ABCD中,PA⊥底面ABCD,AB // CD,
AD=CD=1,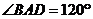 ,
,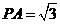 ,
,
 .
.
(I)求证: 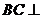 平面
平面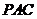 ;
;
(Ⅱ)求二面角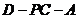 的大小;
的大小;
(Ⅲ)求点 到平面
到平面 的距离.
的距离.
20.(本小题12分)
已知函数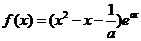 (
(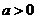 且).
且).
(Ⅰ) 当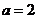 时,求函数
时,求函数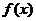 的单调区间;
的单调区间;
(Ⅱ) 若不等式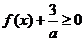 对
对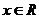 恒成立,求a的取值范围.
恒成立,求a的取值范围.
21.(本小题满分12分)
已知平面上两定点M(0,-2)、N(0,2),P为一动点,满足 .
.
(I)求动点P的轨迹C的方程;
(II)若A、B是轨迹C上的两不同动点,且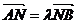 . 分别以A、B为切点作轨迹C的切线,设其交点Q,证明
. 分别以A、B为切点作轨迹C的切线,设其交点Q,证明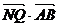 为定值.
为定值.
22.(本小满分14分)
已知函数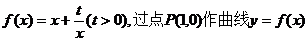 的两条切线PM、PN,切点分别为
的两条切线PM、PN,切点分别为
M、N.
(I)当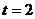 时,求函数
时,求函数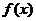 的单调递均区间;
的单调递均区间;
(II)设|MN|= ,试求函数
,试求函数 的表达式;
的表达式;
(III)在(II)的条件下,若对任意的正整数 ,在区间
,在区间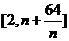 内总存在
内总存在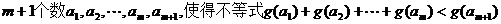 成立,求m的最大值.
成立,求m的最大值.
高考理科数学试题Ⅰ参考答案
2007年4月彭泽二中理科数学试题Ⅰ参考答案
一、选择题
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
B |
B |
D |
D |
C |
B |
B |
A |
A |
B |
C |
B |
二、填空题
13.
14.
15. 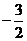
16.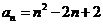 (n∈N+); 6
(n∈N+); 6
17.(本小题满分12分)
解:

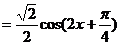
(I)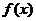 的最小正周期
的最小正周期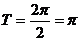 .
.
(II)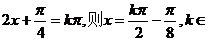 Z.
Z.
∴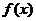 函数图象的对称轴方程是
函数图象的对称轴方程是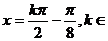 Z.
Z.
(注:若写成 )
)
(III)
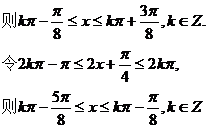
故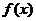 的单调区间为
的单调区间为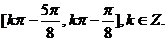
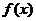 的单调减区间为
的单调减区间为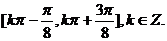
18.(本小题满分12分)
解:(I)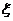 的可能取值为1,2,3,4.
的可能取值为1,2,3,4.
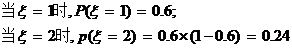

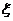 |
1 |
2 |
3 |
4 |
|
P |
0.6 |
0.24 |
0.096 |
0.064 |
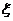 的数学期望为
的数学期望为
 .
.
(II)在一轮练习中队员甲至少发球3次的概率为
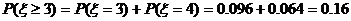
19(本小题12分)解法一:
(1)
证明: PA⊥底面ABCD,
PA⊥底面ABCD,
 平面ABCD,
平面ABCD, ,
,
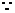 ∠
∠ =
=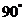 ,
,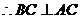 .
.
又 ,
,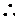
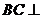 平面
平面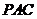 .
.
(2) 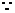 AB // CD,
AB // CD, 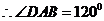
.∠ADC=600,又AD =CD=1,
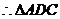 为等边三角形,且 AC=1.
为等边三角形,且 AC=1.
取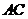 的中点
的中点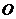 ,则
,则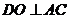 ,
,
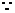 PA⊥底面ABCD,
PA⊥底面ABCD,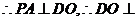 平面
平面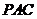
过 作
作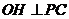 ,垂足为
,垂足为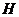 ,连
,连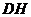 ,由三垂线定理知
,由三垂线定理知 .
.
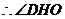 为二面角
为二面角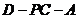 的平面角.由
的平面角.由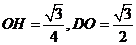 .
.
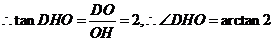 .
.
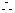 二面角
二面角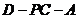 的大小为
的大小为 .
.
(3)设点 到平面
到平面 的距离的距离为
的距离的距离为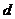 .
.
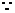 AB // CD,
AB // CD, 平面
平面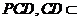 平面
平面 ,
, 平面
平面 .
.
∴点 到平面
到平面 的距离等于点
的距离等于点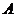 到平面
到平面 的距离.
的距离.
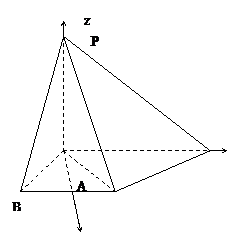
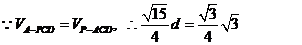
,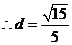 .
.
解法二
(1) 同解法一;
(2) 取 的中点
的中点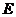 ,则
,则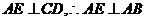 .
.
又PA⊥底面ABCD,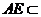 面
面 ,
,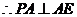
建立空间直角坐标系,如图.则
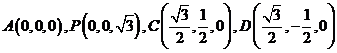 ,
,
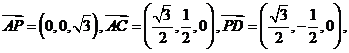
7分
设 为平面
为平面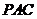 的一个法向量,
的一个法向量,
 为平面
为平面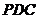 的一个法向量,则
的一个法向量,则
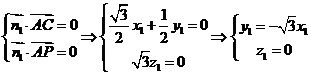 ,可取
,可取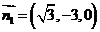 ;
;
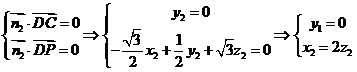 ,可取
,可取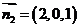 .
.
 .
.
故所求二面角的大小为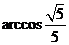 .
.
(3) 又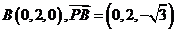 .
.
由(Ⅱ)取平面 的一个法向量
的一个法向量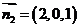 ,
,
 点
点 到平面
到平面 的距离的距离为
的距离的距离为
. 
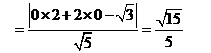
20.(本小题12分)
解: 对函数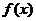 求导得:
求导得: ……………
……………
(Ⅰ)当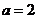 时,
时, 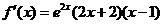
令 解得
解得
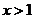 或
或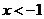
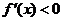 解得
解得
所以, 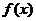 单调增区间为
单调增区间为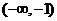 ,
,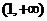 ,
,
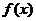 单调减区间为(-1,1)
单调减区间为(-1,1)
(Ⅱ) 令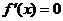 ,即
,即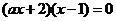 ,解得
,解得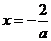 或
或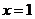
由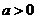 时,列表得:
时,列表得:
|
x |
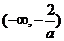 |
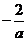 |
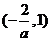 |
1 |
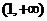 |
 |
+ |
0 |
- |
0 |
+ |
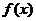 |
 |
极大值 |
 |
极小值 |
 |
对于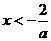 时,因为
时,因为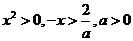 ,所以
,所以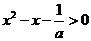 ,
,
∴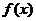 >0
10 分
>0
10 分
对于 时,由表可知函数在
时,由表可知函数在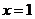 时取得最小值
时取得最小值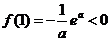
所以,当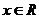 时,
时,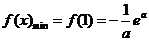
由题意,不等式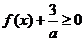 对
对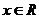 恒成立,
恒成立,
所以得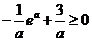 ,解得
,解得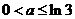
21.(本小题满分12分)
解:(I)设
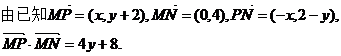
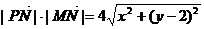

即动点P的轨迹C为抛物线,其方程为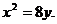
(II)解法一:由已知N(0,2).
|
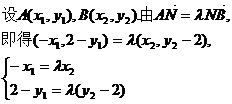
将(1)式两边平方并把
解(2)、(3)式得 ,
,
且有
抛物线方程为
所以过抛物线上A、B两点的切线方程分别是



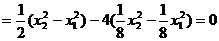
所以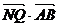 为定值,其值为0.
为定值,其值为0.
解法二:由已知N(0,2)
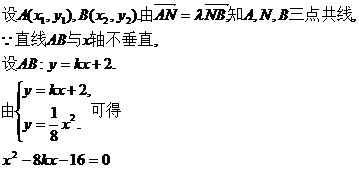

以下同解法一
22.(本小题满分14分)
解:(I)当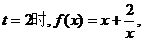
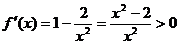
 .
.
则函数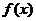 有单调递增区间为
有单调递增区间为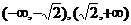
(II)设M、N两点的坐标分别为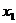 、
、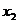 ,
,
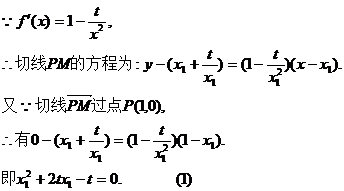
同理,由切线PN也过点(1,0),得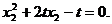 (2)
(2)
由(1)、(2),可得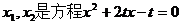 的两根,
的两根,
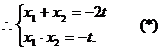

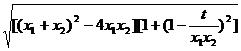
把(*)式代入,得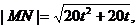
因此,函数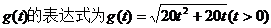 …………9分
…………9分
(III)易知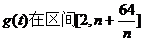 上为增函数,
上为增函数,
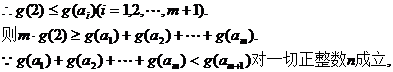
 ……11分
……11分
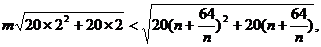

由于m为正整数, .
.
又当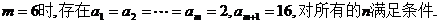
因此,m的最大值为6.