
1.已知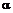 是第三象限的角,则
是第三象限的角,则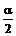 是( ).
是( ).
A.第一或二象限的角 B.第二或三象限的角
C.第一或三象限的角 D.第二或四象限的角
2. 已知过点A(-2,m)和B(m,4)的直线与直线2x+y-1=0平行,则m的值为
A.0 B.-8 C.2 D.10
3.在(x-1)(x+1)8的展开式中x5的系数是( )
A.-14 B.14 C.-28 D.28
4.设三棱柱ABC-A1B1C1的体积是V,P.Q分别是侧棱AA1.CC1上的点,且PA=QC1,则四棱锥B-APQC的体积为( )
A.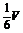 B.
B.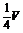 C.
C.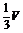 D.
D.
5.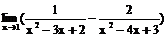 =( )
=( )
A.-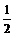 B.
B.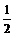 C.-
C.-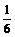 D.
D.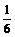
6.若 ,则( )
,则( )
A.a<b<c B.c<b<a C.c<a<b D.b<a<c
7.设0≤x<2π,且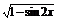 =sinx-cosx, 则( )
=sinx-cosx, 则( )
A.0≤x≤π B.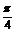 ≤x≤
≤x≤ C.
C.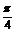 ≤x≤
≤x≤ D.
D.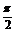 ≤x≤
≤x≤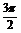
8. ( )
( )
A.tanx B.tan2x
C.1 D.
9.已知双曲线 的焦点为F1.F2,点M在双曲线上且
的焦点为F1.F2,点M在双曲线上且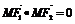 ,则点M到x轴的距离为( )
,则点M到x轴的距离为( )
A.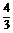 B.
B.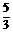 C.
C.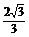 D.
D.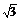
10.设椭圆的两个焦点分别为F1.F2,过F2作椭圆长轴的垂线交椭圆于点P,若三角形F1PF2为等腰直角三角形,则椭圆的离心率为( )
A.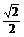 B.
B.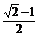 C.
C.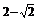 D.
D.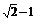
11.不共面的四个定点到平面α的距离都相等,这样的平面α共有( )个
A.3 B.4 C.6 D.7
12.计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号 这些符号与十进制的数的对应关系如下表:
这些符号与十进制的数的对应关系如下表:
|
十六进制 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
十进制 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
例如用十六进制表示:E+D=1B,则A×B=( )
A.6E B.72 C.5F D.B0
13.已知复数z0=3+2i, 复数z满足z z0=3z+z0,则z=
z0=3z+z0,则z=

14.已知向量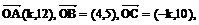 ,且A.B.C三点共线,则k=
.
,且A.B.C三点共线,则k=
.
15.设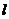 为平面上过点(0,1)的直线,
为平面上过点(0,1)的直线,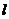 的斜率等可能地取-2
的斜率等可能地取-2 ,-
,- ,-
,-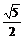 ,0,
,0,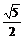 ,
, , 2
, 2 , 用ξ表示坐标原点到
, 用ξ表示坐标原点到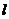 的距离,则随机变量ξ的数学期望Eξ=
的距离,则随机变量ξ的数学期望Eξ=

16.已知在△ABC中,∠ACB=90°,BC=3,AC=4,P是AB上的点,则P到AC.BC距离的的乘积的最大值是

17.(本小题满分12分)
甲.乙.丙三台机器是否需要照顾相互之间没有影响 已知在某一个小时内,甲.乙都需要照顾的概率是0.05,甲.丙都需要照顾的概率是0.05,乙.丙都需要照顾的概率是0.125
已知在某一个小时内,甲.乙都需要照顾的概率是0.05,甲.丙都需要照顾的概率是0.05,乙.丙都需要照顾的概率是0.125
1)求甲.乙.丙三台机器在这一个小时内各自需要照顾的概率?
2)计算在这一个小时内至少有一台需要照顾的概率?
18.(本小题满分12分)
四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,
平面VAD⊥底面ABCD
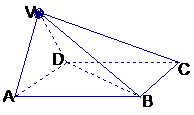 1)求证AB⊥面VAD;
1)求证AB⊥面VAD;
2)求面VAD与面VDB所成的二面角的大小.
19.(本小题满分12分)
 中,内角
中,内角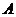 .
.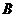 .
.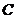 的对边分别为
的对边分别为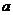 .
. .
.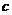 ,已知
,已知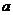 .
. .
.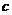 成等比数列,且
成等比数列,且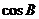


(1)求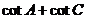 的值;
的值;
(2)若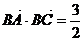 ,求
,求 的值
的值
20.(本小题满分12分)
在等差数列{an}中,公差d≠0,且a2是a1和a4的等比中项,已知a1,a3,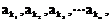 成等比数列,求数列k1,k2,k3,…,kn的通项kn
成等比数列,求数列k1,k2,k3,…,kn的通项kn
21.(本小题满分14分)
设 .
.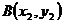 两点在抛物线
两点在抛物线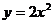 上,
上,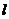 是
是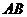 的垂直平分线
的垂直平分线
1)当且仅当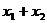 取何值时,直线
取何值时,直线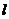 经过抛物线的焦点
经过抛物线的焦点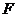 ?证明你的结论;
?证明你的结论;
2)当直线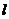 的斜率为2时,求
的斜率为2时,求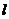 在
在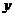 轴上截距的取值范围
轴上截距的取值范围
22.(本小题满分12分)
已知函数f(x)=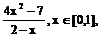
(1)求函数f(x)的单调区间和值域;
(2)设a≥1, 函数g(x)=x3-3a2x-2a, x∈[0,1], 若对于任意x1∈[0,1], 总存在x0∈[0,1], 使得g((x0) =f(x1)成立,求a的取值范围